一、目錄

1. 樣本概述和說明
   
   1. 資料來源
   2. 目標變數的定義
   3. 樣本統計
   4. 資料視覺化
2. 特徵工程
   
   1. 缺失值處理
   2. 同值化處理
   3. 業務相關性
   4. IV值篩選變數
   5. 皮爾森係數
3. 最優分箱
   
   1. 等距分箱
   2. 卡方分箱
4. 模型評估
   
   1. 準確率
   2. 召回率
   3. ROC曲線
   4. KS值
5. 評分卡
6. 模型結果

二、樣本概述和說明

1.資料來源
本文的資料來源從Lending Club官方網站下載
開發資料集：2017.01-2017.06
驗證資料集：2017.07-2017.09

選取的開發資料集共計202234條資料，變數總數為145個，驗證資料集共計122703條資料，變數總數為145個。其145個變數的部分解釋如下：

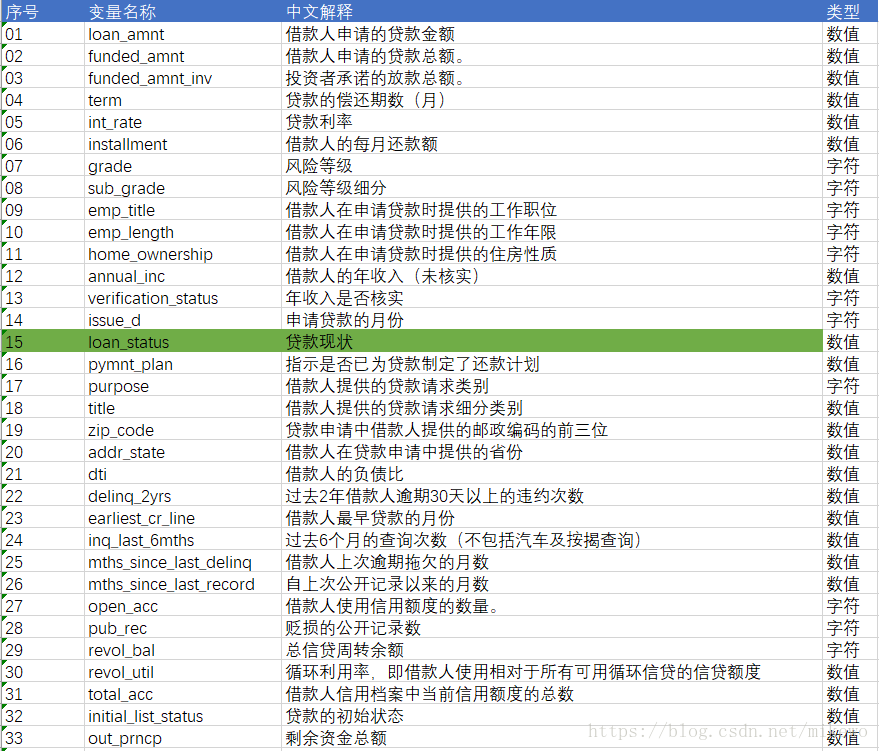
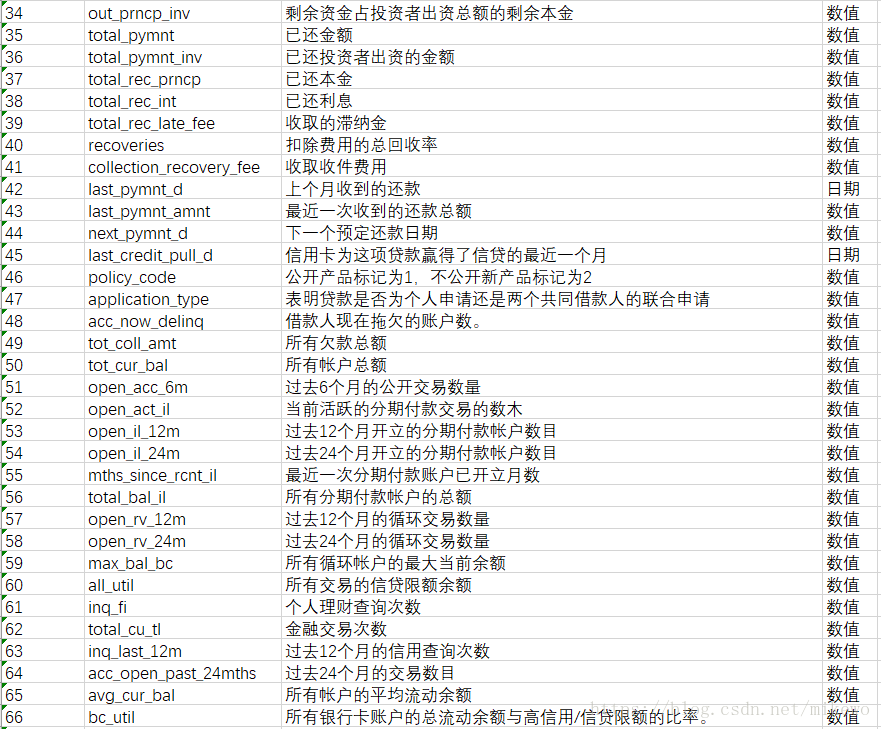
2. 目標變數的定義

在釋義中，綠色標註的就是目標變數，為了方便將其變數名標註為y，其變數名和統計個數如下：

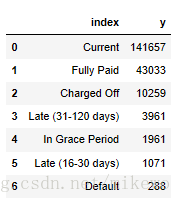
根據業務場景對其進行定義，一般逾期超過30天以上的客戶定義為信用較差的客戶，對於一些客戶無法直接定義其信用的優劣，則將這部分不確定的客戶，定義為信用中等的客戶，具體的定義如下：

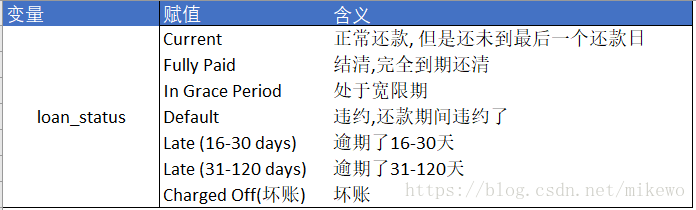
#定義新函式 , 給出目標Y值
def coding(col, codeDict):
    colCoded = pd.Series(col, copy=True)
    for key, value in codeDict.items():
        colCoded.replace(key, value, inplace=True
 
)

    return colCoded
codeDict = {'Current':0,'Fully Paid':0,
     'Late (31-120 days)':1,'Charged Off':1,
     'Late (16-30 days)':2,'In Grace     Period':2,'Default':2}      

3. 樣本統計

表現視窗：在時間軸上從觀察點向後推得的表現視窗，用來提取目標變數和進行表現排除。
觀察視窗：從觀察點向前推一段時間得到觀察視窗，用來提取自變數資訊和進行觀察視窗排除，觀察視窗一般長度通常為6-12個月。

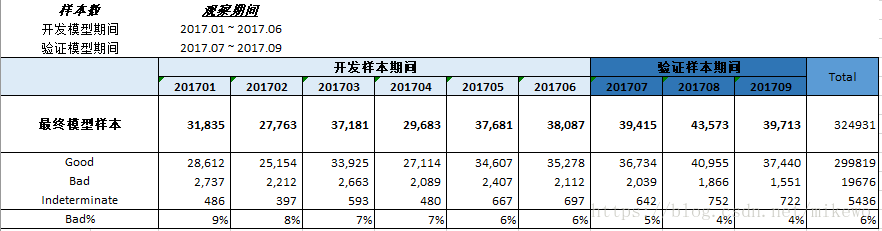
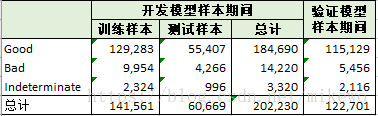
可以看出其特徵值數量過大，需要進行有效的篩選，而且其壞樣本的佔比比較低，僅6-7%，在後續的處理中需要做不平衡樣本處理。
4. 資料視覺化

資料視覺化可以比較直觀的觀察資料，對資料有一個整體的瞭解，在開發樣本中，風險評估（grade）處於B和C的比較多，換言之，申請貸款的人風險評估大多數處於中等偏上。

工作年限大於十年的提交貸款申請的人數遠超過其他工年年限的申請人數。

資料基本符合正太分佈：

三、特徵工程

針對特徵值比較多的資料，需要篩選特徵值，其常用的方法如下：
- 缺失值比率：根據缺失率大小來決定是否刪除該特徵值，一般來說包含太多的缺失值的資料包含有用的資訊可能性很小。
- 同值化處理：根據特徵值的取值的一致程度來決定是否刪除該特徵值，一般來說如果特徵值包含的數值大部分為同一值時，則其有用的資訊可能性很小。
- 高相關過濾：主要是指對於兩列資料變化趨勢相似，包含的資訊相似的情況下，只需要保留其中一列即可。
- 組合演算法降維：主要是利用機器學習的方法，如隨機森鈴等，通過演算法找出資訊量較高的特徵值。
1. 缺失值處理
對於處理值處理，方法有很多，常用的方法如下：
- 對於缺失值佔比比較高的，直接捨棄
- 利用數值0，均值，中位數，眾數等方法填充
- 用上下資料進行填充
- 利用機器學習演算法擬合和預測缺失值

在這裡首先對目標變數缺失的4行進行刪除，再進行缺失值統計，並針對缺失值超多90%的特徵值進行刪除，其中針對缺失值比較少的如il_util（13%）用數值0進行填充，變數數由145個變為102個


2.同值化處理
對於變數的同值性過高時，其包含的有用資訊可能性很小，所以針對這類特徵值進行同值化處理，根據業務情況，其閾值定義為93%，變數數由102個變為85個

3.業務相關性
從業務角度出發刪除一些不相關的資訊，這樣不但可以減少特徵值，還可以有效地保護客戶的資訊，如貸款後的資訊（如last_credit_pull_d），不必要的個人資訊（如），高度重複資訊（sub_grade，風險評估細分），變數數由85個變為62個。

# next_pymnt_d : 客戶下一個還款時間
# emp_title ：資料分類太多，實用性不大
# last_pymnt_d ：最後一個還款日期
# zip_code ：郵政編碼前三位
# last_credit_pull_d ：最近一個貸款的時間
# sub_grade ： 與grade重複，分類太多
# title： title與purpose的資訊基本重複
# issue_d ： 放款時間，申請模型用不上
# earliest_cr_line : 貸款客戶第一筆借款日期
# total_rec_prncp : 已還本金
# total_rec_int :   已還利息
df5 = df4.drop(['emp_title','last_credit_pull_d','sub_grade','title',
                'issue_d','earliest_cr_line','funded_amnt_inv',
                'next_pymnt_d','last_pymnt_amnt','last_pymnt_d',
                'total_rec_prncp', 'out_prncp','out_prncp_inv',
                'total_pymnt','total_pymnt_inv','installment',
                'bc_open_to_buy','percent_bc_gt_75','tot_hi_cred_lim',
                'mths_since_recent_inq','total_bc_limit','zip_code','addr_state'], axis = 1)

4.IV值篩選變數
WOE的全稱是“Weight of Evidence”，即證據權重。WOE是對原始自變數的一種編碼形式。而要對一個變數進行WOE編碼，需要首先把這個變數進行分箱。

P_good 是特徵所在分段內的好樣本數量佔所有好樣本（全部資料中）數量的比例，而 P_bad同理。
woe的含義類似於資訊熵，同時很重要的一點是它對資料進行了歸一化處理，也就是將所有不同特徵劃在了統一的尺度上。

IV值是Information Values的簡稱，他是衡量某一特徵資料中的資訊量的度量單位，如果資訊含量足夠大，則表示其為有價值的特徵。

IV值的預測能力如下：
IV ： < 0.02 ： 無預測能力
IV ：0.02-0.10 ： 預測能力弱
IV ：0.10-0.30 ： 預測能力中
IV ： >0.30 ： 預測能力強
首先利用資料字典將目前62個變數中的object資料型別的變數轉換為數字變數，再採用等距分箱對特徵值進行處理。

mapping_dict = {"grade":
                    {"A": 0,"B": 1,"C": 2, "D": 3, "E": 4,"F": 5,"G": 6},
                "initial_list_status": 
                    {"w": 0,"f": 1,},
                "emp_length": 
                    {"10+ years": 11,"9 years": 10,"8 years": 9,
                     "7 years": 8,"6 years": 7,"5 years": 6,"4 years":5,
                     "3 years": 4,"2 years": 3,"1 year": 2,"< 1 year": 1,
                     "n/a": 0},
                "verification_status":
                    {"Not Verified":0,"Source Verified":1,"Verified":2},
                "purpose":
                    {"credit_card":0,"home_improvement":1,"debt_consolidation":2,       
                     "other":3,"major_purchase":4,"medical":5,"small_business":6,
                     "car":7,"vacation":8,"moving":9, "house":10, 
                     "renewable_energy":11,"wedding":12},
                "home_ownership":
                    {"MORTGAGE":0,"ANY":1,"NONE":2,"OWN":3,"RENT":4}} 
df6 = df5.replace(mapping_dict) 

計算其WOE值和IV值，並刪掉IV<0.02的變數，變數由62個變為29個

def filter_iv(data, group=10):
    iv_value,all_iv_detail = cal_iv(data, group=group)
    ##利用IV值，先刪除掉IV值<0.02的特徵
    '''IV值小於0.02,變數的預測能力太弱'''
    list_value = iv_value[iv_value.ori_IV <= 0.02].var_name
    filter_data = iv_value[['var_name','ori_IV']].drop_duplicates()
    print(filter_data)

    new_list = list(set(list_value))
    print('小於0.02的變數有:',len(new_list))
    print(new_list)
    #new_list.sort(key = list_value.index)   
    drop_list = new_list
    new_data = data.drop(drop_list, axis = 1)
    return new_data, iv_value

5.皮爾森係數
對皮爾森係數繪圖，觀察多重共性的變數，對其進行分析，保留相關性低於閾值0.6的變數，保證其係數都是獨立不相關的。

通過用隨機森林進行擬合，得出特徵的權重，比較保留下了變數，其對照表如下：

四、最優分箱

分箱的方法主要包括等距分箱，等頻分箱，最優分箱等，其優勢在於：

1.離散特徵的增加和減少都很容易，易於模型的快速迭代；
2.稀疏向量內積乘法運算速度快，計算結果方便儲存，容易擴充套件；
3.離散化後的特徵對異常資料有很強的魯棒性；
4.離散化後可以進行特徵交叉，由M+N個變數變為M*N個變數，進一步引入非線性，提升表達能力；
5.特徵離散化以後，起到了簡化了邏輯迴歸模型的作用，降低了模型過擬合的風險。

這裡主要採用的是常規的等距分箱和評分卡中常用的卡方分箱，通過投票的方式得到最優的分箱結果：

五、模型評估

因為在統計樣本的時候提到，該資料的壞樣本佔比為6-7%，資料屬於不平衡樣本，所以訓練模型要對樣本進行處理。對於不平衡樣本的處理方法有很多，比如：
- 欠取樣(從好樣本里面隨機抽取與壞樣本同樣多的資料進行模型擬合,但是拋棄了大資料好樣本的資料，可能會造成較大的偏差)
- 過取樣(將壞樣本反覆抽取並生成與好樣本同樣多的資料進行模型擬合，只是單純的重複了正例，可能會過擬合)
- SMOTE演算法(本質是過取樣，通過在區域性區域進行K-近鄰生成了新的壞樣本，可以理解為是一種整合學習，但是也可能會過擬合)
這裡主要採用的是SMOTE演算法對樣本進行預處理後，匯入到邏輯迴歸模型中，並對模型進行評估，其KS值為24.37%，對於評分卡而言，結果尚可。

             precision    recall  f1-score   support

        0.0       0.65      0.63      0.64    184690
        1.0       0.64      0.66      0.65    184690

avg / total       0.65      0.65      0.65 

The confusion_matrix is:
 [[117264  67426]
 [ 63159 121531]]

accuracy_score 0.646475174617
precision_score 0.643167493133
recall_score 0.658026964102
ROC_AUC is 0.706879521886  

同時也需要檢視模型對標籤的區分度，也就是K-S曲線：

KS需要TPR和FPR兩個值：真正類率(true positive rate ,TPR), 計算公式為TPR=TP/ (TP+ FN)，刻畫的是分類器所識別出的 正例項佔所有正例項的比例。另外一個是假正類率(false positive rate, FPR),計算公式為FPR= FP / (FP + TN)，計算的是分類器錯認為正類的負例項佔所有負例項的比例。KS=max(TPR-FPR)。其中：
TP：真實為1且預測為1的數目
FN：真實為1且預測為0的數目
FP：真實為0的且預測為1的數目
TN：真實為0的且預測為0的數目

K-S score 0.24373544859

六、評分卡

評分卡設定的分值刻度可以通過將分值表示為好壞比率（或者說是概率）的對數線性表示式來定義：

對於信用評分的計算方法如下：

根據以上概念，這裡我們需要提前設定初始變數，也就是Score以及對應的odds，這裡假設初始分值為600分，對應好壞比率為20，好壞比率每翻一番，其分值增加20分，即：

通過代入WOE值，得到評分卡

七、模型結果

根據評分卡計算每個開發樣本的分數，從而得到開發樣本的模型結果，其KS為24.82%，GINI為34.62%，結果尚可。應為驗證樣本沒有參與開發模型，所以利用同樣的操作對驗證樣本進行資料清洗，並得到評分卡，在對每一條資料進行評分，最終得到驗證樣本的模型結果為KS為29.71%，GINI為40.84%。對於申請評分卡而言，說明該模型分類的能力尚可，且開發結果和驗證結果基本一致，說明該模型比較穩定。

評分模型的表現評估。
KS: 用以評估模型對好、壞客戶的判別區分能力，計算累計壞客戶與累計好客戶百分比的最大差距。KS值範圍在0%-100%，判別標準如下：
KS: <20% : 差
KS: 20%-40% : 一般
KS: 41%-50% : 好
KS: 51%-75% : 非常好
KS: >75% : 過高，需要謹慎的驗證模型
GINI: 用以評估模型表現，按照評分大小從小到大對客戶進行排序，計算每個分數段能捕捉到的累計壞客戶百分比。GINI值範圍在0%-100%，判別標準如下：
GINI: <30% : 差
GINI: 30%-40% : 一般
GINI: 41%-50% : 好
GINI: 51%-60% : 非常好
GINI: >60% : 過高，需要謹慎的驗證模型

評分結果在開發樣本中分數呈現正態分佈：

從概率密度函式中，可以好壞客戶一部分是分離的：

評分卡構建時最重要的是特徵工程和分箱邏輯，這兩項需要考慮因素很多，而且對結果的影響因素很大，要謹慎對待。