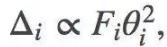編譯 | AI科技大本營

參與 |  劉 暢

編輯 |  明 明

【AI科技大本營導讀】本文介紹了兩篇自動學習神經網路架構方向的最新方法，他們主要是通過計算扔掉一些引數/特徵來實現的。第一篇L0方法看起來像是一個更簡單的優化演算法，第二篇Fisher修剪法論文來自於作者及其實驗室。

第一篇論文：《Christos Louizos, Max Welling, Diederik P. Kingma (2018) Learning Sparse Neural Networks through $L_0$ Regularization》 論文地址

第二篇論文：《Lucas Theis, Iryna Korshunova, Alykhan Tejani, Ferenc Huszár (2018) Faster gaze prediction with dense networks and Fisher pruning》 

第二篇論文的標題中提到的修剪，其含義是在神經網路中減少或控制非零引數的數量，或者是在神經網路中需要用到的特徵圖數量。從更抽象的層面來看，至少有三種方法可以做到這一點，而修剪方法只是其中之一：

• 正則化該方法修改了目標函式/學習問題，因此優化過程中有可能會找到一個帶少量引數的神經網路。Louizos等（2018）做了這方面的工作。
• 修剪該方法是在一個龐大的網路上，刪除在某種程度上冗餘的特徵或引數。（Theis et al，2018）的工作就可以作為一個例子。
• 生長第三種方法知名度比較低，從小型網路開始，按生長標準逐步增加新的單元。

▌為什麼要剪枝？

修剪網路有各種各樣的原因。 最顯然的原因是希望保持相同效能的同時能降低計算成本。而且刪除那些在深度網路中沒有真正使用的特徵，也可以加速推理和訓練過程。你也可以將修剪看作是一種結構探索：即找出在每層中需要多少個特徵才能獲得最佳效能。

第二個原因是通過減少引數數量，也就是減少引數空間中的冗餘，可以實現提升模型的泛化能力。正如我們在近期關於深度網路泛化能力的研究中所看到的那樣，引數的原始數量（L_0  norm）實際上並不能預測其泛化能力。也就是說，根據經驗，我們發現修剪網路有助於提升泛化能力。同時，深度學習社群正在開發新的引數相關量來預測/描述泛化。 Fisher-Rao norm就是一個很好的例子。有趣的是，Fisher修剪（Theis et al，2018）被證明與Fisher-Rao norm之間有很好的相關性，這可能意味著修剪，引數冗餘和泛化之間，有著更深層次的關係。

▌L_0 正則化

我發現Louizos等人（2018年）關於L_0的論文非常有趣，它可以被看作是幾個月前我在機器學習食譜（譯者注：部落格

所以我將這篇文章總結為以下步驟，每個步驟逐步改變著模型優化問題：

1、首先從難以優化的損失函式開始：在常用的損失函式上加上L_0範數，兩者線性組合。 L_0範數簡單的計算了向量中的非零項，它是一個不可微分的常量函式。 所以這是一個非常困難的組合優化問題。

2、應用變分優化方法將不可微的函式轉化為可微函式。這通常是通過在引數$ \ theta $上引入一個概率分佈p_ {\ psi}（\ theta）。即使目標對於任何 \ theta 引數都是不可微的，但是在 p_ {\ psi} 下的平均損失可能是可微的w.r.t.$\$ PSI。為了找到最優\ psi ，通常可以使用一個增強（REINFORCE）梯度估計器，從而得到優化的策略。 但是這種方法通常具有高方差，因此我們會用步驟三的方法。

3、將重構造引數（reparametrization）技巧應用於pψ上，以此構造一個低方差梯度估計器。但是，這隻適用於連續變數。為了處理離散性，我們轉向步驟四。

4、使用concrete relaxation，通過連續近似逼近離散隨機變數。現在我們有一個較低的方差（與REINFORCE相比）梯度估計器，可以通過反向傳播和簡單的蒙特卡羅取樣來計算。 您可以在SGD（Adam）中使用這些梯度，也正是這篇論文做的工作。

有趣的是，步驟3並沒有提到優化策略或變分優化之類的東西。取而代之的出發點是基於不同連線的spike-and-slab先驗。我建議閱讀這篇論文時，可以考慮到這一點。

作者表明這確實在減少引數數量方面起了作用，並且與其他方法相比更有優勢。根據這些步驟，思考從一個問題轉換到另一個問題，讓您也可以概括或改進這個想法。例如，REBAR或RELAX梯度估計器相比其他的估計器，它能夠達到無偏差和低方差的效果，而且這種方法在這個問題上也可以有很好的效果。

▌Fisher修剪法

我想談的第二篇論文是來自我們自己實驗室的。（Theis等人，2018）這篇論文不是純粹的方法，而是關注於具體應用，即如何構建一個快速神經網路來預測影象顯著性。修剪網路的方法來源於在Twitter上裁剪照片的原理。

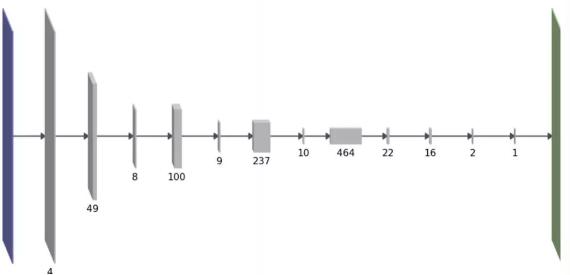
我們的目標也是為了降低網路的計算成本，特別是在遷移學習環境中：當使用預訓練的神經網路開始構建時，您將繼承解決原始任務所需的大量複雜性計算，而這對於解決你的目標任務可能是多餘的。我們的高階（high-level）修剪方法有一個不同之處：與L0範數或組稀疏度不同，我們用一個稍微複雜的公式來直接估計方法的前向計算時間。這個公式是相鄰層間相互作用的每層引數數量的二次函式。有趣的是，這樣做的結果是網路結構是厚層和薄層間的交替運算，如下所示：

我們使用一次去掉一個卷積的特徵圖的方法，來修剪訓練好的網路。選擇下一個待修剪特徵圖的一個原則是儘量減少由此造成的訓練損失增加。從這個原則出發，利用損失函式的二階泰勒展開式，再做出更多的假設，我們能得到下面關於引數θi的修剪關係：

Fi表示Fisher資訊矩陣的第i個對角線值。雖然上面的公式去除了單個引數，但是我們可以延伸到如何去除整個特徵圖。而修剪是通過去除每個迭代中具有最小Δ的引數或特徵對映，並且在迭代間再重新訓練網路來實現的。欲瞭解更多詳情，請參閱論文。

除了論文中提到的內容之外，我想指出一下Fisher修剪法與我之前在這個部落格上討論過的想法之間的一些聯絡。

Fisher-Rao範數

第一個聯絡是Fisher-Rao範數。假設某一分鐘Fisher矩陣資訊是對角的，在理論上這是一個大而且不合理的假設，但是在應用中簡化了它，就得到了能用於實踐的演算法。有了這個假設，θ的Fisher-Rao範數變成：

用這種形式寫下來，你就能看到FR範數與Fisher修剪法之間的聯絡了。根據所使用的Fisher資訊矩陣的特定定義，您可以近似解釋FR範數，如下：

• 當刪除一個隨機引數，訓練日誌可能（Fisher經驗資訊）會按預期下降

• 或者當刪除一個引數，由模型（Fisher模型資訊）定義的條件分佈的近似變化

在現實世界中，Fisher資訊矩陣並不是對角的，這實際上是理解泛化的一個重要方面。首先，只考慮對角線值使Fisher修剪與網路的某些引數（非對角線雅可比矩陣）之間有些聯絡。但是也許在Fisher-Rao範數和引數冗餘之間有更深層次的聯絡。

彈性權重鞏固（Elastic Weight Consolidation）

使用對角Fisher資訊值來指導修剪也與（Kirkpatrick等，2017）提出的彈性權重鞏固有相似之處。在EWC中，Fisher資訊值用於確定哪些權重能夠在解決以前的任務中更重要。而且，雖然演算法是從貝葉斯線上學習中推匯出來的，但是你也可以像Fisher修剪那樣從泰勒展開的角度來決定。

我用來理解和解釋EWC的一個比喻是共享硬碟。（提醒：與其他所有的比喻一樣，這可能完全沒有意義）。神經網路的引數就像是某類硬碟或儲存卷。訓練神經網路的任務過程包括壓縮訓練資料並將資訊儲存到硬碟上。如果你沒有機制來保持資料不被複寫，那麼該硬碟就將被複寫。在神經網路中，災難性遺忘是以同樣的方式發生。EWC就像是一份在多個使用者之間共享硬碟的協議，而使用者不需要複寫其它使用者的資料。 EWC中的Fisher資訊值可以被看作軟體層面的不復寫標誌。在對第一個任務進行訓練之後，我們計算出Fisher資訊值，該值表示該任務的關鍵資訊是由哪些引數儲存的。Fisher值較低的是冗餘的引數，其可以被重複使用並用來儲存新的資訊。在這個比喻中， Fisher資訊值的總和就是衡量了硬碟容量的大小，而修剪實際上就是丟棄了硬碟上不用於儲存任何東西的部分。

總結

在我看來，這兩種方法/論文字身都很有趣。 L0方法看起來像是一個更簡單的優化演算法，可能是Fisher修剪的迭代，一次刪除一個特徵方法更可取。然而，當你在遷移學習中，從一個大的預訓練模式開始時，Fisher修剪則更適用。

作者| FerencHuszár

原文連結