E. Product Sum time limit per test 1 second memory limit per test 256 megabytes input standard input output standard output

Blake is the boss of Kris, however, this doesn't spoil their friendship. They often gather at the bar to talk about intriguing problems about maximising some values. This time the problem is really special.

You are given an array a of length n. The characteristic of this array is the value 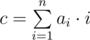 — the sum of the products of the valuesa

i by i. One may perform the following operation exactly once: pick some element of the array and move to any position. In particular, it's allowed to move the element to the beginning or to the end of the array. Also, it's allowed to put it back to the initial position. The goal is to get the array with the maximum possible value of characteristic.

Input

The first line of the input contains a single integer n (2 ≤ n ≤ 200 000) — the size of the array a.

The second line contains n integers ai (1 ≤ i ≤ n, |ai| ≤ 1 000 000) — the elements of the array a.

Output

Print a single integer — the maximum possible value of characteristic of a that can be obtained by performing no more than one move.

Examples input

4
4 3 2 5

output

39

input

5
1 1 2 7 1

output

49

input

3
1 1 2

output

9

Note

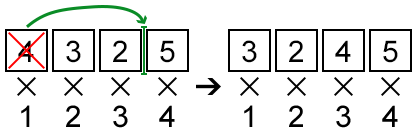
In the first sample, one may pick the first element and place it before the third (before 5). Thus, the answer will be3·1 + 2·2 + 4·3 + 5·4 = 39.

In the second sample, one may pick the fifth element of the array and place it before the third. The answer will be1·1 + 1·2 + 1·3 + 2·4 + 7·5 = 49.

題意是給出n個數，計算sum(i*a[i])i從1到n。然後你可以任意挪動一個數的位置，使得和最大，求和。

感覺是個三分的題，但是我沒學過三分。。。

列舉每一個可能被挪動的元素，然後二分其前後位置，計算每一個位置產生的結果差值，求其最大。自己瞎搞水過的。。。

程式碼：

#pragma warning(disable:4996)
#include <iostream>
#include <functional>
#include <algorithm>
#include <cstring>
#include <vector>
#include <string>
#include <cstdio>
#include <cmath>
#include <queue>
#include <stack>
#include <deque>
#include <set>
#include <map>
using namespace std;
typedef long long ll;

#define INF 0x3fffffffffffffff

const ll mod = 1e9 + 7;
const int maxn = 1e6 + 5;

ll n, sum;
ll val[maxn], pre[maxn];

ll cal(ll pos, ll mid)
{
	ll res;
	if (pos > mid)
	{
		res = (mid - pos)*val[pos] + (pre[pos - 1] - pre[mid - 1]);
	}
	else
	{
		res = (mid - pos)*val[pos] - (pre[mid] - pre[pos]);
	}
	return res;
}

void solve()
{
	ll i, j, k;
	scanf("%I64d", &n);

	sum = 0;
	for (i = 1; i <= n; i++)
	{
		scanf("%I64d", &val[i]);
		sum += i*val[i];
		pre[i] = val[i] + pre[i - 1];
	}
	ll le, ri, mid;
	ll ans = 0;
	for (i = 1; i <= n; i++)
	{
		le = 1, ri = n;
		while (le < ri)
		{
			mid = (le + ri) / 2;
			if (cal(i, mid) >= cal(i, mid + 1))
			{
				ri = mid;
			}
			else
			{
				le = mid + 1;
			}
		}
		ans = max(ans, cal(i, ri));
	}

	for (i = 1; i <= n; i++)
	{
		le = 1, ri = n;
		while (le < ri)
		{
			mid = (le + ri + 1) / 2;
			if (cal(i, mid) >= cal(i, mid - 1))
			{
				le = mid;
			}
			else
			{
				ri = mid - 1;
			}
		}
		ans = max(ans, cal(i, le));
	}
	printf("%I64d", ans + sum);
}

int main()
{

#ifndef ONLINE_JUDGE  
	freopen("i.txt", "r", stdin);
	freopen("o.txt", "w", stdout);
#endif 

	solve();

	return 0;
}