Java集合框架面試問題集錦
Q:最常見的數據結構有哪些,在哪些場景下應用它們?
A. 大部分人都會遺漏樹和圖這兩種數據結構。樹和圖都是很有用的數據結構。如果你在回答中提及到它們的話,面試者可能會對你進行進一步進行的考核。
Q:你如何自己實現List,Set和Map?
A:雖然Java已經提供了這些接口的經過實踐證明和測試過的實現,但是面試者還是喜歡這樣問,來測試你對數據結構的理解。我寫的《Core Java Career Essentials》一書中通過圖例和代碼詳細地講解了這些內容。
數組是最常用的數據結構。數組的特點是長度固定,可以用下標索引,並且所有的元素的類型都是一致的。數組常用的場景有把:從數據庫裏讀取雇員的信息存儲為EmployeeDetail[],把一個字符串轉換並存儲到一個字節數組中便於操作和處理,等等。盡量把數組封裝在一個類裏,防止數據被錯誤的操作弄亂。另外,這一點也適合其他的數據結構。
列表和數組很相似,只不過它的大小可以改變。列表一般都是通過一個固定大小的數組來實現的,並且會在需要的時候自動調整大小。列表裏可以包含重復的元素。常用的場景有,添加一行新的項到訂單列表裏,把所有過期的商品移出商品列表,等等。一般會把列表初始化成一個合適的大小,以減少調整大小的次數。
堆棧只允許對最後插入的元素進行操作(也就是後進先出,Last In First Out – LIFO)。如果你移除了棧頂的元素,那麽你可以操作倒數第二個元素,依次類推。這種後進先出的方式是通過僅有的peek(),push()和pop()這幾個方法的強制性限制達到的。這種結構在很多場景下都非常實用,例如解析像(4+2)*3這樣的數學表達式,把源碼中的方法和異常按照他們出現的順序放到堆棧中,檢查你的代碼看看小括號和花括號是不是匹配的,等等。
這種用堆棧來實現的後進先出(LIFO)的機制在很多地方都非常實用。例如,表達式求值和語法解析,校驗和解析XML,文本編輯器裏的撤銷動作,瀏覽器裏的瀏覽記錄,等等。這裏是一些關於堆棧的一些Java面試題。
這裏是一個用多線程來訪問阻塞隊列的例子。
鏈表是一種由多個節點組成的數據結構,並且每個節點包含有數據以及指向下一個節點的引用,在雙向鏈表裏,還會有一個指向前一個節點的引用。例如,可以用單向鏈表和雙向鏈表來實現堆棧和隊列,因為鏈表的兩端都是可以進行插入和刪除的動作的。當然,也會有在鏈表的中間頻繁插入和刪除節點的場景。Apache的類庫裏提供了一個TreeList的實現,它是鏈表的一個很好的替代,因為它只多占用了一點內存,但是性能比鏈表好很多。也就是說,從這點來看鏈表其實不是一個很好的選擇。
ArrayList是列表的一個很好的實現。相比較TreeList而言,ArrayList在除了在列表中間插入或者刪除元素的情況,其他操作都比TreeList快很多。TreeList的實現是在內部使用了一個樹形的結構來保證所有的插入和刪除動作的復雜度都是O(log n)的。這種實現方式使得TreeList在頻繁插入和刪除元素的時候的性能遠遠高於ArrayList和LinkedList。
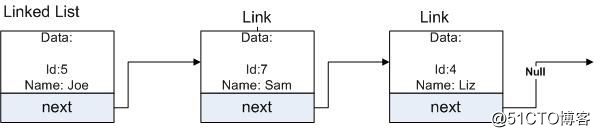
class Link {
private int id; // data
private String name; // data
private Link next; // reference to next link
}
HashMap的訪問時間接近穩定,它是一種鍵值對映射的數據結構。這個數據結構是通過數組來實現的。它通過hash函數來給元素定位,並且用沖突檢測算法來處理被hash到同一位置的值。例如,保存雇員的信息可以用雇員的id來作為key,對從properties文件裏讀入的屬性-屬性值可以用key/value對來保存,等等。HashMap在初始化的時候,給定一個合適的大小可以減少調整大小的次數。
樹是一種由節點組成的數據結構,每個節點都包含數據元素,並且有一個或多個子節點,每個子節點指向一個父節點(譯者註:除了根節點)可以表示層級關系或者數據元素的順序關系。常用的場景有表示一個組織裏的雇員層級關系,XML元素的層級關系,等等。如果樹的每個子節點最多有兩個葉子節點,那麽這種樹被稱為二叉樹。二叉樹是一種非常常用的樹形結構, 因為它的這種結構使得節點的插入和刪除都非常高效。樹的邊表示從一個節點到另外一個節點的快捷路徑。
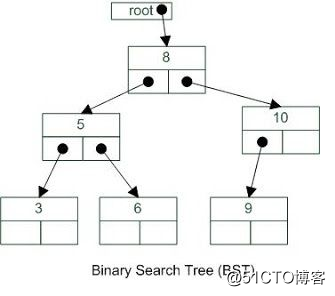
Java裏面沒有直接提供樹的實現,但是它很容易通過下面的方式來實現。只需要創建一個Node對象,裏面包含一個指向葉子節點的ArrayList。
package bigo;
import java.util.ArrayList;
import java.util.List;
public class Node {
private String name;
private List<node> children = new ArrayList<node>( );
private Node parent;
public Node getParent( ) {
return parent;
}
public void setParent(Node parent) {
this.parent = parent;
}
public Node(String name) {
this.name = name;
}
public void addChild(Node child) {
children.add(child);
}
public void removeChild(Node child) {
children.remove(child);
}
public String toString( ) {
return name;
}
}
只要數據元素的關系可以表示成節點和邊的網狀結構的話,就可以用圖來表示。樹是一種特殊的圖,它的所有節點都只能有一個父節點。和樹不同的是,圖的形狀是由實際問題或者問題的抽象來決定的。例如,圖中節點(或者頂點)可以表示不同的城市,而圖的邊則可以表示兩個城市之間的航線。
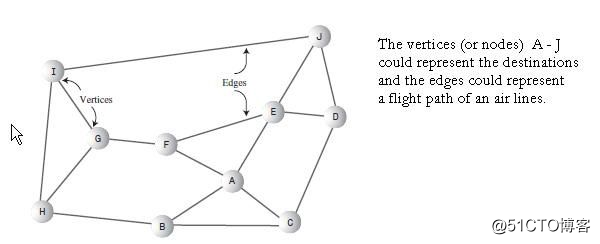
在Java裏構造一個圖,你需要解決數據通過什麽方式保存和訪問的問題。在圖裏面也會用到上面提到的數據結構。Java的API裏沒有提供圖的實現。不過有很多第三方庫裏提供了,例如JUNG,JGraphT,以及JDSL(不過好像不支持泛型)。《Core Java Career Essential》一書包含了用Java實現的可用示例。
Q:你對大O這個符號有什麽了解呢,你是否可以根據不同的數據結構舉出一些列子來?
A:大O符號可以表示一個算法的效率,也可以用來描述當數據元素增加時,最壞情況下的算法的性能。大O符號也可以用來衡量的性能,例如內存消耗量。有時候你可能會為了減少內存使用量而選擇一個比較慢的算法。大O符號可以表示在大量數據的情況下程序的性能。不過,對於程序在大量數據量下的性能的測量,唯一比較實際的方式是行用較大的數據集來進行性能基準測試,這樣可以把一些在大O復雜度分析裏沒有考慮到的情況包含進去,例如在虛擬內存使用比較多的時候系統會發生換頁的情況。雖然基準測試比大O符號表示的結果更加實際,但是它不適用於設計階段,所以在這個這時候大O復雜度分析是最合適的選擇。
各種數據結構在搜索,插入和刪除算法上的性能都可以用下面方式表示:常量復雜度O(1),線性復雜度O(n),對數復雜度O(log n),指數復雜度O(c^n),多項式復雜度O(n^c),平方復雜度O(n^2)以及階乘復雜度O(n!),這裏面的n都指的是數據結構裏的元素的數量。性能和內存占用是可以相互權衡的。下面是一些示例。
示例1:在HashMap裏查找一個元素的的時間復雜度是常量的,也即是O(1)。這是因為查找元素使用的是哈希函數,並且計算一個哈希值的時間是不受HashMap裏的元素的個數的影響的。
示例2:線性搜索一個數組,列表以及鏈表都是的復雜度線性的,也即是O(n),這是查找的時候需要遍歷整個列表。也就是說,如果一個列表的長度是原來的兩倍,那麽搜索所花的時間也是原來的兩倍。
示例3:一個需要比較數組裏的所有元素的排序算法的復雜度是多項式的,即是O(n^2)。這是因為一個嵌套的for循環的復雜度是O(n^2)。在搜素算法裏有這樣的例子。
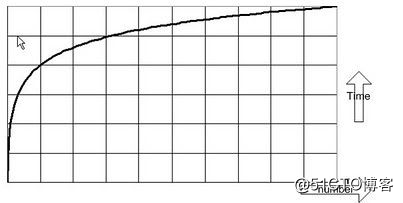
示例4:二分搜索一個數組或者數組列表的復雜度是對數的,即是O(log n)。在鏈表裏查詢一個節點的復雜度一般是O(n)。相比較數組鏈表和數組的O(log n)的性能而言,隨著元素數量的增長,鏈表的O(n)的復雜度的性能就比較差了。對數的時間復雜度就是如果10個元素花費的時間是x單位的話,100個元素最多花費2x單位的時間,而10000個元素最多花費4x個單位的時間。如果你在一個平面坐標上畫出圖形的話,你會發現時間的增長沒有n(元素的個數)快。
Q:HashMap和TreeMap在性能上有什麽樣的差別呢?你比較傾向於使用哪一個?
A:一個平衡樹的性能是O(logn)。Java裏的TreeMap用一個紅黑樹來保證key/value的排序。紅黑樹是平衡二叉樹。保證二叉樹的平衡性,使得插入,刪除和查找都比較快,時間復雜度都是O(log n)。不過它沒有HashMap快,HashMap的時間復雜度是O(1),但是TreeMap的優點在於它裏面鍵值是排過序的,這樣就提供了一些其他的很有用的功能。
Q:怎麽去選擇該使用哪一個呢?
A:使用無序的HashSet和HashMap,還是使用有序的TreeSet和TreeMap,主要取決於你的實際使用場景,一定程度上還和數據的大小以及運行環境有關。比較實際的一個原因是,如果插入和更新都比較頻繁的話,那麽保證元素的有序可以提高快速和頻繁查找的性能。如果對於排序操作(例如產生一個報表合作者運行一個批處理程序)的要求不是很頻繁的話,那麽把數據以無序的方式存儲,然後在需要排序的時候用Collections.sort(…)來進行排序,會比用有序的方式來存儲可能會更加高效。這個只是一種可選的方式,沒人能給你一個確切的答案。即使是復雜度的理論,例如O(n),成立的前提也是在n足夠大的情況下。只要在n足夠小的情況下,就算是O(n)的算法也可能會比O(log n)的算法更加高效。另外,一個算法可能在AMD處理器上的速度比在Intel處理器上快。如果你的系統有交換區的話,那麽你還要考慮磁盤的性能。唯一可以確定的性能測試途徑是用大小合適的數據來測試和衡量程序的性能和內存使用量。在你所選擇的硬件上來測試這兩種指標,是最合適的方法。
Q:如何權衡是用無序的數組還是有序的數組呢?
A:有序數組最大的優點在於n比較大的時候,搜索元素所花的時間O(log n)比無序素組所需要的時間O(n)要少很多。有序數組的缺點在於插入的時間開銷比較大(一般是O(n)),因為所有比插入元素大的值都要往後移動。而無序數組的插入時間開銷是常量時間,也就是說,插入的速度和元素的數量無關。下面的代碼片段展示了向有序數組和無序數組插入元素。
插入元素到一個無序的數組裏
package bigo;
import java.util.Arrays;
public class InsertingElementsToArray {
public static void insertUnsortedArray(String toInsert) {
String[ ] unsortedArray = { "A", "D", "C" };
String[ ] newUnsortedArray = new String[unsortedArray.length + 1];
System.arraycopy(unsortedArray, 0, newUnsortedArray, 0, 3);
newUnsortedArray[newUnsortedArray.length - 1] = toInsert;
System.out.println(Arrays.toString(newUnsortedArray));
}
public static void main(String[ ] args) {
insertUnsortedArray("B");
}
}
插入元素到一個有序數組
package bigo;
import java.util.Arrays;
public class InsertingElementsToArray {
public static void insertSortedArray(String toInsert) {
String[ ] sortedArray = { "A", "C", "D" };
/*
- Binary search returns the index of the search item
- if found, otherwise returns the minus insertion point. This example
- returns index = -2, which means the elemnt is not found and needs to
-
be inserted as a second element.
*/
int index = Arrays.binarySearch(sortedArray, toInsert);if (index < 0) { // not found.
// array indices are zero based. -2 index means insertion point of
// -(-2)-1 = 1, so insertIndex = 1
int insertIndex = -index - 1;String[ ] newSortedArray = new String[sortedArray.length + 1];
System.arraycopy(sortedArray, 0, newSortedArray, 0, insertIndex);
System.arraycopy(sortedArray, insertIndex,
newSortedArray, insertIndex + 1, sortedArray.length - insertIndex);
newSortedArray[insertIndex] = toInsert;
System.out.println(Arrays.toString(newSortedArray));
}
}public static void main(String[ ] args) {
insertSortedArray("B");
}
}
所以,如何去選擇還是取決於實際的使用情況。你需要考慮下面幾個問題。你的程序是插入/刪除的操作多,還是查找的操作多?數組裏最多可能存儲多少元素?排序的頻率是多少?以及你的性能基準測試的結果是怎樣的?
Q:怎麽實現一個不可變集合?
A:這個功能在Collections類裏實現了,它通過裝飾模式實現了對一般集合的封裝。
public class ReadOnlyExample {
public static void main(String args[ ]) {
Set<string> set = new HashSet<string>( );
set.add("Java");
set.add("JEE");
set.add("Spring");
set.add("Hibernate");
set = Collections.unmodifiableSet(set);
set.add("Ajax"); // not allowed.
}
}
Q:下面的代碼的功能是什麽呢?其中的LinkedHashSet能用HashSet來取代嗎?
import java.util.ArrayList;
import java.util.LinkedHashSet;
import java.util.List;
public class CollectionFunction {
public <e> List<e> function (List <e> list) {
return new ArrayList<e>(new LinkedHashSet<e>(list));
}
}
A:上面的代碼代碼通過把原有列表傳入一個LinkedHashSet來去除重復的元素。在這個情況裏,LinkedHashSet可以保持元素原來的順序。如果這個順序是不需要的話,那麽上面的LinkedHashSet可以用HashSet來替換。
Q:Java集合框架都有哪些最佳實踐呢?
A:根據實際的使用情況選擇合適的數據結構,例如固定大小的還是需要增加大小的,有重復元素的還是沒有的,需要保持有序還是不需要,遍歷是正向的還是雙向的,插入是在末尾的還是任意位置的,更多的插入還是更多的讀取,是否需要並行訪問,是否允許修改,元素類型是相同的還是不同的,等等。另外,還需要盡早考慮多線程,原子性,內存使用量以及性能等因素。
不要假設你的集合裏元素的數量一直會保持較小,它也有可能隨著時間增長。所以,你的集合最好能夠給定一個合適的大小。
針對接口編程優於針對實現編程。例如,可能在某些情況下,LinkedList是最佳的選擇,但是後來ArrayList可能因為性能的原因變得更加合適
不好的方式:
1ArrayList list = new ArrayList(100);
好的方式:
// program to interface so that the implementation can change
List list = new ArrayList(100);
List list2 = new LinkedList(100);
List emptyList = Collections.emptyList( );
Set emptySet = Collections.emptySet( );
在取得列表的時候,如果返回的結果是空的話,最好返回一個長度為0的集合或者數組,而不要返回null。因為,返回null的話可能能會導致程序錯誤。調用你的方法的開發人員可能會忘記對返回為null的情況進行處理。
封裝好集合:一般來說,集合都是不可變的對象。所以盡量不要把集合的成員變量暴露給調用者。因為他們的操作一般都不會進行必要的校驗。
Java集合框架面試問題集錦
