3、相機引數評估

3.1 原理

相機引數的評估也稱為相機定標。要想理解這部分內容，首先應該從成像原理開始講起。

圖6 小孔成像原理

從圖6可以看出，真實物體通過小孔對映到成像平面上，小孔到成像平面的距離稱為焦距f。在成像平面上的影象是映象倒立的，所以為了研究方便，在小孔和物體之間定義一個虛擬成像平面（在後面，我們把該平面也稱為成像平面），它與小孔的距離也為焦距，則兩個成像平面的影象大小是相同的，但虛擬成像平面上的影象與原物體的方向是一樣的。

圖7 成像的幾何模型

我們以小孔為座標原點建立一個三維直角座標系XYZ（如圖7所示），座標原點C稱為相機的光心。成像平面xy平行於XY，並且距離光心C

由幾何知識可得：

（31）

式中，λ＝Z/f，則x＝fX/Z，y＝fY/Z。因此空間中Q點的三維座標對映到成像平面的二維座標q點在齊次座標下的線性對映關係為：

（32）

如圖7所示，在成像平面（座標系為xy）的座標原點為P，但影象（設座標系為uv）的座標原點一般在左上角，所以這兩個座標系之間需要通過平移來進行轉換。另外成像平面xy是長度單位，而相機影象感測器的單位是畫素，因此畫素與長度之間也是需要轉換的，而且水平和垂直的畫素往往是不相同的，所以橫縱軸的轉換系數是不一致。因此式32改寫為：

（33）

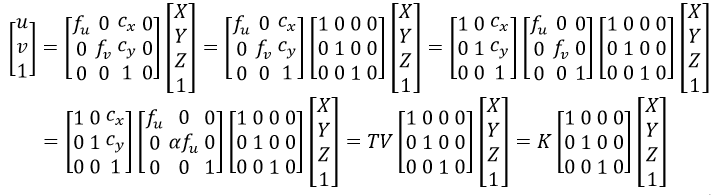
式中，f_u和f_v為焦距f在橫縱軸的長度和畫素的轉換，它們之間的關係可以寫為f_v＝αf_u，(c_x, c_y)為座標平移。因為矩陣K的引數都是基於相機內部自身的引數，因此K稱為相機內參數，K＝TV。

相機除了具有內參數外，還有外引數。式33中的(X, Y, Z)稱為相機座標，而它與真實的世界座標(X’, Y’, Z’)還存在歐幾里得變換，即：

（34）

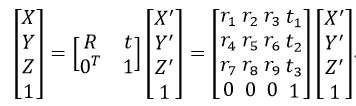
式中，R為3×3的旋轉矩陣，t為3×1的平移向量。式34代入式33，得

（35）

式中，[R|t]稱為相機外引數，M稱為投影矩陣。

如果得到的兩幅影象如圖3所示的那樣，即相機在三角架上通過旋轉得到的兩幅影象，則對於同一個世界座標上的點(X

（36）

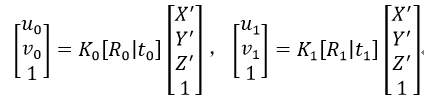
由於相機只做旋轉處理（或者我們認為物體離相機很遠），則t₀＝t₁＝0，從而得到(u₀, v₀)和(u₁, v₁)的關係為：

（37）

式中，R₁₀為由影象1到影象0的相對旋轉矩陣，R₁₀＝R₁R₀^-1。由式2可得：

（38）

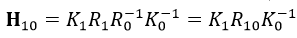
為簡單起見，我們設兩幅影象的相機內參數中的座標平移都為0，即K＝V，因為拋棄引數T對影象拼接影響不大。

我們在評估焦距時，還需定義f_1u＝f_1v＝f₁，f_0u＝f_0v＝f₀，即設影象的長寬等畫素：

（39）

則式38表示為

（40）

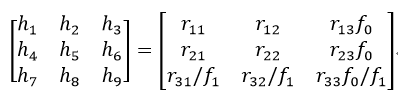
式中，R₁₀＝[r_ij]。

由式40我們就可以得到焦距f₀和f₁：觀察矩陣R₁₀可知，R₁₀前兩行一定有相同的範數，並且是正交的，因此

（41）

（42）

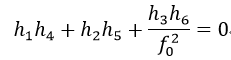
由式41可得：

（43）

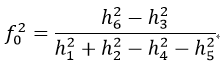
由式42可得：

（44）

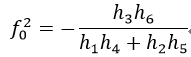
由式43和式44得到了兩個f₀，選取哪個呢？比較式43和式44中分母部分的絕對值的大小，如果式43的分母大，則選擇分式大的值作為f₀，否則如果式44的分母大，則選擇值小的作為f₀。

同理，矩陣R₁₀的前兩列也一定有相同的範數，並且也是正交的，因此

（45）

（46）

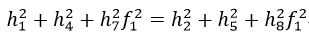
由式45可得

（47）

由式46可得

（48）

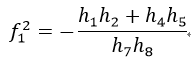
比較式47和式48中分母部分的絕對值的大小，如果式48的分母大，則選擇分式大的值作為f₁，否則如果式47的分母大，則選擇值小的作為f₁。

如果兩幅影象的焦距相同，則最終這兩幅影象的焦距f為：

（49）

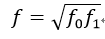
當評估計算得到多個f時，可取這些f的中值作為所有相機的焦距。

焦距得到後，我們就可以由式38得到R₁₀：

（50）

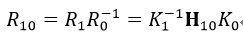
則R₀₁（由影象0到影象1的相對旋轉矩陣）為：

（51）

則

（52）

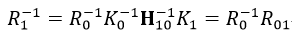
對於剛性物體，它的旋轉都是沿笛卡爾座標系的x軸、y軸和z軸旋轉，則分別沿著這三個軸的旋轉矩陣定義為：

（53）

則旋轉矩陣R表示為：

（54）

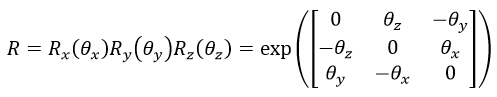
三維旋轉除了可以用旋轉矩陣描述外，還可以用旋轉向量r描述，即r＝[r_x, r_y, r_z]^T。旋轉向量的長度（模）表示繞軸逆時針旋轉的角度θ。旋轉向量和旋轉矩陣可以通過Rodrigues演算法進行轉換。由旋轉向量轉換為旋轉矩陣的Rodrigues演算法描述如下：

（55）

（56）

（57）

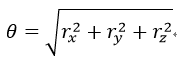
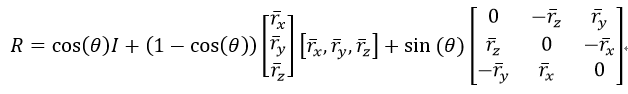
式中，I為3×3的單位矩陣。而由旋轉矩陣轉換為旋轉向量的Rodrigues演算法公式為：

（58）

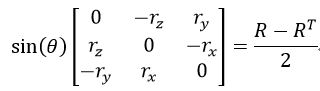
當有多幅影象需要拼接為一幅影象時，是要以其中一幅影象為基準，其他影象都要旋轉到該基準影象平面上的，所以就需要找到基準平面。這裡用到的演算法為最大生成樹演算法。

待拼接影象的排列是無序的，而且我們事先是不知道它們之間的關係的，我們只知道它們之間的單應矩陣，而單應矩陣是由影象間的內點計算評估得到的。由此我們可以構造一個無向圖G，G的節點為影象，G的邊為內點數，然後利用並查集在該G中得到一棵最大生成樹。

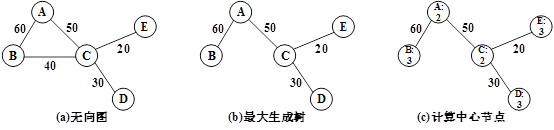
圖8 最大生成樹

圖8為用於拼接的最大生成樹的一個例子，圖(a)為無向圖，節點為影象（A、B、C、D、E），節點間的邊為內點數。圖(b)為最大生成樹，由影象C到影象B要經過最大的邊連線，所以要經過影象A，而影象C和影象B之間的連線就需要去掉了。

我們把樹的中心節點作為基準影象。中心節點的確定方法為：計算每一個節點到所有葉節點的距離，把其中的最大值作為該節點的值；然後選擇這些值中最小者作為中心節點。這裡的距離指的是節點間的節點數。如圖8(c)所示，節點A和C為中心節點。中心節點可能是1個，也可能是2個，如果是2個，則選擇其中一個即可。

基於以上方法，我們得到了相機的內外引數，但這樣得到的引數忽略了多個影象間的約束，而且會產生累計誤差。這時，我們就需要用到光束平差法（Bundle Adjustment）來精確化相機引數。光束指的是相機光心“發射”出來的光束（或射線），它透過相片達到物點，因此相片中的點應該和物點處於一個光束線上，但當兩者不共線時，我們就需要對結構和視角引數進行調節，以達到最優解甚至共線的目的。最優化一般採用前文介紹過的LM演算法。

應用於光束平差法的LM演算法，誤差指標函式可以有兩個，一個是重對映誤差，另一個是射線發散誤差。

重對映誤差公式為式25（即一個內點要有x軸和y軸兩個誤差值），而單應矩陣H是由式38得到。也就是說H是由相機的內外引數得到。相機的內外引數一共有7個：f_u、α、c_x、c_y、r_x、r_y和r_z。前4個引數是內參數（見式33），後3個引數是外引數（即式55中的旋轉向量的三個元素）。因此式25中的h為h(f_u, α, c_x, c_y, r_x, r_y,r_z)，由此得到J(h)為：

（59）

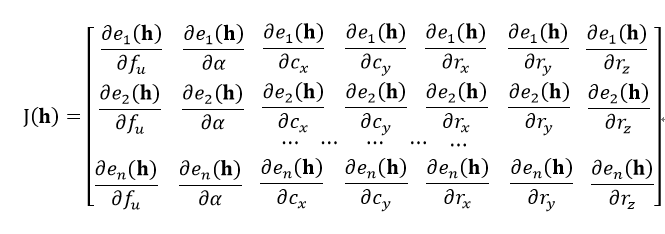
式中，n表示待拼接的影象數量，也就是所有的相機。有時為了計算方便，導數可以用差分近似，例如我們要計算e對f_u的偏導，則

（60）

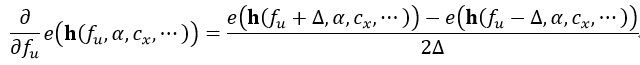
式中，∆表示一個很小的數。

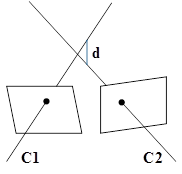
圖9 射線發散概念

第二種誤差指標函式是基於射線發散原理。如圖9所示，不同的相機發出的射線透過相片後達到同一個物點，但由於誤差，兩條射線不會相交，或者稱為兩條射線發散了，我們就把這兩條射線間的最短距離d定義為射線發散誤差。

下面，我們不加證明的給出射線發散誤差的計算公式：

設(u₁, v₁, 1)和(u₂, v₂, 1)為兩幅不同影象的同一特徵點的齊次座標，則由單應矩陣H₁和H₂分別得到它們的物點座標為：

（61）

分別對座標進行歸一化處理：

（62）

（63）

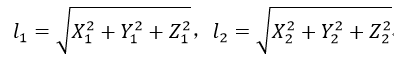
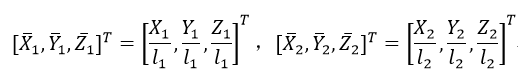
為了簡化計算，射線間的最短距離可以表示為基於不同焦距f₁和f₂下的歸一化後的物點座標之差：

（64）

式64說明在計算射線發散誤差時，每一個內點有x軸、y軸和z軸三個誤差值。

我們假設射線就是相機的光軸，因此單應矩陣H中的引數α＝1，c_x＝c_y＝0，所以式25中h只是基於4個引數的變數，即h(f_u, r_x,r_y, r_z)，由此得到射線發散誤差的J(h)為：

（65）

前面介紹的光束平差法會引起波形效應，即拼接的影象會呈現蛇形分佈，這是因為真實拍攝相片時不大可能都保持水平而不傾斜的，也就是重力軸沒有垂直於影象。因此我們就需要引入一個全域性校正矩陣Q，用於“拉直”拼接影象，該方法也成為波形校正。

校正的目的應該是，在第k個相機旋轉矩陣R_k乘以Q後，全域性y軸應該與影象的x軸垂直，這種約束條件可以表示為：

（66）

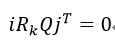
式中，i＝(1, 0, 0)，j＝(0, 1, 0)，該式的含義是R_k的第一行r_k0垂直於Q的第二列q₁。式66的這類約束問題可以看成是最小二乘問題：

（67）

因此，q₁是矩量矩陣∑r^Tr的最小特徵值所對應的特徵向量。矩陣Q的其他列的經驗公式為：

（68）

式中，×表示矩陣的點乘（即對應元素相乘，與MATLAB中的點乘相同），分母表示對分子取模，即q₀是歸一化的結果。

（69）

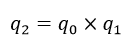
最終的全域性校正矩陣Q＝[q₀q₁q₂]，而用Q乘以各個相機的R即實現了波形校正。如果要進行垂直校正拉直，則需選擇最大特徵值對應的特徵向量。

3.2 原始碼

Estimator類是相機引數評估器的基類，HomographyBasedEstimator和BundleAdjusterBase都是Estimator類的子類。HomographyBasedEstimator類主要負責相機引數的計算評估，BundleAdjusterBase類主要通過光束平差法使相機引數精確化。

我們先來看HomographyBasedEstimator類，它的主要內容就是estimate函式：

void HomographyBasedEstimator::estimate(const vector<ImageFeatures> &features, const vector<MatchesInfo> &pairwise_matches,
                                        vector<CameraParams> &cameras)
//features表示所有待拼接影象的特徵
//pairwise_matches表示匹配點對
//cameras表示相機引數資訊
{
    LOGLN("Estimating rotations...");
#if ENABLE_LOG
    int64 t = getTickCount();
#endif

    const int num_images = static_cast<int>(features.size());    //得到待拼接影象的數量

#if 0
    // Robustly estimate focal length from rotating cameras
    vector<Mat> Hs;
    for (int iter = 0; iter < 100; ++iter)
    {
        int len = 2 + rand()%(pairwise_matches.size() - 1);
        vector<int> subset;
        selectRandomSubset(len, pairwise_matches.size(), subset);
        Hs.clear();
        for (size_t i = 0; i < subset.size(); ++i)
            if (!pairwise_matches[subset[i]].H.empty())
                Hs.push_back(pairwise_matches[subset[i]].H);
        Mat_<double> K;
        if (Hs.size() >= 2)
        {
            if (calibrateRotatingCamera(Hs, K))
                cin.get();
        }
    }
#endif
    //is_focals_estimated_為HomographyBasedEstimator類的全域性變數，表示是否需要進行焦距評估
    if (!is_focals_estimated_)    //需要焦距評估，因為焦距還沒有被評估
    {
        // Estimate focal length and set it for all cameras
        vector<double> focals;    //表示所有影象的焦距
        //評估焦距，estimateFocal在後面給出詳細介紹
        estimateFocal(features, pairwise_matches, focals);
        cameras.assign(num_images, CameraParams());    //為相機引數分配空間
        for (int i = 0; i < num_images; ++i)
            cameras[i].focal = focals[i];    //相機焦距賦值
    }
    else    //不需要焦距評估
    {
        //得到相機內參數的cx, cy
        for (int i = 0; i < num_images; ++i)
        {
            cameras[i].ppx -= 0.5 * features[i].img_size.width;
            cameras[i].ppy -= 0.5 * features[i].img_size.height;
        }
    }

    // Restore global motion
    Graph span_tree;    //定義最大生成樹
    vector<int> span_tree_centers;    //表示最大生成樹的中心節點
    //得到最大生成樹，該函式在後面給出了詳細的介紹
    findMaxSpanningTree(num_images, pairwise_matches, span_tree, span_tree_centers);
    //以中心節點的影象為基準，計算其他影象與該影象的旋轉矩陣，CalcRotation結構體在後面給出了詳細的介紹
    span_tree.walkBreadthFirst(span_tree_centers[0], CalcRotation(num_images, pairwise_matches, cameras));

    // As calculations were performed under assumption that p.p. is in image center
    for (int i = 0; i < num_images; ++i)    //得到相機引數中的座標平移
    {
        cameras[i].ppx += 0.5 * features[i].img_size.width;
        cameras[i].ppy += 0.5 * features[i].img_size.height;
    }

    LOGLN("Estimating rotations, time: " << ((getTickCount() - t) / getTickFrequency()) << " sec");
}

評估相機焦距：

void estimateFocal(const vector<ImageFeatures> &features, const vector<MatchesInfo> &pairwise_matches,
                       vector<double> &focals)
//features表示影象的特徵
//pairwise_matches表示匹配點對
//focals表示相機焦距
{
    const int num_images = static_cast<int>(features.size());    //待拼接的影象數量
    focals.resize(num_images);    //定義focals向量變數的長度

    vector<double> all_focals;    //表示焦距
    //巢狀迴圈，得到每兩個影象之間的匹配資訊
    for (int i = 0; i < num_images; ++i)
    {
        for (int j = 0; j < num_images; ++j)
        {
            //得到第i幅影象與第j幅影象之間的匹配資訊
            const MatchesInfo &m = pairwise_matches[i*num_images + j];
            if (m.H.empty())    //沒有單應矩陣，說明它們之間不能拼接
                continue;    //進入下一個迴圈
            double f0, f1;    //表示這兩幅影象的焦距
            bool f0ok, f1ok;    //表示是否得到了這兩幅影象的焦距
            //從單應矩陣中得到焦距，focalsFromHomography函式在後面給出介紹
            focalsFromHomography(m.H, f0, f1, f0ok, f1ok);
            if (f0ok && f1ok)    //得到了兩幅影象的焦距
                all_focals.push_back(sqrt(f0 * f1));    //式49，把焦距存入all_focals內
        }
    }

    if (static_cast<int>(all_focals.size()) >= num_images - 1)
    {
        double median;    //表示焦距中值

        std::sort(all_focals.begin(), all_focals.end());    //所有焦距排序
        //得到所有焦距的中值，作為最終的焦距
        if (all_focals.size() % 2 == 1)
            median = all_focals[all_focals.size() / 2];
        else
            median = (all_focals[all_focals.size() / 2 - 1] + all_focals[all_focals.size() / 2]) * 0.5;

        for (int i = 0; i < num_images; ++i)    //為所有相機的焦距賦同樣的值
            focals[i] = median;    //焦距賦值
    }
    //按照正常的方面沒有得到焦距的處理方法：焦距為所有拼接影象的長寬之和的平均值
    else
    {
        LOGLN("Can't estimate focal length, will use naive approach");
        double focals_sum = 0;
        for (int i = 0; i < num_images; ++i)    //所有影象的長寬之和
            focals_sum += features[i].img_size.width + features[i].img_size.height;
        for (int i = 0; i < num_images; ++i)
            focals[i] = focals_sum / num_images;    //平均值
    }
}

從單應矩陣中得到焦距：

void focalsFromHomography(const Mat& H, double &f0, double &f1, bool &f0_ok, bool &f1_ok)
//H表示單應矩陣
//f0和f1分別表示單應矩陣H所轉換的兩幅影象的焦距
//f0_ok和f1_ok分別表示f0和f1是否評估正確
{
    //確保H的資料型別和格式正確
    CV_Assert(H.type() == CV_64F && H.size() == Size(3, 3));

    const double* h = reinterpret_cast<const double*>(H.data);    //賦值指標
    //分別表示式43和式44，或式47和式48的分母
    double d1, d2; // Denominators
    //分別表示式43和式44，或式47和式48
    double v1, v2; // Focal squares value candidates

    f1_ok = true;
    d1 = h[6] * h[7];    //式48的分母
    d2 = (h[7] - h[6]) * (h[7] + h[6]);    //式47的分母
    v1 = -(h[0] * h[1] + h[3] * h[4]) / d1;    //式48
    v2 = (h[0] * h[0] + h[3] * h[3] - h[1] * h[1] - h[4] * h[4]) / d2;    //式47
    if (v1 < v2) std::swap(v1, v2);    //使v1不小於v2
    //表示到底選取式47還是式48作為f1
    if (v1 > 0 && v2 > 0) f1 = sqrt(std::abs(d1) > std::abs(d2) ? v1 : v2);
    else if (v1 > 0) f1 = sqrt(v1);    //v2小於0，則f1一定是v1的平方根
    else f1_ok = false;    //v1和v2都小於0，則沒有得到f1

    f0_ok = true;
    d1 = h[0] * h[3] + h[1] * h[4];    //式44的分母
    d2 = h[0] * h[0] + h[1] * h[1] - h[3] * h[3] - h[4] * h[4];    //式43的分母
    v1 = -h[2] * h[5] / d1;    //式44
    v2 = (h[5] * h[5] - h[2] * h[2]) / d2;    //式43
    if (v1 < v2) std::swap(v1, v2);    //使v1不小於v2
    //表示到底選取式44還是式43作為f0
    if (v1 > 0 && v2 > 0) f0 = sqrt(std::abs(d1) > std::abs(d2) ? v1 : v2);
    else if (v1 > 0) f0 = sqrt(v1);    //v2小於0，則f1一定是v1的開根號
    else f0_ok = false;    //v1和v2都小於0，則沒有得到f1
}

構建最大生成樹：

void findMaxSpanningTree(int num_images, const vector<MatchesInfo> &pairwise_matches,
                             Graph &span_tree, vector<int> ¢ers)
//num_images表示待拼接影象的數量，也是最大生成樹的節點數
//pairwise_matches表示影象間的拼接資訊
//span_tree表示最大生成樹
//centers表示最大生成樹的中心節點
{
    Graph graph(num_images);    //定義無向圖G
    vector<GraphEdge> edges;    //定義無向圖G的邊

    // Construct images graph and remember its edges
    //遍歷待拼接影象，得到無向圖G的邊，即內點數
    for (int i = 0; i < num_images; ++i)
    {
        for (int j = 0; j < num_images; ++j)
        {
            //如果影象i和j沒有單應矩陣，則說明這兩幅影象不重疊，不能拼接
            if (pairwise_matches[i * num_images + j].H.empty())
                continue;
            //得到影象i和j的內點數
            float conf = static_cast<float>(pairwise_matches[i * num_images + j].num_inliers);
            graph.addEdge(i, j, conf);    //為G新增邊
            edges.push_back(GraphEdge(i, j, conf));    //新增到邊佇列中
        }
    }

    DisjointSets comps(num_images);    //例項化DisjointSets類，表示定義一個並查集
    span_tree.create(num_images);    //建立生成樹
    //表示生成樹的冪，即節點間的連線數，例如某節點的冪為3，說明該節點與其他3個節點相連線
    vector<int> span_tree_powers(num_images, 0);

    // Find maximum spanning tree
    //按無向圖G的邊的大小（內點數）從小到大排序
    sort(edges.begin(), edges.end(), greater<GraphEdge>());
    for (size_t i = 0; i < edges.size(); ++i)    //從小到大遍歷無向圖G的邊
    {
        int comp1 = comps.findSetByElem(edges[i].from);    //得到該邊的起始節點的集合
        int comp2 = comps.findSetByElem(edges[i].to);    //得到該邊的終止節點的集合
        //兩種不相等，說明是一個新的邊，需要通過並查集新增到生成樹中
        if (comp1 != comp2) 
        {
            comps.mergeSets(comp1, comp2);    //合併這兩個節點
            //為生成樹新增該邊
            span_tree.addEdge(edges[i].from, edges[i].to, edges[i].weight);
            span_tree.addEdge(edges[i].to, edges[i].from, edges[i].weight);
            //節點冪的累加
            span_tree_powers[edges[i].from]++;
            span_tree_powers[edges[i].to]++;
        }
    }

    // Find spanning tree leafs
    vector<int> span_tree_leafs;    //表示生成樹的葉節點
    //生成樹的節點的冪為1，則為葉節點
    for (int i = 0; i < num_images; ++i)    //遍歷影象
        if (span_tree_powers[i] == 1)    //表示該影象為葉節點
            span_tree_leafs.push_back(i);    //放入佇列中

    // Find maximum distance from each spanning tree vertex
    vector<int> max_dists(num_images, 0);    //表示節點與葉節點的最大距離
    vector<int> cur_dists;    //表示節點與葉節點的當前距離
    for (size_t i = 0; i < span_tree_leafs.size(); ++i)    //遍歷葉節點
    {
        cur_dists.assign(num_images, 0);    //初始化
        //得到該葉節點到其他節點的距離，IncDistance表示距離的累加，即節點的累計
        span_tree.walkBreadthFirst(span_tree_leafs[i], IncDistance(cur_dists));
        //遍歷所有節點，更新節點到葉節點的最大距離
        for (int j = 0; j < num_images; ++j) 
            max_dists[j] = max(max_dists[j], cur_dists[j]);
    }

    // Find min-max distance
    int min_max_dist = max_dists[0];    //表示所有最大距離中的最小值
    for (int i = 1; i < num_images; ++i)    //遍歷所有節點
        if (min_max_dist > max_dists[i])
            min_max_dist = max_dists[i];    //得到最大距離中的最小值

    // Find spanning tree centers
    centers.clear();    //表示中心節點，清零
    for (int i = 0; i < num_images; ++i)    //遍歷所有節點
        if (max_dists[i] == min_max_dist)
            centers.push_back(i);    //儲存最大距離中的最小值所對應的節點
    //確保中心節點的數量必須大於0並小於3
    CV_Assert(centers.size() > 0 && centers.size() <= 2);
}

計算旋轉矩陣：

struct CalcRotation
{
    CalcRotation(int _num_images, const vector<MatchesInfo> &_pairwise_matches, vector<CameraParams> &_cameras)
        : num_images(_num_images), pairwise_matches(&_pairwise_matches[0]), cameras(&_cameras[0]) {}

    void operator ()(const GraphEdge &edge)
    {
        int pair_idx = edge.from * num_images + edge.to;    //表示匹配點對的索引
        //構造式51中的引數K0
        Mat_<double> K_from = Mat::eye(3, 3, CV_64F);    //初始化
        K_from(0,0) = cameras[edge.from].focal;    //表示式33的fu
        //表示式33的fv
        K_from(1,1) = cameras[edge.from].focal * cameras[edge.from].aspect;
        K_from(0,2) = cameras[edge.from].ppx;    //表示式33的cx
        K_from(1,2) = cameras[edge.from].ppy;    //表示式33的cy
        //構造式51中的引數K1
        Mat_<double> K_to = Mat::eye(3, 3, CV_64F);    //初始化
        K_to(0,0) = cameras[edge.to].focal;    //表示式33的fu
        K_to(1,1) = cameras[edge.to].focal * cameras[edge.to].aspect;    //表示式33的fv
        K_to(0,2) = cameras[edge.to].ppx;    //表示式33的cx
        K_to(1,2) = cameras[edge.to].ppy;    //表示式33的cy

        Mat R = K_from.inv() * pairwise_matches[pair_idx].H.inv() * K_to;    //式51
        //式52，可見CameraParams變數中R實際儲存的是相機旋轉矩陣變數的逆
        cameras[edge.to].R = cameras[edge.from].R * R;
    }

    int num_images;    //表示待拼接影象的數量
    const MatchesInfo* pairwise_matches;    //表示匹配影象的資訊
    CameraParams* cameras;    //表示相機引數
};

下面我們給出BundleAdjusterBase類的講解。BundleAdjusterBase類的建構函式的主要作用是為每個相機引數數量（num_params_per_cam，如果是重對映誤差，則num_params_per_cam應為7，如果是射線發散誤差，則num_params_per_cam應為4）和每個內點誤差數量（num_errs_per_measurement，如果是重對映誤差，則num_errs_per_measurement應為2，即x軸和y軸的誤差，如果是射線發散誤差，則num_errs_per_measurement應為3，即x軸、y軸和z軸的誤差）賦值，並且初始化setRefinementMask（表示需要精確化的相機內參數矩陣K的掩碼矩陣）、setConfThresh（表示內點閾值conf_thresh_，也稱作置信度閾值），以及setTermCriteria（表示LM演算法的迭代終止條件）。

BundleAdjusterBase類的一個重要函式是estimate，它的作用是細化相機引數：

void BundleAdjusterBase::estimate(const vector<ImageFeatures> &features,
                                  const vector<MatchesInfo> &pairwise_matches,
                                  vector<CameraParams> &cameras)
//features表示影象特徵
//pairwise_matches表示影象匹配資訊
//cameras表示相機引數
{
    LOG_CHAT("Bundle adjustment");
#if ENABLE_LOG
    int64 t = getTickCount();
#endif

    num_images_ = static_cast<int>(features.size());    //表示待拼接影象的數量
    features_ = &features[0];    //影象特徵變數的首地址賦值
    pairwise_matches_ = &pairwise_matches[0];    //表示匹配資訊變數的首地址指標
    //初始化LM演算法所需的引數，setUpInitialCameraParams為虛擬函式，實際是呼叫BundleAdjusterBase類的子類
    setUpInitialCameraParams(cameras);

    // Leave only consistent image pairs
    edges_.clear();    //edges_表示影象間內點數，該變數先清零
    //只保留那些內點數大於置信度閾值的影象匹配對
    for (int i = 0; i < num_images_ - 1; ++i)
    {
        for (int j = i + 1; j < num_images_; ++j)
        {
            //得到影象i和影象j的匹配資訊
            const MatchesInfo& matches_info = pairwise_matches_[i * num_images_ + j];
            if (matches_info.confidence > conf_thresh_)    //內點數大於閾值
                edges_.push_back(make_pair(i, j));    //保留這個影象匹配對
        }
    }

    // Compute number of correspondences
    total_num_matches_ = 0;    //total_num_matches_表示所有保留下來的內點數
    for (size_t i = 0; i < edges_.size(); ++i)    //遍歷影象匹配對，計算total_num_matches_
        total_num_matches_ += static_cast<int>(pairwise_matches[edges_[i].first * num_images_ +
                                                                edges_[i].second].num_inliers);
    //例項化CvLevMarq類，表示LM演算法，CvLevMarq類建構函式的第一個引數表示需要優化變數的數量；CvLevMarq類建構函式的第二個引數表示誤差數量；CvLevMarq類建構函式的第三個引數表示LM演算法的迭代終止條件
    CvLevMarq solver(num_images_ * num_params_per_cam_,
                     total_num_matches_ * num_errs_per_measurement_,
                     term_criteria_);

    Mat err, jac;    //err表示LM演算法的誤差，jac表示雅可比引數
    CvMat matParams = cam_params_;    //表示相機引數矩陣
    cvCopy(&matParams, solver.param);    //複製，初始化用於LM演算法的相機引數

    int iter = 0;    //表示迭代次數
    for(;;)    //LM演算法的迭代迴圈
    {
        const CvMat* _param = 0;    //表示LM演算法計算得到的相機引數
        CvMat* _jac = 0;    //表示LM計算得到的雅可比引數
        CvMat* _err = 0;    //表示LM計算得到的誤差
        //呼叫update函式，得到相機引數_param，即式27和式28
        bool proceed = solver.update(_param, _jac, _err);

        cvCopy(_param, &matParams);    //複製，得到相機引數

        if (!proceed || !_err)    //如果該次迭代不成功，或誤差為0
            break;    //退出LM演算法
        //如果_jac不為零，則說明下次迴圈時，solver.update函式需要雅可比引數
        if (_jac) 
        {
            calcJacobian(jac);    //計算雅可比引數，該函式為虛擬函式
            CvMat tmp = jac;
            cvCopy(&tmp, _jac);    //複製
        }
        //如果_err不為零，則說明下次迴圈時，solver.update函式需要誤差引數
        if (_err)
        {
            calcError(err);    //計算誤差，該函式為虛擬函式
            LOG_CHAT(".");
            iter++;    //累計迭代次數
            CvMat tmp = err;
            cvCopy(&tmp, _err);    //複製
        }
    }
    //終端輸出資訊
    LOGLN_CHAT("");
    LOGLN_CHAT("Bundle adjustment, final RMS error: " << sqrt(err.dot(err) / total_num_matches_));
    LOGLN_CHAT("Bundle adjustment, iterations done: " << iter);
    //LM演算法結束後，得到最終的精確的相機引數，該函式為虛擬函式
    obtainRefinedCameraParams(cameras);

    // Normalize motion to center image
    //利用精確的相機引數，再次計算基於中心影象的其他影象的相對旋轉矩陣
    Graph span_tree;
    vector<int> span_tree_centers;
    //利用最大生成樹演算法計算中心影象
    findMaxSpanningTree(num_images_, pairwise_matches, span_tree, span_tree_centers);
    //前面我們介紹過，相機旋轉矩陣CameraParams.R在前面的程式中其實是旋轉矩陣的逆矩陣，現在讓CameraParams.R是基於中心影象的相對旋轉矩陣
    Mat R_inv = cameras[span_tree_centers[0]].R.inv();    //中心影象的旋轉矩陣
    for (int i = 0; i < num_images_; ++i)    //得到其他影象的相對旋轉矩陣
        cameras[i].R = R_inv * cameras[i].R;
    //終端輸出資訊
    LOGLN_CHAT("Bundle adjustment, time: " << ((getTickCount() - t) / getTickFrequency()) << " sec");
}

BundleAdjusterBase類有兩個子類——BundleAdjusterReproj和BundleAdjusterRay，它們分別表示光束平差法的兩個實現方法——重對映方法和射線發散方法，也就是誤差指標函式的兩種形式。

下面我們先給出BundleAdjusterReproj類。setUpInitialCameraParams函式表示初始化相機引數，即在LM演算法迭代之前，要賦予相機引數初值：

void BundleAdjusterReproj::setUpInitialCameraParams(const vector<CameraParams> &cameras)
//cameras表示相機引數的初始化值
{
    //定義表示待精確化的所有引數的矩陣大小
    cam_params_.create(num_images_ * 7, 1, CV_64F);
    SVD svd;
    //遍歷所有的影象（即所有相機），初始化相機引數
    for (int i = 0; i < num_images_; ++i) 
    {
        cam_params_.at<double>(i * 7, 0) = cameras[i].focal;    //初始化fu
        cam_params_.at<double>(i * 7 + 1, 0) = cameras[i].ppx;    //初始化cx
        cam_params_.at<double>(i * 7 + 2, 0) = cameras[i].ppy;    //初始化cy
        cam_params_.at<double>(i * 7 + 3, 0) = cameras[i].aspect;    //初始化α
        //表示得到滿足正交關係的旋轉矩陣R
        svd(cameras[i].R, SVD::FULL_UV);
        Mat R = svd.u * svd.vt;
        if (determinant(R) < 0)
            R *= -1;

        Mat rvec;
        Rodrigues(R, rvec);    //旋轉矩陣R由Rodrigues演算法得到旋轉向量rvec
        CV_Assert(rvec.type() == CV_32F);
        cam_params_.at<double>(i * 7 + 4, 0) = rvec.at<float>(0, 0);    //初始化rx
        cam_params_.at<double>(i * 7 + 5, 0) = rvec.at<float>(1, 0);    //初始化ry
        cam_params_.at<double>(i * 7 + 6, 0) = rvec.at<float>(2, 0);    //初始化rz
    }
}

obtainRefinedCameraParams函式表示得到最終的精確的相機引數：

void BundleAdjusterReproj::obtainRefinedCameraParams(vector<CameraParams> &cameras) const
//cameras表示最終得到的相機引數
{
    for (int i = 0; i < num_images_; ++i)    //遍歷所有的影象（即所有相機），得到相機引數
    {
        cameras[i].focal = cam_params_.at<double>(i * 7, 0);    //得到fu
        cameras[i].ppx = cam_params_.at<double>(i * 7 + 1, 0);   //得到cx
        cameras[i].ppy = cam_params_.at<double>(i * 7 + 2, 0);    //得到cy
        cameras[i].aspect = cam_params_.at<double>(i * 7 + 3, 0);    //得到α

        Mat rvec(3, 1, CV_64F);
        rvec.at<double>(0, 0) = cam_params_.at<double>(i * 7 + 4, 0);    //得到rx
        rvec.at<double>(1, 0) = cam_params_.at<double>(i * 7 + 5, 0);    //得到ry
        rvec.at<double>(2, 0) = cam_params_.at<double>(i * 7 + 6, 0);    //得到rz
        Rodrigues(rvec, cameras[i].R);    //旋轉向量rvec由Rodrigues演算法得到旋轉矩陣R

        Mat tmp;
        cameras[i].R.convertTo(tmp, CV_32F);    //變換資料型別
        cameras[i].R = tmp;    //賦值
    }
}

calcError函式用於計算誤差，即式25：

void BundleAdjusterReproj::calcError(Mat &err)
//err表示計算得到的誤差
{
    err.create(total_num_matches_ * 2, 1, CV_64F);    //定義誤差矩陣

    int match_idx = 0;    //表示重對映誤差的索引
    //遍歷最大生成樹的邊
    for (size_t edge_idx = 0; edge_idx < edges_.size(); ++edge_idx)
    {
        int i = edges_[edge_idx].first;    //表示邊的始端影象
        int j = edges_[edge_idx].second;    //表示邊的終端影象
        double f1 = cam_params_.at<double>(i * 7, 0);    //始端影象的fu
        double f2 = cam_params_.at<double>(j * 7, 0);    //終端影象的fu
        double ppx1 = cam_params_.at<double>(i * 7 + 1, 0);    //始端影象的cx
        double ppx2 = cam_params_.at<double>(j * 7 + 1, 0);    //終端影象的cx
        double ppy1 = cam_params_.at<double>(i * 7 + 2, 0);    //始端影象的cy
        double ppy2 = cam_params_.at<double>(j * 7 + 2, 0);    //終端影象的cy
        double a1 = cam_params_.at<double>(i * 7 + 3, 0);    //始端影象的α
        double a2 = cam_params_.at<double>(j * 7 + 3, 0);    //終端影象的α

        double R1[9];
        Mat R1_(3, 3, CV_64F, R1);
        Mat rvec(3, 1, CV_64F);
        rvec.at<double>(0, 0) = cam_params_.at<double>(i * 7 + 4, 0);    //始端影象的rx
        rvec.at<double>(1, 0) = cam_params_.at<double>(i * 7 + 5, 0);    //始端影象的ry
        rvec.at<double>(2, 0) = cam_params_.at<double>(i * 7 + 6, 0);    //始端影象的rz
        //旋轉向量rvec由Rodrigues演算法得到始端影象的旋轉矩陣R
        Rodrigues(rvec, R1_);

        double R2[9];
        Mat R2_(3, 3, CV_64F, R2);
        rvec.at<double>(0, 0) = cam_params_.at<double>(j * 7 + 4, 0);    //終端影象的rx
        rvec.at<double>(1, 0) = cam_params_.at<double>(j * 7 + 5, 0);    //終端影象的ry
        rvec.at<double>(2, 0) = cam_params_.at<double>(j * 7 + 6, 0);    //終端影象的rz
        //旋轉向量rvec由Rodrigues演算法得到終端影象的旋轉矩陣R
        Rodrigues(rvec, R2_);

        const ImageFeatures& features1 = features_[i];    //得到始端影象的特徵
        const ImageFeatures& features2 = features_[j];    //得到終端影象的特徵
        //得到兩者的影象匹配資訊
        const MatchesInfo& matches_info = pairwise_matches_[i * num_images_ + j];
        //為始端影象的相機內參數矩陣K賦值
        Mat_<double> K1 = Mat::eye(3, 3, CV_64F);
        K1(0,0) = f1; K1(0,2) = ppx1;
        K1(1,1) = f1*a1; K1(1,2) = ppy1;
        //為終端影象的相機內參數矩陣K賦值
        Mat_<double> K2 = Mat::eye(3, 3, CV_64F);
        K2(0,0) = f2; K2(0,2) = ppx2;
        K2(1,1) = f2*a2; K2(1,2) = ppy2;
        //得到兩者的相對單應矩陣H，式38
        Mat_<double> H = K2 * R2_.inv() * R1_ * K1.inv();

        for (size_t k = 0; k < matches_info.matches.size(); ++k)    //遍歷匹配點對
        {
            if (!matches_info.inliers_mask[k])    //表示不是內點
                continue;

            const DMatch& m = matches_info.matches[k];    //表示內點資訊
            //表示內點點對
            Point2f p1 = features1.keypoints[m.queryIdx].pt; 
            Point2f p2 = features2.keypoints[m.trainIdx].pt;
            //由單應矩陣得到p1點的三維空間座標
            double x = H(0,0)*p1.x + H(0,1)*p1.y + H(0,2);
            double y = H(1,0)*p1.x + H(1,1)*p1.y + H(1,2);
            double z = H(2,0)*p1.x + H(2,1)*p1.y + H(2,2);
            //把p1點的三維空間座標重新對映到p2點所在平面，並比較兩者的差，即重對映誤差
            err.at<double>(2 * match_idx, 0) = p2.x - x/z;
            err.at<double>(2 * match_idx + 1, 0) = p2.y - y/z;
            match_idx++;    //累加匹配索引值
        }
    }
}

calcJacobian函式用於計算雅可比矩陣，即式59：

void BundleAdjusterReproj::calcJacobian(Mat &jac)
//jac表示得到的雅可比矩陣
{
    //定義雅可比矩陣的大小
    jac.create(total_num_matches_ * 2, num_images_ * 7, CV_64F);
    jac.setTo(0);    //清零

    double val;
    const double step = 1e-4;    //表示步長，即式60中的∆

    for (int i = 0; i < num_images_; ++i)    //遍歷所有的匹配影象，即式59的所有行
    {
        if (refinement_mask_.at<uchar>(0, 0))    //計算雅可比矩陣的fu項
        {
            val = cam_params_.at<double>(i * 7, 0);    //提取fu
            cam_params_.at<double>(i * 7, 0) = val - step;    //fu－∆
            calcError(err1_);    //計算因fu變換而引起的誤差
            cam_params_.at<double>(i * 7, 0) = val + step;    //fu＋∆
            calcError(err2_);    //計算因fu變換而引起的誤差
            calcDeriv(err1_, err2_, 2 * step, jac.col(i * 7));    //式60
            cam_params_.at<double>(i * 7, 0) = val;    //重新賦值fu，以備其他引數計算
        }
        if (refinement_mask_.at<uchar>(0, 2))    //計算雅可比矩陣的cx項
        {
            val = cam_params_.at<double>(i * 7 + 1, 0);    //提取cx
            cam_params_.at<double>(i * 7 + 1, 0) = val - step;    //cx－∆
            calcError(err1_);    //計算因cx變換而引起的誤差
            cam_params_.at<double>(i * 7 + 1, 0) = val + step;    //cx＋∆
            calcError(err2_);    //計算因cx變換而引起的誤差
            calcDeriv(err1_, err2_, 2 * step, jac.col(i * 7 + 1));    //式60
            cam_params_.at<double>(i * 7 + 1, 0) = val;    //重新賦值cx，以備其他引數計算
        }
        if (refinement_mask_.at<uchar>(1, 2))    //計算雅可比矩陣的cy項
        {
            val = cam_params_.at<double>(i * 7 + 2, 0);    //提取cy
            cam_params_.at<double>(i * 7 + 2, 0) = val - step;    //cy－∆
            calcError(err1_);    //計算因cy變換而引起的誤差
            cam_params_.at<double>(i * 7 + 2, 0) = val + step;    //cy＋∆
            calcError(err2_);    //計算因cy變換而引起的誤差
            calcDeriv(err1_, err2_, 2 * step, jac.col(i * 7 + 2));    //式60
            cam_params_.at<double>(i * 7 + 2, 0) = val;    //重新賦值cy，以備其他引數計算
        }
        if (refinement_mask_.at<uchar>(1, 1))    //計算雅可比矩陣的α項
        {
            val = cam_params_.at<double>(i * 7 + 3, 0);    //提取α
            cam_params_.at<double>(i * 7 + 3, 0) = val - step;    //α－∆
            calcError(err1_);    //計算因α變換而引起的誤差
            cam_params_.at<double>(i * 7 + 3, 0) = val + step;    //α＋∆
            calcError(err2_);    //計算因α變換而引起的誤差
            calcDeriv(err1_, err2_, 2 * step, jac.col(i * 7 + 3));    //式60
            cam_params_.at<double>(i * 7 + 3, 0) = val;    //重新賦值α，以備其他引數計算
        }
        for (int j = 4; j < 7; ++j)    //計算rx, ry, rz
        {
            val = cam_params_.at<double>(i * 7 + j, 0);
            cam_params_.at<double>(i * 7 + j, 0) = val - step;
            calcError(err1_);
            cam_params_.at<double>(i * 7 + j, 0) = val + step;
            calcError(err2_);
            calcDeriv(err1_, err2_, 2 * step, jac.col(i * 7 + j));
            cam_params_.at<double>(i * 7 + j, 0) = val;
        }
    }
}

下面我們先給出BundleAdjusterRay類：

void BundleAdjusterRay::setUpInitialCameraParams(const vector<CameraParams> &cameras)
{
    //定義表示待精確化的所有引數的矩陣大小
    cam_params_.create(num_images_ * 4, 1, CV_64F);
    SVD svd;
    //遍歷所有的影象（即所有相機），初始化相機引數
    for (int i = 0; i < num_images_; ++i)
    {
        cam_params_.at<double>(i * 4, 0) = cameras[i].focal;    //初始化fu
        //表示得到滿足正交關係的旋轉矩陣R
        svd(cameras[i].R, SVD::FULL_UV);
        Mat R = svd.u * svd.vt;
        if (determinant(R) < 0)
            R *= -1;

        Mat rvec;
        Rodrigues(R, rvec);    //旋轉矩陣R由Rodrigues演算法得到旋轉向量rvec
        CV_Assert(rvec.type() == CV_32F);
        cam_params_.at<double>(i * 4 + 1, 0) = rvec.at<float>(0, 0);    //初始化rx
        cam_params_.at<double>(i * 4 + 2, 0) = rvec.at<float>(1, 0);    //初始化ry
        cam_params_.at<double>(i * 4 + 3, 0) = rvec.at<float>(2, 0);    //初始化rz
    }
}

void BundleAdjusterRay::obtainRefinedCameraParams(vector<CameraParams> &cameras) const
{
    for (int i = 0; i < num_images_; ++i)    //遍歷所有的影象（即所有相機），得到相機引數
    {
        cameras[i].focal = cam_params_.at<double>(i * 4, 0);    //得到fu

        Mat rvec(3, 1, CV_64F);
        rvec.at<double>(0, 0) = cam_params_.at<double>(i * 4 + 1, 0);    //得到rx
        rvec.at<double>(1, 0) = cam_params_.at<double>(i * 4 + 2, 0);    //得到ry
        rvec.at<double>(2, 0) = cam_params_.at<double>(i * 4 + 3, 0);    //得到rz
        Rodrigues(rvec, cameras[i].R);    //旋轉向量rvec由Rodrigues演算法得到旋轉矩陣R

        Mat tmp;
        cameras[i].R.convertTo(tmp, CV_32F);    //變換資料型別
        cameras[i].R = tmp;    //賦值
    }
}

void BundleAdjusterRay::calcError(Mat &err)
{
    err.create(total_num_matches_ * 3, 1, CV_64F);    //定義誤差矩陣

    int match_idx = 0;    //表示重對映誤差的索引
    //遍歷最大生成樹的邊
    for (size_t edge_idx = 0; edge_idx < edges_.size(); ++edge_idx)
    {
        int i = edges_[edge_idx].first;    //表示邊的始端影象
        int j = edges_[edge_idx].second;    //表示邊的終端影象
        double f1 = cam_params_.at<double>(i * 4, 0);    //始端影象的fu
        double f2 = cam_params_.at<double>(j * 4, 0);    //終端影象的fu

        double R1[9];
        Mat R1_(3, 3, CV_64F, R1);
        Mat rvec(3, 1, CV_64F);
        rvec.at<double>(0, 0) = cam_params_.at<double>(i * 4 + 1, 0);    //始端影象的rx
        rvec.at<double>(1, 0) = cam_params_.at<double>(i * 4 + 2, 0);    //始端影象的ry
        rvec.at<double>(2, 0) = cam_params_.at<double>(i * 4 + 3, 0);    //始端影象的rz
        //旋轉向量rvec由Rodrigues演算法得到始端影象的旋轉矩陣R
        Rodrigues(rvec, R1_);

        double R2[9];
        Mat R2_(3, 3, CV_64F, R2);
        rvec.at<double>(0, 0) = cam_params_.at<double>(j * 4 + 1, 0);    //終端影象的rx
        rvec.at<double>(1, 0) = cam_params_.at<double>(j * 4 + 2, 0);    //終端影象的ry
        rvec.at<double>(2, 0) = cam_params_.at<double>(j * 4 + 3, 0);    //終端影象的rz
        //旋轉向量rvec由Rodrigues演算法得到終端影象的旋轉矩陣R
        Rodrigues(rvec, R2_);

        const ImageFeatures& features1 = features_[i];    //得到始端影象的特徵
        const ImageFeatures& features2 = features_[j];    //得到終端影象的特徵
        //得到兩者的影象匹配資訊
        const MatchesInfo& matches_info = pairwise_matches_[i * num_images_ + j];
        //為始端影象的相機內參數矩陣K賦值
        Mat_<double> K1 = Mat::eye(3, 3, CV_64F);
        K1(0,0) = f1; K1(0,2) = features1.img_size.width * 0.5;
        K1(1,1) = f1; K1(1,2) = features1.img_size.height * 0.5;
        //為終端影象的相機內參數矩陣K賦值
        Mat_<double> K2 = Mat::eye(3, 3, CV_64F);
        K2(0,0) = f2; K2(0,2) = features2.img_size.width * 0.5;
        K2(1,1) = f2; K2(1,2) = features2.img_size.height * 0.5;
        //計算兩個單應矩陣
        Mat_<double> H1 = R1_ * K1.inv();
        Mat_<double> H2 = R2_ * K2.inv();

        for (size_t k = 0; k < matches_info.matches.size(); ++k)    //遍歷匹配點對
        {
            if (!matches_info.inliers_mask[k])    //表示不是內點
                continue;

            const DMatch& m = matches_info.matches[k];    //表示內點資訊

            Point2f p1 = features1.keypoints[m.queryIdx].pt;    //表示內點的一個點
            //由單應矩陣得到p1點的三維空間座標
            double x1 = H1(0,0)*p1.x + H1(0,1)*p1.y + H1(0,2);
            double y1 = H1(1,0)*p1.x + H1(1,1)*p1.y + H1(1,2);
            double z1 = H1(2,0)*p1.x + H1(2,1)*p1.y + H1(2,2);
            double len = sqrt(x1*x1 + y1*y1 + z1*z1);    //式62
            x1 /= len; y1 /= len; z1 /= len;    //式63

            Point2f p2 = features2.keypoints[m.trainIdx].pt;    //表示內點的另一個點
            //由單應矩陣得到p2點的三維空間座標
            double x2 = H2(0,0)*p2.x + H2(0,1)*p2.y + H2(0,2);
            double y2 = H2(1,0)*p2.x + H2(1,1)*p2.y + H2(1,2);
            double z2 = H2(2,0)*p2.x + H2(2,1)*p2.y + H2(2,2);
            len = sqrt(x2*x2 + y2*y2 + z2*z2);    //式62
            x2 /= len; y2 /= len; z2 /= len;    //式63

            double mult = sqrt(f1 * f2);    //式64的根號內的部分
            //式64
            err.at<double>(3 * match_idx, 0) = mult * (x1 - x2);
            err.at<double>(3 * match_idx + 1, 0) = mult * (y1 - y2);
            err.at<double>(3 * match_idx + 2, 0) = mult * (z1 - z2);

            match_idx++;    //累計
        }
    }
}

void BundleAdjusterRay::calcJacobian(Mat &jac)
{
    //定義雅可比矩陣的大小，式65
    jac.create(total_num_matches_ * 3, num_images_ * 4, CV_64F);

    double val;
    const double step = 1e-3;    //表示步長，即式60中的∆

    for (int i = 0; i < num_images_; ++i)    //遍歷所有的匹配影象，即式65的所有行
    {
        for (int j = 0; j < 4; ++j)    //遍歷4個待精確的引數fu, rx, ry, rz
        {
            val = cam_params_.at<double>(i * 4 + j, 0);
            cam_params_.at<double>(i * 4 + j, 0) = val - step;
            calcError(err1_);
            cam_params_.at<double>(i * 4 + j, 0) = val + step;
            calcError(err2_);
            calcDeriv(err1_, err2_, 2 * step, jac.col(i * 4 + j));
            cam_params_.at<double>(i * 4 + j, 0) = val;
        }
    }
}

下面給出波形校正函式：

void waveCorrect(vector<Mat> &rmats, WaveCorrectKind kind)
//rmats表示所有相機的旋轉矩陣
//kind表示波形校正的方式，是水平校正（WAVE_CORRECT_HORIZ）還是垂直校正（WAVE_CORRECT_VERT）
{
    LOGLN("Wave correcting...");
#if ENABLE_LOG
    int64 t = getTickCount();    //用於計時
#endif
    //在前面已經分析過，程式中的旋轉矩陣其實是公式中旋轉矩陣的逆
    Mat moment = Mat::zeros(3, 3, CV_32F);    //表示矩量矩陣
    for (size_t i = 0; i < rmats.size(); ++i)    //遍歷所有的R，得到矩量矩陣
    {
        Mat col = rmats[i].col(0);    //提取旋轉矩陣的第一列
        moment += col * col.t();    //得到式67的方括號內的部分
    }
    Mat eigen_vals, eigen_vecs;    //表示特徵值和特徵向量
    eigen(moment, eigen_vals, eigen_vecs);    //計算矩量矩陣的特徵向量

    Mat rg1;    //表示校正矩陣的第二列，即式67的q1
    if (kind == WAVE_CORRECT_HORIZ)    //水平校正
        rg1 = eigen_vecs.row(2).t();    //最小特徵值對應的特徵向量
    else if (kind == WAVE_CORRECT_VERT)    //垂直校正
        rg1 = eigen_vecs.row(0).t();    //最大特徵值對應的特徵向量
    else    //其他情況
        CV_Error(CV_StsBadArg, "unsupported kind of wave correction");

    Mat img_k = Mat::zeros(3, 1, CV_32F);
    for (size_t i = 0; i < rmats.size(); ++i)
        img_k += rmats[i].col(2);    //計算∑r2
    Mat rg0 = rg1.cross(img_k);    //得到校正矩陣的第一列
    rg0 /= norm(rg0);    //歸一化處理，式68

    Mat rg2 = rg0.cross(rg1);    //得到校正矩陣的第三列，式69

    double conf = 0;    //表示置信度
    //根據置信度，調整校正矩陣的第一列和第二列
    if (kind == WAVE_CORRECT_HORIZ)    //水平校正
    {
        for (size_t i = 0; i < rmats.size(); ++i)
            conf += rg0.dot(rmats[i].col(0));
        if (conf < 0)
        {
            rg0 *= -1;
            rg1 *= -1;
        }
    }
    else if (kind == WAVE_CORRECT_VERT)    //垂直校正
    {
        for (size_t i = 0; i < rmats.size(); ++i)
            conf -= rg1.dot(rmats[i].col(0));
        if (conf < 0)
        {
            rg0 *= -1;
            rg1 *= -1;
        }
    }

    Mat R = Mat::zeros(3, 3, CV_32F);    //表示校正矩陣
    //構造校正矩陣
    Mat tmp = R.row(0);
    Mat(rg0.t()).copyTo(tmp);
    tmp = R.row(1);
    Mat(rg1.t()).copyTo(tmp);
    tmp = R.row(2);
    Mat(rg2.t()).copyTo(tmp);

    for (size_t i = 0; i < rmats.size(); ++i)    //遍歷所有的R
        rmats[i] = R * rmats[i];    //波形校正

    LOGLN("Wave correcting, time: " << ((getTickCount() - t) / getTickFrequency()) << " sec");
}

在影象拼接時，有時會出現輸入的影象不屬於全景影象的時候，因此我們還需要應用leaveBiggestComponent函式把這些影象剔除掉，只保留全景影象集合。應用並查集可以很方便的得到全景影象集合，而影象間能否拼接，依據的是匹配置信度c值的大小：

vector<int> leaveBiggestComponent(vector<ImageFeatures> &features,  vector<MatchesInfo> &pairwise_matches,
                                      float conf_threshold)
//features表示影象特徵
//pairwise_matches表示匹配點對的資訊
//conf_threshold表示匹配置信度c，即式23
//返回能夠拼接在一起的全景影象集合的索引
{
    const int num_images = static_cast<int>(features.size());    //得到待拼接影象的數量

    DisjointSets comps(num_images);    //例項化DisjointSets類，表示定義一個並查集
    //遍歷待拼接影象對，得到能夠拼接在一起的所有影象
    for (int i = 0; i < num_images; ++i) 
    {
        for (int j = 0; j < num_images; ++j)
        {
            //如果匹配置信度過小，則繼續下一次迴圈，即影象i和影象j無法拼接
            if (pairwise_matches[i*num_images + j].confidence < conf_threshold)
                continue;
            int comp1 = comps.findSetByElem(i);    //提取出第i幅影象的所在集合
            int comp2 = comps.findSetByElem(j);    //提取出第j幅影象的所在集合
            if (comp1 != comp2)    //表示影象i和影象j不屬於同一集合
                comps.mergeSets(comp1, comp2);    //合併兩個集合
        }
    }
    //得到元素最多的那個集合，即全景影象集合，max_comp表示該集合內元素（即影象）的數量
    int max_comp = static_cast<int>(max_element(comps.size.begin(), comps.size.end()) - comps.size.begin());
    //表示我們所需要的全景影象集合的元素索引，即max_comp所表示的那個集合
    vector<int> indices; 
    vector<int> indices_removed;    //表示不是全景影象集合的元素索引
    for (int i = 0; i < num_images; ++i)    //遍歷所有影象
        if (comps.findSetByElem(i) == max_comp)    //得到全景影象集合
            indices.push_back(i);    //得到影象索引
        else
            indices_removed.push_back(i);    //不是全景影象集合的元素索引

    vector<ImageFeatures> features_subset;    //表示特徵子集
    vector<MatchesInfo> pairwise_matches_subset;    //表示匹配子集
    //遍歷全景影象集合，得到特徵子集和匹配子集
    for (size_t i = 0; i < indices.size(); ++i)
    {
        features_subset.push_back(features[indices[i]]);    //得到特徵子集
        for (size_t j = 0; j < indices.size(); ++j)    //得到匹配子集
        {
            pairwise_matches_subset.push_back(pairwise_matches[indices[i]*num_images + indices[j]]);
            pairwise_matches_subset.back().src_img_idx = static_cast<int>(i);
            pairwise_matches_subset.back().dst_img_idx = static_cast<int>(j);
        }
    }
    //如果子集包括了所有影象，則直接退出，無需再執行下去
    if (static_cast<int>(features_subset.size()) == num_images)
        return indices;    //返回索引值
    //終端輸出
    LOG("Removed some images, because can't match them or there are too similar images: (");
    LOG(indices_removed[0] + 1);
    for (size_t i = 1; i < indices_removed.size(); ++i)
        LOG(", " << indices_removed[i]+1);
    LOGLN(").");
    LOGLN("Try to decrease the match confidence threshold and/or check if you're stitching duplicates.");
    //特徵和匹配資訊重新賦值
    features = features_subset;
    pairwise_matches = pairwise_matches_subset;

    return indices;    //返回索引值
}

3.3 應用

下面給出相機引數評估部分的應用，得到的引數在終端內輸出：

#include "opencv2/core/core.hpp"
#include "highgui.h"
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/features2d/features2d.hpp"
#include "opencv2/nonfree/nonfree.hpp"
#include "opencv2/legacy/legacy.hpp"

#include "opencv2/stitching/detail/autocalib.hpp"
#include "opencv2/stitching/detail/blenders.hpp"
#include "opencv2/stitching/detail/camera.hpp"
#include "opencv2/stitching/detail/exposure_compensate.hpp"
#include "opencv2/stitching/detail/matchers.hpp"
#include "opencv2/stitching/detail/motion_estimators.hpp"
#include "opencv2/stitching/detail/seam_finders.hpp"
#include "opencv2/stitching/detail/util.hpp"
#include "opencv2/stitching/detail/warpers.hpp"
#include "opencv2/stitching/warpers.hpp"

#include <iostream>
#include <fstream> 
#include <string>
#include <iomanip> 
using namespace cv;
using namespace std;
using namespace detail;

int main(int argc, char** argv)
{
   
   vector<Mat> imgs;    //得到待拼接影象佇列	
   Mat img = imread("1.jpg");
   imgs.push_back(img);
   img = imread("2.jpg");
   imgs.push_back(img);

   Ptr<FeaturesFinder> finder;    //特徵檢測
   finder = new SurfFeaturesFinder();
   vector<ImageFeatures> features(2);
    (*finder)(imgs[0], features[0]);
    (*finder)(imgs[1], features[1]);

   vector<MatchesInfo> pairwise_matches;    //特徵匹配
   BestOf2NearestMatcher matcher(false, 0.3f, 6, 6);
   matcher(features, pairwise_matches);

   HomographyBasedEstimator estimator;    //定義引數評估器
   vector<CameraParams> cameras;    //表示相機引數向量佇列
   estimator(features, pairwise_matches, cameras);    //相機引數評估

   cout<<"相機引數的初次評估："<<endl;    //終端輸出
   for (size_t i = 0; i < cameras.size(); ++i)
   {
      Mat R;
      cameras[i].R.convertTo(R, CV_32F);    //資料型別轉換
      cameras[i].R = R;
      cout<<"第"<<i+1<<"個相機的內參數"<< ":\n" << cameras[i].K()<<endl;
      cout<<"第"<<i+1<<"個相機的旋轉引數"<< ":\n" << R<<endl;
      cout<<"第