Introduction

神經網路功能強大。但是，其巨大的儲存和計算代價也使得其實用性特別是在移動裝置上的應用受到了很大限制。

所以，本文的目標就是：降低大型神經網路其儲存和計算消耗，使得其可以在移動裝置上得以執行，即要實現 “深度壓縮”。

實現的過程主要有三步：

（1） 通過移除不重要的連線來對網路進行剪枝；

（2） 對權重進行量化，使得許多連線共享同一權重，並且只需要儲存碼本(有效的權重)和索引；

（3） 進行霍夫曼編碼以利用有效權重的有偏分佈；

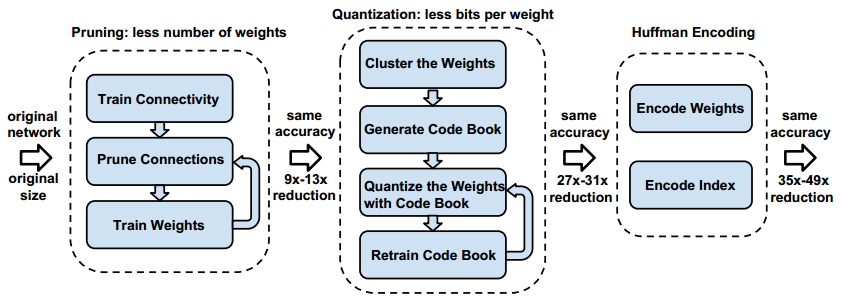
具體如下圖： 

Network Pruning

“剪枝”詳細點說也可以分為3步：

（1） 進行正常的網路訓練；

（2） 刪除所有權重小於一定閾值的連線

（3） 對上面得到的稀疏連線網路再訓練；

儲存稀疏結構時採用的是稀疏壓縮行CSR或者稀疏壓縮列CSC，假設非0元素個數為a,行或者列數為n,那麼我們需要儲存的資料量為 2a+n+1。 
以CSR為例，我們儲存時採用的是3元組結構，即：行優先儲存a個非零數，記為A；a個非零數所在列的列號；每一行第一個元素在A中的位置+非零數個數。

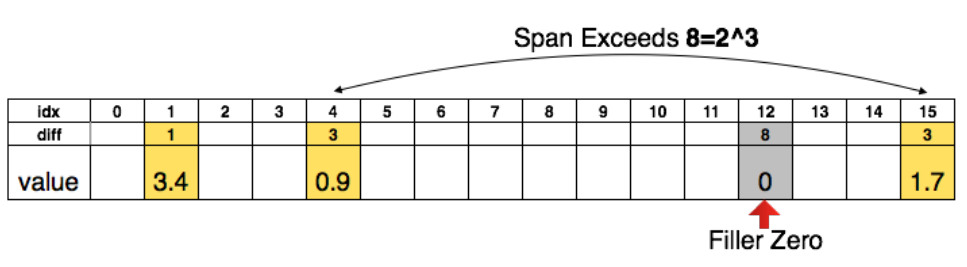
為了進一步壓縮，這裡不儲存絕對位置的索引，而是儲存相對位置索引。如果相對索引超過了8，那麼我們就人為補0。如下圖： 

Trained Quantization And Weight Sharing

這一部分通過對權重進行量化來進一步壓縮網路（量化可以降低表示資料所用的位數）。

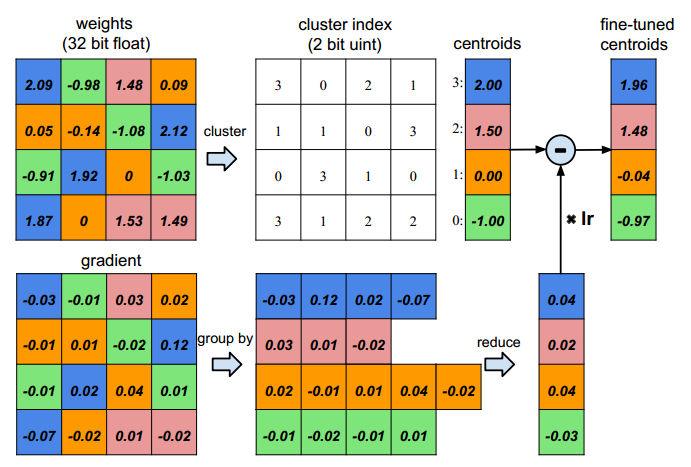
通過下圖，我們來說明如何對權重進行量化，以及後續又如何對量化網路進行再訓練。

首先，假設我們輸入神經元有4個，輸出神經元也是4個，那麼我們的weight應該是4x4，同樣梯度也是。

然後，我們量化權重為4階，即上圖用4種不同顏色表示。這樣的話我們就只需要儲存4個碼字以及16個2bit的索引。

最後，我們應該如何再訓練，即如何對量化值進行更新。事實上，我們僅對碼字進行更新。具體如上圖的下部分：計算相同索引處的梯度之和，然後乘以學習率，對相應的碼字進行更新。

實際當中，對於AlexNet,作者對卷積層使用了8bit量化(即有256個碼字)，對全連線層使用了5bit量化(即有32個碼字)，但是卻不損失效能

關於如何確定碼字：

作者對訓練好網路的每一層（即不同層之間權重不共享）的權重進行K-means，聚類中心便是要求的碼字。有一點需要注意，K-means聚類時需要初始化聚類中心，不同的初始化方法對最後的聚類結果影響很大，從而也會影響網路的預測精度。這裡比較了Forgy(random), density-based, and linear initialization這三種初始化方法。

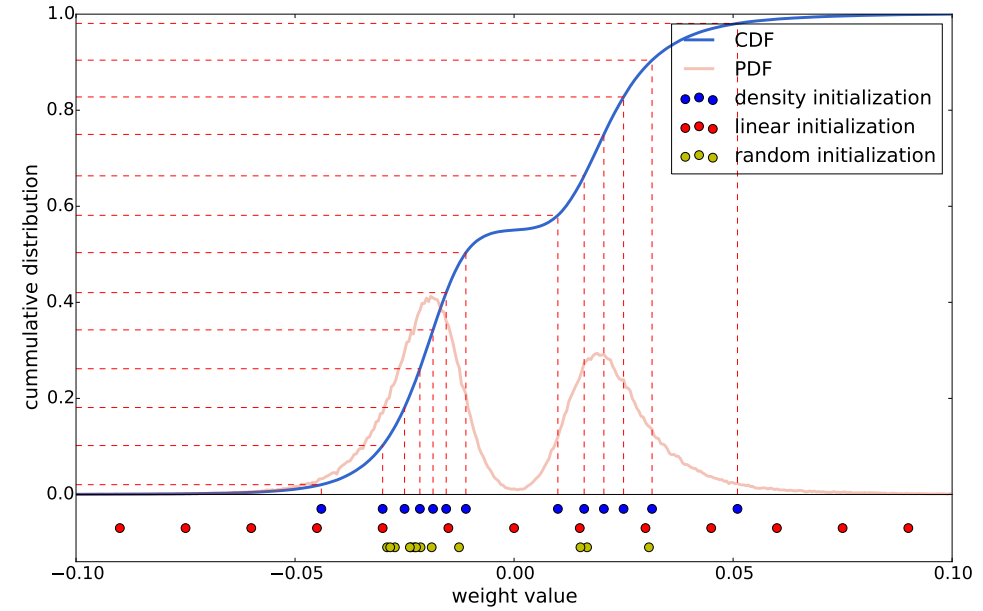
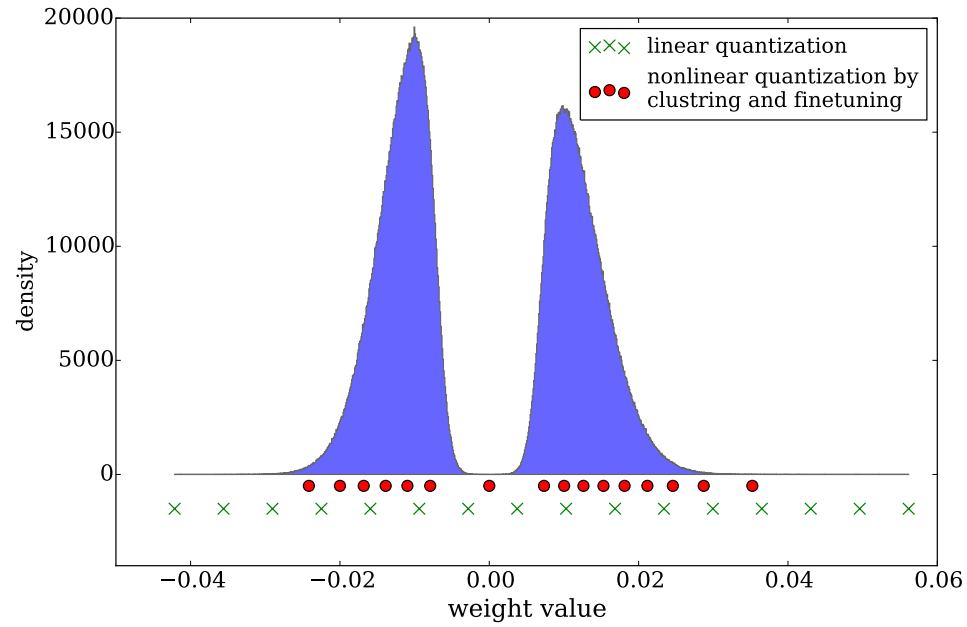
下圖畫出了AlexNet中conv3層的權重分佈，其中紅色線表示概率密度分佈PDF，藍色線表示CDF。顯然，剪枝後的網路權重符合雙峰分佈。圖的下方，顯示了3種不同初始化方法最後收斂到的聚類中心。

有一點我們需要注意：大權重比小權重的作用要大。因此，從上圖來看雖然Forgy(random), density-based方法比較好的擬合了資料分佈，但是它們忽略了那些絕對值較大的權重，而linear initialization就不會有這個問題。

因此，文章採用線性初始化，實驗也證明了其正確性。

下圖是finetune前後的碼字分佈： 

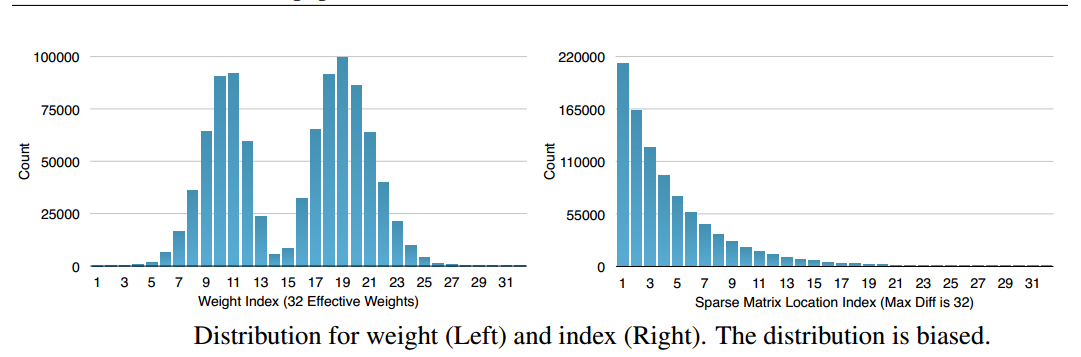
Huffman Coding

Huffman編碼按照符號出現的概率來進行變長編碼。下面的權重以及索引分佈來自於AlexNet的最後一個全連線層。由圖可以看出，其分佈是非均勻的，因此我們可以利用Huffman編碼來對其進行處理，最終可以使的網路的儲存減少20%~30%。 

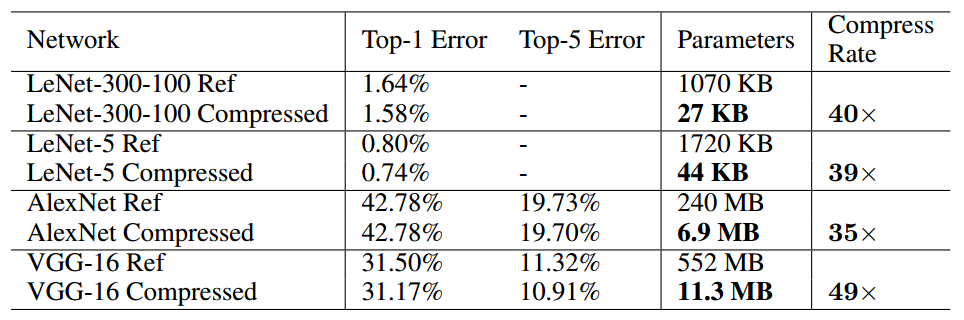
Experiment Results

文章主要在LeNet、AlexNet和VGGNet上做的實驗，我這裡只列出一部分。