目標追蹤演算法KCF(kernelized correlation filters)論文學習筆記
最近一直在研究KCF演算法,看了原論文和很多相關部落格,本篇博文原作者:http://www.cnblogs.com/YiXiaoZhou/p/5925019.html。我增加了一些自己的理解與思考。
讀"J. F. Henriques, R. Caseiro, P. Martins, J. Batista, 'High-speed tracking with kernelized correlation filters'" 筆記
KCF是一種鑑別式追蹤方法,這類方法一般都是在追蹤過程中訓練一個目標檢測器,使用目標檢測器去檢測下一幀預測位置是否是目標,然後再使用新檢測結果去更新訓練集進而更新目標檢測器。而在訓練目標檢測器時一般選取目標區域為正樣本,目標的周圍區域為負樣本,當然越靠近目標的區域為正樣本的可能性越大。
注意論文中關於向量是行向量還是列向量總是指示不清楚,所以本文對變數符號統一之後進行推導,首先所有的小寫字母均表示列向量,所有的大寫字母表示矩陣,其中矩陣的每一行是一個樣本,文中的函式除了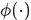 是對行向量操作,其餘都是對元素操做的,四則運算子號也都是針對元素操作的。還有所有對迴圈矩陣使用傅立葉變換時使用的生成向量都是迴圈矩陣的第一行向量,這點很重要。
是對行向量操作,其餘都是對元素操做的,四則運算子號也都是針對元素操作的。還有所有對迴圈矩陣使用傅立葉變換時使用的生成向量都是迴圈矩陣的第一行向量,這點很重要。
KCF的主要貢獻
-
使用目標周圍區域的迴圈矩陣採集正負樣本,利用脊迴歸訓練目標檢測器,併成功的利用迴圈矩陣在傅立葉空間可對角化的性質將矩陣的運算轉化為向量的Hadamad積,即元素的點乘,大大降低了運算量,提高了運算速度,使演算法滿足實時性要求。
-
將線性空間的脊迴歸通過核函式對映到非線性空間,在非線性空間通過求解一個對偶問題和某些常見的約束,同樣的可以使用迴圈矩陣傅立葉空間對角化簡化計算。
-
給出了一種將多通道資料融入該演算法的途徑。
一維脊迴歸
脊迴歸
設訓練樣本集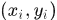 ,那麼其線性迴歸函式
,那麼其線性迴歸函式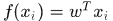 ,
,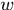 是列向量表示權重係數,可通過最小二乘法求解
是列向量表示權重係數,可通過最小二乘法求解
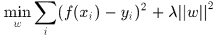
其中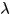 用於控制系統的結構複雜性,也就是VC維以保證分類器的泛化效能。
用於控制系統的結構複雜性,也就是VC維以保證分類器的泛化效能。
寫成矩陣形式
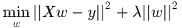
其中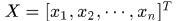 的每一行表示一個向量,
的每一行表示一個向量,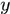 是列向量,每個元素對應一個樣本的標籤,於是令導數為0,可求得
是列向量,每個元素對應一個樣本的標籤,於是令導數為0,可求得
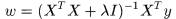
因為後面實在傅立葉域內計算,牽涉到複數矩陣,所以我們將結果都統一寫成複數域中形式

其中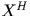 表示複共軛轉置矩陣。
表示複共軛轉置矩陣。
迴圈矩陣
KCF中所有的訓練樣本是由目標樣本迴圈位移得到的,向量的迴圈可有排列矩陣得到,比如
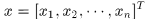


當然對於二維影象的話,可以通過x軸和y軸分別迴圈移動實現不同位置的移動

舉例

1474942884758.jpg

1474942898329.jpg
所以由一個向量 可以通過不斷的乘上排列矩陣得到n個迴圈移位向量,將這n個向量依序排列到一個矩陣中,就形成了x生成的迴圈矩陣,表示成
可以通過不斷的乘上排列矩陣得到n個迴圈移位向量,將這n個向量依序排列到一個矩陣中,就形成了x生成的迴圈矩陣,表示成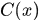
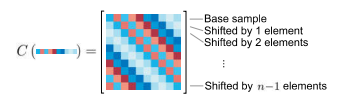
1D向量得到的迴圈矩陣.jpg

2D影象不同迴圈次數後的移位.jpg
迴圈矩陣傅氏空間對角化
所有的迴圈矩陣都能夠在傅氏空間中使用離散傅立葉矩陣進行對角化
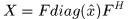
其中x對應於生成X的向量(就是X的第一行矩陣)的傅立葉變化後的值, ,
,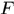 是離散傅立葉矩陣,是常量
是離散傅立葉矩陣,是常量
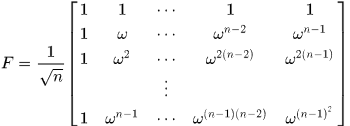
關於矩陣的傅立葉對角化請參加 迴圈矩陣傅立葉對角化,後面的筆記會專門講解傅立葉變換。
傅氏對角化簡化的脊迴歸
將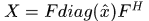 帶入脊迴歸公式得到
帶入脊迴歸公式得到
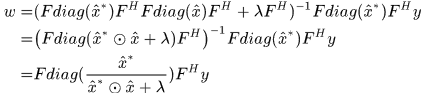
注意這裡的分號是點除運算,就是對應元素相除。因為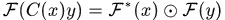 ,(
迴圈矩陣傅立葉對角化)對上式兩邊同時傅氏變換得
,(
迴圈矩陣傅立葉對角化)對上式兩邊同時傅氏變換得
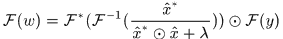
於是
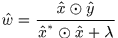
這裡和論文式(12)不一樣,論文裡(12)式分子上似乎多了個共軛符號,因為Appendix A.5中的式(55)後面那個 應該是少了個共軛轉置符號。
應該是少了個共軛轉置符號。
這樣就可以使用向量的點積運算取代矩陣運算,特別是求逆運算,大大提高了計算速度。

核空間的脊迴歸
我們希望找到一個非線性對映函式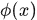 列向量,使對映後的樣本在新空間中線性可分,那麼在新空間中就可以使用脊迴歸來尋找一個分類器
列向量,使對映後的樣本在新空間中線性可分,那麼在新空間中就可以使用脊迴歸來尋找一個分類器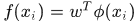 ,所以這時候得到的權重係數為
,所以這時候得到的權重係數為

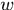 是
是 行向量張成的空間中的一個向量,所以可以令
行向量張成的空間中的一個向量,所以可以令
上式就變為
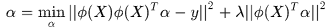
該問題稱為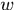 的對偶問題
的對偶問題
令關於列向量 導數為0,
導數為0,
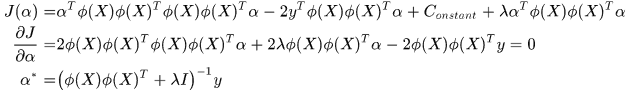
注: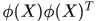 其實類似於核空間變數的協方差矩陣,矩陣的轉置乘以矩陣,一定可逆。
其實類似於核空間變數的協方差矩陣,矩陣的轉置乘以矩陣,一定可逆。
對於核方法,我們一般不知道非線性對映函式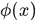 的具體形式,而只是刻畫在核空間的核矩陣
的具體形式,而只是刻畫在核空間的核矩陣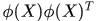 ,那麼我們令
,那麼我們令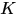 表示核空間的核矩陣,由核函式得到,那麼
表示核空間的核矩陣,由核函式得到,那麼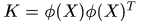
於是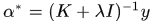
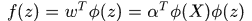
論文提出的一個創新點就是使迴圈矩陣的傅氏對角化簡化計算,所以這裡如果希望計算 時可以同樣將矩陣求逆運算變為元素運算,就希望將
時可以同樣將矩陣求逆運算變為元素運算,就希望將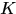 對角化,所以希望找到一個核函式使對應的核矩陣式迴圈矩陣。
對角化,所以希望找到一個核函式使對應的核矩陣式迴圈矩陣。
Theorem 1. Given circulant data C(x), the corresponding kernel matrix K is circulatant if the kernel function satisfies
,for any permutation matrix M.
即核矩陣是迴圈矩陣應該滿足兩個條件:第一個樣本和第二個樣本都是由生成樣本迴圈移位產生的,可以不是由同一個樣本生成;滿足,其中
是排列矩陣。
證明:設 ,則
,則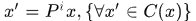 ,於是
,於是

因為K的第一行為 所以
所以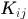 相當於將第一行的第
相當於將第一行的第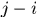 個元素放到K的第i行j列上,
個元素放到K的第i行j列上,
那麼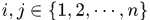 就得到了迴圈矩陣,所以
就得到了迴圈矩陣,所以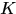 是迴圈矩陣。證明裡
是迴圈矩陣。證明裡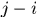 表示除
表示除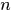 的餘數,因為這個過程是迴圈的。
的餘數,因為這個過程是迴圈的。
證畢。
若K是迴圈矩陣,則
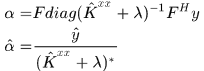
其中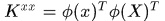 是K中第一行。這裡覺得奇怪?兩個轉置?這是因為我們已經約定
是K中第一行。這裡覺得奇怪?兩個轉置?這是因為我們已經約定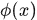 是列向量,而
是列向量,而 的第i行是
的第i行是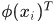 ,是不是明白了~
,是不是明白了~
這裡推出來的公式和論文中公式(17)也不大一樣
那麼那些核函式滿足上述性質呢?論文中給出
-
Radial Basis Function kernels -e.g. Gaussian
-
Dot-Product kernels -e.g. linear, polynomial
-
Additive kernels - e.g. intersection,
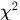 and Hellinger kernels
and Hellinger kernels -
Exponentiated additive kernels.
快速檢測
首先由訓練樣本和標籤訓練檢測器,其中訓練集是由目標區域和由其移位得到的若干樣本組成,對應的標籤是根據距離越近正樣本可能性越大的準則賦值的,然後可以得到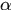
待分類樣本集,即待檢測樣本集,是由預測區域和由其移位得到的樣本集合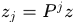
那麼就可以選擇 最大的樣本作為檢測出的新目標區域,由
最大的樣本作為檢測出的新目標區域,由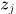 判斷目標移動的位置。
判斷目標移動的位置。
定義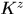 是測試樣本和訓練樣本間在核空間的核矩陣
是測試樣本和訓練樣本間在核空間的核矩陣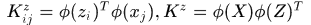
由於核矩陣滿足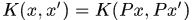 ,即
,即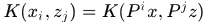 類似於theorem
1 的證明可得
類似於theorem
1 的證明可得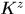 是迴圈矩陣
是迴圈矩陣
我記得曾經見到過有人問 非方陣的情況,假設取樣視窗非方形,即
非方陣的情況,假設取樣視窗非方形,即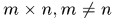 那麼取樣視窗通過移位都會產生
那麼取樣視窗通過移位都會產生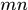 個樣本,無論是訓練樣本還是測試樣本,所以
個樣本,無論是訓練樣本還是測試樣本,所以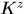 一定是方陣
一定是方陣
於是得到各個測試樣本的響應
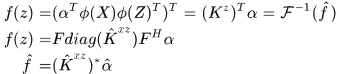
注意我們說過小寫的都是列向量,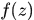 是列向量。注意我們這裡
是列向量。注意我們這裡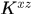 是矩陣
是矩陣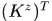 的第一行,即
的第一行,即 的第一列,而文中(22)式中
的第一列,而文中(22)式中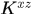 是論文中
是論文中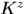 的第一行,這是因為本文和論文中關於
的第一行,這是因為本文和論文中關於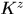 的定義正好是相轉置的。也就是說我覺得(22)式只是少了一個共軛。。。
的定義正好是相轉置的。也就是說我覺得(22)式只是少了一個共軛。。。
覺得蠻奇怪的,怎麼和論文中推導結果好多都差一個共軛符號??
這是因為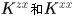 都是對稱向量,而對稱向量的共軛轉置是實數,所以就和論文中一樣了,這點參考KCF高速跟蹤詳解
都是對稱向量,而對稱向量的共軛轉置是實數,所以就和論文中一樣了,這點參考KCF高速跟蹤詳解
核矩陣的快速計算
現在還存在的矩陣運算就是核矩陣的第一行的計算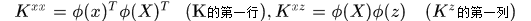
內積和多項式核
這種核函式核矩陣可以表示成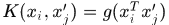 ,於是
,於是

因此對於多項式核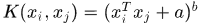 有
有
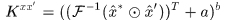
徑向基核函式
比如高斯核,這類函式是 的函式
的函式
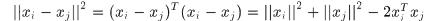
所以
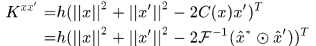
對於高斯核則有
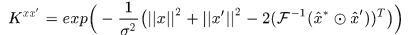
1D到2D
上面公式推導的很爽,可是都是在1D情況下得到了結論,2D影象該怎麼辦呢?
這個問題困擾了我好久。。。。剛開始我也想從線性空間的脊迴歸推導,假設 是目標影象,
是目標影象, 是由
是由 生成的迴圈矩陣塊,即
生成的迴圈矩陣塊,即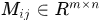 表示
表示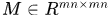 的第
的第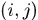 塊,是由
塊,是由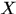 右移
右移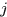 ,下移
,下移 得到的樣本塊。那麼即使塊迴圈矩陣能夠通過2D傅立葉變換矩陣對角化又怎麼用呢??因為我們不可能帶入
得到的樣本塊。那麼即使塊迴圈矩陣能夠通過2D傅立葉變換矩陣對角化又怎麼用呢??因為我們不可能帶入 類似的式子中啊(這個式子是類比於1D脊迴歸寫的,並無實際意義)
類似的式子中啊(這個式子是類比於1D脊迴歸寫的,並無實際意義)
哎呀,想破腦袋啊!
啊哈,想明白了,線性假設下沒辦法用,直接在核空間推導,發現豁然開朗~
現在有一個函式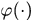 ,自變數
,自變數 ,因變數
,因變數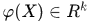 ,也不知道怎麼對映的,也不知道
,也不知道怎麼對映的,也不知道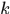 是多少,反正是個確定但未知的值。那麼在核空間我們就可以使用脊迴歸的公式了~
是多少,反正是個確定但未知的值。那麼在核空間我們就可以使用脊迴歸的公式了~

注意:由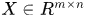 移位生成的樣本共有
移位生成的樣本共有 個,所以
個,所以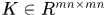 ,這裡
,這裡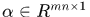 ,
,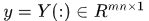 是對應樣本的標籤,
是對應樣本的標籤, 是對應樣本標籤的矩陣形式。
是對應樣本標籤的矩陣形式。
ok,現在再來看看定理2
Theorem 2. The block matrix
with elements
相關推薦
目標追蹤演算法KCF(kernelized correlation filters)論文學習筆記
最近一直在研究KCF演算法,看了原論文和很多相關部落格,本篇博文原作者:http://www.cnblogs.com/YiXiaoZhou/p/5925019.html。我增加了一些自己的理解與思考。 讀"J. F. Henriques, R. Caseir
《演算法導論(第3版)》讀書筆記(一)演算法基礎
本篇內容主要涉及《演算法導論》一書中的第二章知識,涉及的內容有插入排序和歸併排序 插入排序 對於插入排序有個很明顯的顯示生活例子來幫助我們理解,插入排序的工作原理就像打撲克牌一樣,右手從桌面上拿起一張牌,然後再左手那一堆已經按牌面大小排好序的牌找
《Qt5 開發與實例(第三版)》學習筆記(七)
clu idg center ble mil detached pre tab etc 1 // 3.2 停靠窗口 QDockWidget類 2 setFeatures() 3 setAllowedAreas() 4 setWidget() 5 addDockW
《Qt5 開發與實例(第三版)》學習筆記(九)
nal inf lin exc ken right item vbo ott 1 // 3.4 基本布局(QLayout) 2 //dialog.h 3 #ifndef DIALOG_H 4 #define DIALOG_H 5 6 #incl
《Qt5 開發與實例(第三版)》學習筆記(八)
nbsp font public insert enter body win parent hbox 1 // 3.3 堆棧窗體 QStackedWidget類 2 //stackdlg.h 3 #ifndef STACKDLG_H 4 #define STACK
《Qt5 開發與實例(第三版)》學習筆記(十)
fix row tac person als new .cpp exec constrain 1 // 3.5 『綜合實例』 修改用戶資料 2 //main.cpp 3 #include "content.h" 4 #include <QApplic
《Qt5 開發與實例(第三版)》學習筆記(五)
液晶 lag bool child gles 操作 啟動 ring home 1 //2.5 控件 2 //2.51 按鈕組(Buttons) 3 /* 4 Radio Button //單選按鈕 5 Check Box//復選框 6 Dialog
《Qt5 開發與實例(第三版)》學習筆記(四)
常用 斷言 max swap 正則表達 4.2 debug 實例 筆記 1 //2.4 算法及正則表達式 2 //2.4.1 Qt5常用算法 3 double c=qAbs(a);//返回絕對值 4 double max=qMax(b,c);//返回最大值 5
《Qt5 開發與實例(第三版)》學習筆記(十二)
action spa 添加 png esb geb itl msgbox setw 1 // 4.2 Qt5 自定義對話框 2 #include <QMessageBox> 3 4 void Dialog::showCustomMsgBox() 5
(print除去省略號)tensorflow學習筆記(北京大學) tf4_1_0.py 完全解析 列印完整資料
# -*- coding: utf-8 -*- """ Created on Thu Nov 1 12:24:34 2018 #tensorflow學習筆記(北京大學) tf3_7_0.py 完全解析 列印完整資料 #QQ群:476842922(歡迎加群討論學習 """ import te
GitHub超過4700星的TensorFlow(Amirsina Torfi博士)程式碼學習筆記(二)
上次的比較基礎,本章節(第二個檔案)主要是基礎機器學習模型學習。和筆記(一)相比較複雜,並且很多模型我都沒有引用成功。避免文章太長 ,所以本文只學習gradient_boosted_decision_tree.py,kmeans.py和linear_regression.py 完整程式碼連結
GitHub超過4700星的TensorFlow(Amirsina Torfi博士)程式碼學習筆記(一)
用TensorFlow的應該都知道,git上的一個大神弗吉尼亞理工博士Amirsina Torfi在GitHub上貢獻了一個新的教程,星星數當天就破千,現在已經4721了,估計這個文章寫完又得漲點。 完整程式碼連結(1積分):https://download.csdn.net/downloa
《組合語言(第3版)(王爽 著)》學習筆記一:基礎知識(1)
組合語言是直接在硬體之上工作的程式語言,我們首先要了解硬體系統的結構,才能有效地應用匯編語言對其程式設計。 彙編課程的研究重點放在如何利用硬體系統的程式設計結構和指令集有效靈活地控制系統進行工作。
《組合語言(第3版)(王爽 著)》學習筆記二:基礎知識(2)
1.7 CPU 對儲存器的讀寫 以上講到,儲存器被劃分成多個儲存單元,儲存單元從零開始編號。這些編號可以看作儲存單元在儲存器中的地址。就想一條街,每個房子都有門牌號碼。 CPU 要從記憶體中讀資料,
《組合語言(第3版)(王爽 著)》學習筆記三:基礎知識(3)
1.11 記憶體地址空間(概述) 什麼是記憶體地址空間呢?舉例來講,一個 CPU 的地址匯流排寬度為 10,那麼可以定址 1024 個記憶體單元,這 1024 個可尋到的記憶體單元就構成這個 CPU
《C#入門經典(第6版)》學習筆記_第10章_定義類成員
第10章 定義類成員 本章內容: 如何定義類成員 如何使用類圖新增成員 如何控制類成員的繼承 如何定義巢狀的類 如何實現介面 如何使用部分類定義 如何使用Call Hierarchy視窗 10.1 成員定義 在類定義中,也提供了該類中
《C#入門經典(第6版)》學習筆記_第6章_函式
第103頁-第128頁,共26頁。 本章內容: 如何定義和使用不接受任何資料也不返回任何資料的簡單函式 如何在函式中傳入傳出資料 使用變數作用域 如何結合使用Main()函式和命令列引數 如何把函式提供為結構型別的成員 如何使用函式過載 如何使用委託 本章介
《C程式設計(第四版)》學習筆記
參考教材:譚浩強的《C程式設計(第四版)》 序——對好書的定義:(20130106) 1、定位準確。要明確讀者物件,要有的放矢,不要不問物件,提筆就寫。 2、內容先進。要能反映計算機科學技術的新成果、新趨勢。 3、取捨合理。要做到“該有的有,不該有的沒有”,不要包羅
【《計算機網路(第七版)》學習筆記】三、 資料鏈路層
3.1 使用點對點的通道的資料鏈路層 點對點通道:一對一 廣播通道 : 一對多 3.1.1 資料鏈路和幀 鏈路:是一條無源的點到點的物理線路段,中間沒有任何其他的交換節點 資料鏈路:除了物理線路外,還必須有通訊協議來控制這些資料的傳輸。若把實現
《TensorFlow實戰Google深度學習框架(2017.3第一版)》學習筆記(一)
書本3.1.2計算圖的使用中的第41頁,例項中 v = tf.get_variable( 'v', initializer = tf.zeros_initializer(shape = [1])) 報錯 原因在於新版的tensorflow將語法改為 v
