1. 線性表？分類（優缺點，查詢、刪除、插入的複雜度）？例子？
2. 連結串列和線性表的關係？
3. 連結串列的分類？是根據什麼劃分的？

線性表

線性表中資料元素之間的關係是一對一的關係，即除了第一個和最後一個數據元素之外，其它資料元素都是首尾相接的。

線性表分類：順序儲存結構、鏈式儲存結構

例子：陣列

順序儲存結構：兩個相鄰的元素在記憶體中也是相鄰的。通過首地址和偏移量就可以直接訪問到某元素，關於查詢的適配演算法很多，最快可以達到O(logn)。缺點是插入和刪除的時間複雜度最壞能達到O(n)，要開闢稍大點的記憶體，造成記憶體浪費。

鏈式儲存結構：相鄰的元素在記憶體中可能不是相鄰的，每一個元素都有一個指標域，指標域一般是儲存著到下一個元素的指標。優點是插入和刪除的時間複雜度為O(1)，不會浪費太多記憶體，新增元素的時候才會申請記憶體，刪除元素會釋放記憶體，。缺點是訪問的時間複雜度最壞為O(n)，關於查詢的演算法很少，一般只能遍歷，這樣時間複雜度也是線性（O(n)）的了,頻繁的申請和釋放記憶體也會消耗時間。

連結串列

 連結串列就是鏈式儲存的線性表。

根據指標域的不同，連結串列分為單向連結串列、雙向連結串列、迴圈連結串列等等。

單向連結串列

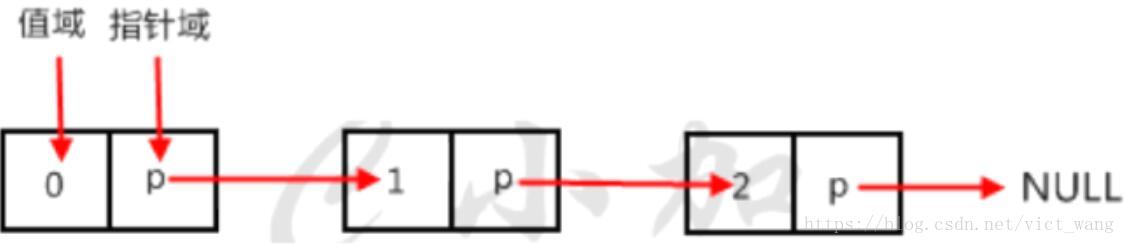
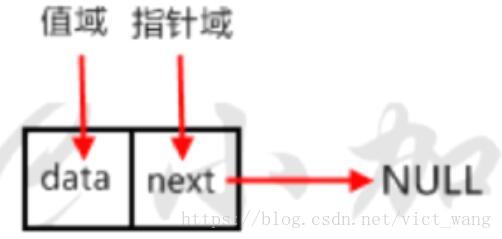
每個元素包含兩個域，值域和指標域，我們把這樣的元素稱之為節點。每個節點的指標域內有一個指標，指向下一個節點，而最後一個節點則指向一個空值（一個方向遍歷）。如圖就是一個單向連結串列。

程式碼編寫：

1.寫節點類，則連結串列中的每一個結點可表示出來（例項化）

template<class T>
class slistNode
{
    public:
    slistNode(){next=NULL;}//初始化
    T data;//值
    slistNode* next;//指向下一個節點的指標
};
 

2.寫單鏈表類的宣告，包括屬性和方法。

template<class T>
class myslist
{
    private:
        unsigned int listlength;
        slistNode<T>* node;//臨時節點
        slistNode<T>* lastnode;//尾結點
        slistNode<T>* headnode;//頭節點
    public:
        myslist();//初始化
        unsigned int length();//連結串列元素的個數
        void add(T x);//表尾新增元素
        void traversal();//遍歷整個連結串列並列印
        bool isEmpty();//判斷連結串列是否為空
        slistNode<T>* find(T x);//查詢第一個值為x的節點,返回節點的地址,找不到返回NULL
        void Delete(T x);//刪除第一個值為x的節點
        void insert(T x,slistNode<T>* p);//在p節點後插入值為x的節點
        void insertHead(T x);//在連結串列的頭部插入節點
};
 

 3.寫建構函式，初始化連結串列類的屬性。

template<class T>
myslist<T>::myslist()
{
    node=NULL;
    lastnode=NULL;
    headnode=NULL;
    listlength=0;
}

4.方法的實現

template<class T>
void  myslist<T>::add(T x)
{
    node=new slistNode<T>();//申請一個新的節點
    node->data=x;//新節點賦值為x
    if(lastnode==NULL)//如果沒有尾節點則連結串列為空,node既為頭結點,又是尾節點
    {
        headnode=node;
        lastnode=node;
    }
    else//如果連結串列非空
    {
        lastnode->next=node;//node既為尾節點的下一個節點
        lastnode=node;//node變成了尾節點,把尾節點賦值為node
    }
    ++listlength;//元素個數+1
}

template<class T>
void  myslist<T>::traversal()
{
    node=headnode;//用臨時節點指向頭結點
    while(node!=NULL)//遍歷連結串列並輸出
    {
        cout<<node->data<<ends;
        node=node->next;
    }
    cout<<endl;
}

template<class T>
bool  myslist<T>::isEmpty()
{
    return listlength==0;
}

template<class T>
slistNode<T>* myslist<T>::find(T x)
{
    node=headnode;//用臨時節點指向頭結點
    while(node!=NULL&&node->data!=x)//遍歷連結串列,遇到值相同的節點跳出
    {
        node=node->next;
    }
    return node;//返回找到的節點的地址,如果沒有找到則返回NULL
}

 5.刪除插入方法的解析，刪除第一個值為x的節點，如圖

template<class T>
void  myslist<T>::Delete(T x)
{
    slistNode<T>* temp=headnode;//申請一個臨時節點指向頭節點
    if(temp==NULL) return;//如果頭節點為空,則該連結串列無元素,直接返回
    if(temp->data==x)//如果頭節點的值為要刪除的值,則刪除投節點
    {
        headnode=temp->next;//把頭節點指向頭節點的下一個節點
        if(temp->next==NULL) lastnode=NULL;//如果連結串列中只有一個節點,刪除之後就沒有節點了,把尾節點置為空
        delete(temp);//刪除頭節點
        return;
    }
    while(temp->next!=NULL&&temp->next->data!=x)//遍歷連結串列找到第一個值與x相等的節點,temp表示這個節點的上一個節點
    {
        temp=temp->next;
    }
    if(temp->next==NULL) return;//如果沒有找到則返回
    if(temp->next==lastnode)//如果找到的時候尾節點
    {
        lastnode=temp;//把尾節點指向他的上一個節點
        delete(temp->next);//刪除尾節點
        temp->next=NULL;
    }
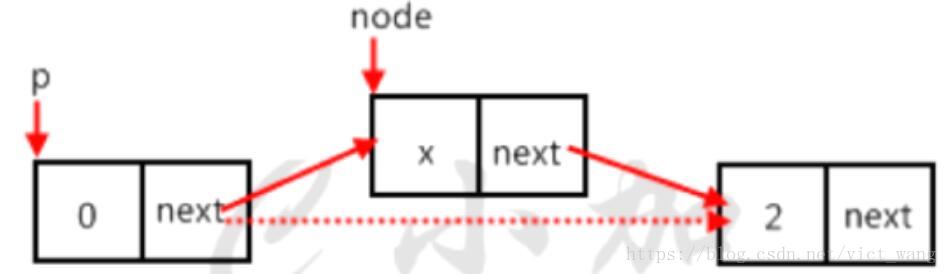
    else//如果不是尾節點,如圖4
    {
        node=temp->next;//用臨時節點node指向要刪除的節點
        temp->next=node->next;//要刪除的節點的上一個節點指向要刪除節點的下一個節點
        delete(node);//刪除節點
        node=NULL;
    }
}

6.實現insert()和insertHead()函式，在p節點後插入值為x的節點。如圖

template<class T>
void  myslist<T>::insert(T x,slistNode<T>* p)
{
    if(p==NULL) return;
    node=new slistNode<T>();//申請一個新的空間
    node->data=x;//如圖5
    node->next=p->next;
    p->next=node;
    if(node->next==NULL)//如果node為尾節點
    lastnode=node;
}
template<class T>
void  myslist<T>::insertHead(T x)
{
    node=new slistNode<T>();
    node->data=x;
    node->next=headnode;
    headnode=node;
}

 雙向連結串列

雙向連結串列的指標域有兩個指標，每個資料結點分別指向直接後繼和直接前驅。單向連結串列只能從表頭開始向後遍歷，而雙向連結串列不但可以從前向後遍歷，也可以從後向前遍歷。除了雙向遍歷的優點，雙向連結串列的刪除的時間複雜度會降為O（1），因為直接通過目的指標就可以找到前驅節點，單向連結串列得從表頭開始遍歷尋找前驅節點。缺點是每個節點多了一個指標的空間開銷。如圖就是一個雙向連結串列。

迴圈連結串列

 迴圈連結串列就是讓連結串列的最後一個節點指向第一個節點，這樣就形成了一個圓環，可以迴圈遍歷。單向迴圈連結串列可以單向迴圈遍歷，雙向迴圈連結串列的頭節點的指標也要指向最後一個節點，這樣的可以雙向迴圈遍歷。如圖就是一個雙向迴圈連結串列。

  連結串列相關面試問題

1. 如何判斷一個單鏈表有環
2. 如何判斷一個環的入口點在哪裡
3. 如何知道環的長度
4. 如何知道兩個單鏈表（無環）是否相交
5. 如果兩個單鏈表（無環）相交，如何知道它們相交的第一個節點是什麼
6. 如何知道兩個單鏈表（有環）是否相交
7. 如果兩個單鏈表（有環）相交，如何知道它們相交的第一個節點是什麼

#include <iostream>
#define ListNodePosi(T) ListNode<T>*//指標指向列表的結點:裡面含有兩個指標pred和succ
typedef int Rank;

template <typename T>
class ListNode//列表節點模板類（以雙向連結串列形式實現）
{
public:
	T data;
	ListNode<T>* pred;//節點的前驅指標:指向前結點，而不是前節點的前驅或後驅指標
	ListNode<T>* succ;//節點的後繼指標:指向後結點，而不是後節點的前驅或後驅指標
	//建構函式
	ListNode(){}
	ListNode(T e, ListNodePosi(T) p = NULL, ListNodePosi(T) s = NULL) :data(e), pred(p), succ(s)
	{
		//預設構造器
	}
	//操作介面
	ListNode<T>* insertAsPred(T const& e);//結點前插入
	ListNode<T>* insertAsSucc(T const& e);//結點後插入
};
//note:連結串列節點類主要用於構建列表，所以直接用public

#include "listNode.h"
template <typename T>
class List
{
private://私有的頭哨兵和尾哨兵對外部不可見（eg:valid中從外部被等效的視為NULL）,首節點尾結點是頭哨兵之後的，尾哨兵之前的
	int _size;
	ListNode<T>* header;//頭哨兵:header->succ代表頭結點
	ListNode<T>* trailer;//尾哨兵
protected:
	void init();
	int clear();
	void copyNodes(ListNodePosi(T) p, int n);
	void merge(ListNodePosi(T)&, int, List<T>&, ListNodePosi(T), int);//有序列表區間合併
	void merge(List<T>& L) { merge(first(), size, L, L.first(), _size); }//全列表合併
	void mergeSort(ListNodePosi(T)& p, int n);//對從p開始的n個節點歸併排序
	void selectionSort(ListNodePosi(T) p, int n);//...選擇排序
	void insertionSort(ListNodePosi(T) p, int n);//插入排序
public:
	List() { init(); }
	List(List<T> const& L);
	List(List<T> const& L, Rank r, int n);
	List(ListNodePosi(T) p, int n);
	~List();//釋放所有節點
..............
}