神經網路基礎

1、神經元（Neuron）——就像形成我們大腦基本元素的神經元一樣，神經元形成神經網路的基本結構。想象一下，當我們得到新資訊時我們該怎麼做。當我們獲取資訊時，我們一般會處理它，然後生成一個輸出。類似地，在神經網路的情況下，神經元接收輸入，處理它併產生輸出，而這個輸出被髮送到其他神經元用於進一步處理，或者作為最終輸出進行輸出。

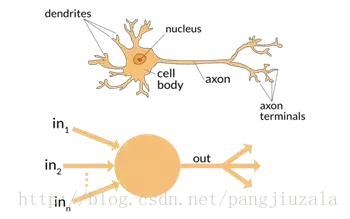
2、權重（Weights）——當輸入進入神經元時，它會乘以一個權重。例如，如果一個神經元有兩個輸入，則每個輸入將具有分配給它的一個關聯權重。我們隨機初始化權重，並在模型訓練過程中更新這些權重。訓練後的神經網路對其輸入賦予較高的權重，這是它認為與不那麼重要的輸入相比更為重要的輸入。為零的權重則表示特定的特徵是微不足道的。

讓我們假設輸入為 a，並且與其相關聯的權重為 W1，那麼在通過節點之後，輸入變為 a *W1。

3、偏差（Bias）——除了權重之外，另一個被應用於輸入的線性分量被稱為偏差。它被加到權重與輸入相乘的結果中。基本上新增偏差的目的是來改變權重與輸入相乘所得結果的範圍的。新增偏差後，結果將看起來像 a* W1 偏差。這是輸入變換的最終線性分量。

4、啟用函式（Activation Function）——一旦將線性分量應用於輸入，將會需要應用一個非線性函式。這通過將啟用函式應用於線性組合來完成。啟用函式將輸入訊號轉換為輸出訊號。應用啟用函式後的輸出看起來像 f（a *W1+ b），其中 f（）就是啟用函式。

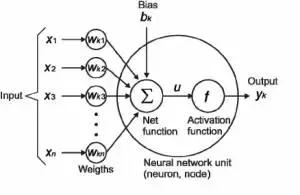
在下圖中，我們將"n"個輸入給定為 X1 到 Xn 而與其相應的權重為 Wk1 到 Wkn。我們有一個給定值為 bk 的偏差。權重首先乘以與其對應的輸入，然後與偏差加在一起。而這個值叫做 u。

U =ΣW*X +b

啟用函式被應用於 u，即 f(u)，並且我們會從神經元接收最終輸出，如 yk = f（u）。

• 常用的啟用函式

最常用的啟用函式就是 Sigmoid，ReLU 和 softmax

（a）Sigmoid——最常用的啟用函式之一是 Sigmoid，它被定義為：

sigmoid(x)=1/(1+e ^-x )

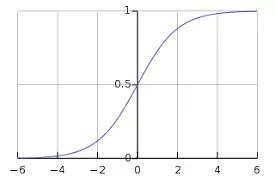
Sigmoid 變換產生一個值為 0 到 1 之間更平滑的範圍。我們可能需要觀察在輸入值略有變化時輸出值中發生的變化。光滑的曲線使我們能夠做到這一點，因此優於階躍函式。

（b）ReLU（整流線性單位）——與 Sigmoid 函式不同的是，最近的網路更喜歡使用 ReLu 啟用函式來處理隱藏層。該函式定義為：

f(x)=max(x,0)

當 X>0 時，函式的輸出值為 X；當 X<=0 時，輸出值為 0。函式圖如下圖所示：

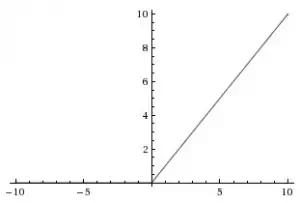
使用 ReLU 函式的最主要的好處是對於大於 0 的所有輸入來說，它都有一個不變的導數值。常數導數值有助於網路訓練進行得更快。

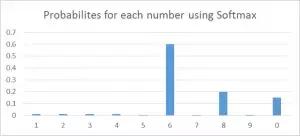
（c） Softmax——Softmax 啟用函式通常用於輸出層，用於分類問題。它與 sigmoid 函式是很類似的，唯一的區別就是輸出被歸一化為總和為 1。Sigmoid 函式將發揮作用以防我們有一個二進位制輸出，但是如果我們有一個多類分類問題，softmax 函式使為每個類分配值這種操作變得相當簡單，而這可以將其解釋為概率。

以這種方式來操作的話，我們很容易看到——假設你正在嘗試識別一個可能看起來像 8 的 6。該函式將為每個數字分配值如下。我們可以很容易地看出，最高概率被分配給 6，而下一個最高概率分配給 8，依此類推……

5、神經網路（Neural Network）——神經網路構成了深度學習的支柱。神經網路的目標是找到一個未知函式的近似值。它由相互聯絡的神經元形成。這些神經元具有權重和在網路訓練期間根據錯誤來進行更新的偏差。啟用函式將非線性變換置於線性組合，而這個線性組合稍後會生成輸出。啟用的神經元的組合會給出輸出值。

• 一個很好的神經網路定義：

"神經網路由許多相互關聯的概念化的人造神經元組成，它們之間傳遞相互資料，並且具有根據網路"經驗"調整的相關權重。神經元具有啟用閾值，如果通過其相關權重的組合和傳遞給他們的資料滿足這個閾值的話，其將被解僱;發射神經元的組合導致"學習"。

6、輸入/輸出/隱藏層（Input / Output / Hidden Layer）——正如它們名字所代表的那樣，輸入層是接收輸入那一層，本質上是網路的第一層。而輸出層是生成輸出的那一層，也可以說是網路的最終層。處理層是網路中的隱藏層。這些隱藏層是對傳入資料執行特定任務並將其生成的輸出傳遞到下一層的那些層。輸入和輸出層是我們可見的，而中間層則是隱藏的。

7、MLP（多層感知器）——單個神經元將無法執行高度複雜的任務。因此，我們使用堆疊的神經元來生成我們所需要的輸出。在最簡單的網路中，我們將有一個輸入層、一個隱藏層和一個輸出層。每個層都有多個神經元，並且每個層中的所有神經元都連線到下一層的所有神經元。這些網路也可以被稱為完全連線的網路。

8、正向傳播（Forward Propagation）——正向傳播是指輸入通過隱藏層到輸出層的運動。在正向傳播中，資訊沿著一個單一方向前進。輸入層將輸入提供給隱藏層，然後生成輸出。這過程中是沒有反向運動的。

9、成本函式（Cost Function）——當我們建立一個網路時，網路試圖將輸出預測得儘可能靠近實際值。我們使用成本/損失函式來衡量網路的準確性。而成本或損失函式會在發生錯誤時嘗試懲罰網路。

我們在執行網路時的目標是提高我們的預測精度並減少誤差，從而最大限度地降低成本。最優化的輸出是那些成本或損失函式值最小的輸出。

如果我將成本函式定義為均方誤差，則可以寫為：

C= 1/m ∑(y–a)^2，

其中 m 是訓練輸入的數量，a 是預測值，y 是該特定示例的實際值。

學習過程圍繞最小化成本來進行。

10、梯度下降（Gradient Descent）——梯度下降是一種最小化成本的優化演算法。要直觀地想一想，在爬山的時候，你應該會採取小步驟，一步一步走下來，而不是一下子跳下來。因此，我們所做的就是，如果我們從一個點 x 開始，我們向下移動一點，即Δh，並將我們的位置更新為 x-Δh，並且我們繼續保持一致，直到達到底部。考慮最低成本點。

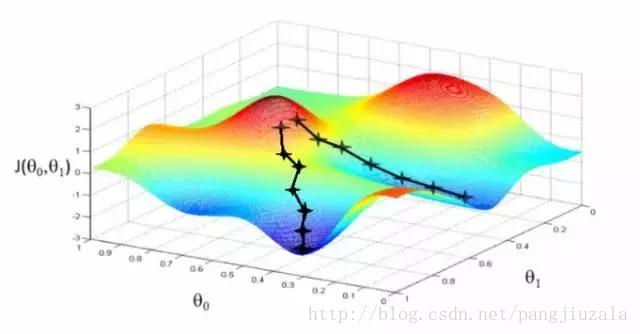
在數學上，為了找到函式的區域性最小值，我們通常採取與函式梯度的負數成比例的步長。

11、學習率（Learning Rate）——學習率被定義為每次迭代中成本函式中最小化的量。簡單來說，我們下降到成本函式的最小值的速率是學習率。我們應該非常仔細地選擇學習率，因為它不應該是非常大的，以至於最佳解決方案被錯過，也不應該非常低，以至於網路需要融合。

12、反向傳播（Backpropagation）——當我們定義神經網路時，我們為我們的節點分配隨機權重和偏差值。一旦我們收到單次迭代的輸出，我們就可以計算出網路的錯誤。然後將該錯誤與成本函式的梯度一起反饋給網路以更新網路的權重。 最後更新這些權重，以便減少後續迭代中的錯誤。使用成本函式的梯度的權重的更新被稱為反向傳播。

在反向傳播中，網路的運動是向後的，錯誤隨著梯度從外層通過隱藏層流回，權重被更新。

13、批次（Batches）——在訓練神經網路的同時，不用一次傳送整個輸入，我們將輸入分成幾個隨機大小相等的塊。與整個資料集一次性饋送到網路時建立的模型相比，批量訓練資料使得模型更加廣義化。

14、週期（Epochs）——週期被定義為向前和向後傳播中所有批次的單次訓練迭代。這意味著 1 個週期是整個輸入資料的單次向前和向後傳遞。

你可以選擇你用來訓練網路的週期數量，更多的週期將顯示出更高的網路準確性，然而，網路融合也需要更長的時間。另外，你必須注意，如果週期數太高，網路可能會過度擬合。

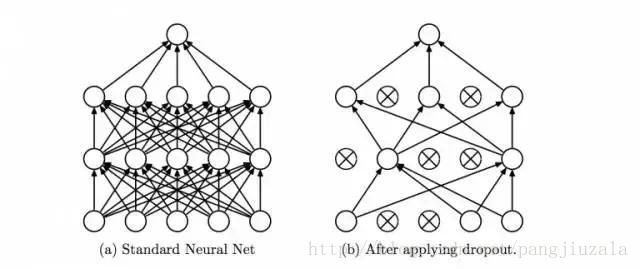
15、丟棄（Dropout）——Dropout 是一種正則化技術，可防止網路過度擬合套。顧名思義，在訓練期間，隱藏層中的一定數量的神經元被隨機地丟棄。這意味著訓練發生在神經網路的不同組合的神經網路的幾個架構上。你可以將 Dropout 視為一種綜合技術，然後將多個網路的輸出用於產生最終輸出。

16、批量歸一化（Batch Normalization）——作為一個概念，批量歸一化可以被認為是我們在河流中設定為特定檢查點的水壩。這樣做是為了確保資料的分發與希望獲得的下一層相同。當我們訓練神經網路時，權重在梯度下降的每個步驟之後都會改變，這會改變資料的形狀如何傳送到下一層。

但是下一層預期分佈類似於之前所看到的分佈。 所以我們在將資料傳送到下一層之前明確規範化資料。

卷積神經網路

17、濾波器（Filters）——CNN 中的濾波器與加權矩陣一樣，它與輸入影象的一部分相乘以產生一個迴旋輸出。我們假設有一個大小為 28 28 的影象，我們隨機分配一個大小為 3 3 的濾波器，然後與影象不同的 3 * 3 部分相乘，形成所謂的卷積輸出。濾波器尺寸通常小於原始影象尺寸。在成本最小化的反向傳播期間，濾波器值被更新為重量值。

參考一下下圖，這裡 filter 是一個 3 * 3 矩陣：

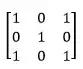
與影象的每個 3 * 3 部分相乘以形成卷積特徵。

18、卷積神經網路（CNN）——卷積神經網路基本上應用於影象資料。假設我們有一個輸入的大小（28 28 3），如果我們使用正常的神經網路，將有 2352（28 28 3）引數。並且隨著影象的大小增加引數的數量變得非常大。我們"卷積"影象以減少引數數量（如上面濾波器定義所示）。當我們將濾波器滑動到輸入體積的寬度和高度時，將產生一個二維啟用圖，給出該濾波器在每個位置的輸出。我們將沿深度尺寸堆疊這些啟用圖，併產生輸出量。

你可以看到下面的圖，以獲得更清晰的印象。

19、池化（Pooling）——通常在卷積層之間定期引入池層。這基本上是為了減少一些引數，並防止過度擬合。最常見的池化型別是使用 MAX 操作的濾波器尺寸（2,2）的池層。它會做的是，它將佔用原始影象的每個 4 * 4 矩陣的最大值。

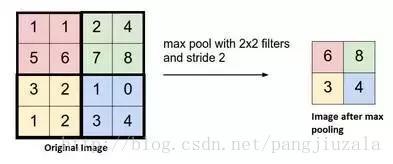
你還可以使用其他操作（如平均池）進行池化，但是最大池數量在實踐中表現更好。

20、填充（Padding）——填充是指在影象之間新增額外的零層，以使輸出影象的大小與輸入相同。這被稱為相同的填充。

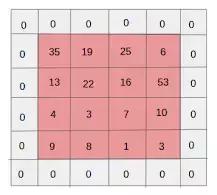
在應用濾波器之後，在相同填充的情況下，卷積層具有等於實際影象的大小。

有效填充是指將影象保持為具有實際或"有效"的影象的所有畫素。在這種情況下，在應用濾波器之後，輸出的長度和寬度的大小在每個卷積層處不斷減小。

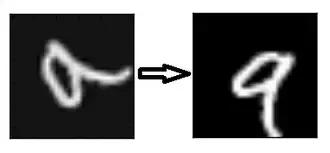
21、資料增強（Data Augmentation）——資料增強是指從給定資料匯出的新資料的新增，這可能被證明對預測有益。例如，如果你使光線變亮，可能更容易在較暗的影象中看到貓，或者例如，數字識別中的 9 可能會稍微傾斜或旋轉。在這種情況下，旋轉將解決問題並提高我們的模型的準確性。通過旋轉或增亮，我們正在提高資料的質量。這被稱為資料增強。

迴圈神經網路

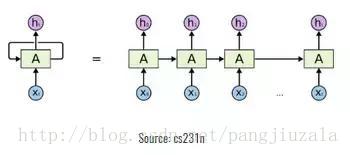
22、迴圈神經元（Recurrent Neuron）——迴圈神經元是在 T 時間內將神經元的輸出傳送回給它。如果你看圖，輸出將返回輸入 t 次。展開的神經元看起來像連線在一起的 t 個不同的神經元。這個神經元的基本優點是它給出了更廣義的輸出。

23、迴圈神經網路（RNN）——迴圈神經網路特別用於順序資料，其中先前的輸出用於預測下一個輸出。在這種情況下，網路中有迴圈。隱藏神經元內的迴圈使他們能夠儲存有關前一個單詞的資訊一段時間，以便能夠預測輸出。隱藏層的輸出在 t 時間戳內再次傳送到隱藏層。展開的神經元看起來像上圖。只有在完成所有的時間戳後，迴圈神經元的輸出才能進入下一層。傳送的輸出更廣泛，以前的資訊保留的時間也較長。

然後根據展開的網路將錯誤反向傳播以更新權重。這被稱為通過時間的反向傳播（BPTT）。

24、消失梯度問題（Vanishing Gradient Problem）——啟用函式的梯度非常小的情況下會出現消失梯度問題。在權重乘以這些低梯度時的反向傳播過程中，它們往往變得非常小，並且隨著網路進一步深入而"消失"。這使得神經網路忘記了長距離依賴。這對迴圈神經網路來說是一個問題，長期依賴對於網路來說是非常重要的。

這可以通過使用不具有小梯度的啟用函式 ReLu 來解決。

25、激增梯度問題（Exploding Gradient Problem）——這與消失的梯度問題完全相反，啟用函式的梯度過大。在反向傳播期間，它使特定節點的權重相對於其他節點的權重非常高，這使得它們不重要。這可以通過剪下梯度來輕鬆解決，使其不超過一定值