傳紙條（一）
時間限制：2000 ms | 記憶體限制：65535 KB
難度：5
描述
小淵和小軒是好朋友也是同班同學，他們在一起總有談不完的話題。一次素質拓展活動中，班上同學安排做成一個m行n列的矩陣，而小淵和小軒被安排在矩陣對角線的兩端，因此，他們就無法直接交談了。幸運的是，他們可以通過傳紙條來進行交流。紙條要經由許多同學傳到對方手裡，小淵坐在矩陣的左上角，座標(1,1)，小軒坐在矩陣的右下角，座標(m,n)。從小淵傳到小軒的紙條只可以向下或者向右傳遞，從小軒傳給小淵的紙條只可以向上或者向左傳遞。

在活動進行中，小淵希望給小軒傳遞一張紙條，同時希望小軒給他回覆。班裡每個同學都可以幫他們傳遞，但只會幫他們一次，也就是說如果此人在小淵遞給小軒紙條的時候幫忙，那麼在小軒遞給小淵的時候就不會再幫忙。反之亦然。

還有一件事情需要注意，全班每個同學願意幫忙的好感度有高有低（注意：小淵和小軒的好心程度沒有定義，輸入時用0表示），可以用一個0-1000的自然數來表示，數越大表示越好心。小淵和小軒希望儘可能找好心程度高的同學來幫忙傳紙條，即找到來回兩條傳遞路徑，使得這兩條路徑上同學的好心程度之和最大。現在，請你幫助小淵和小軒找到這樣的兩條路徑。

輸入
第一行輸入N(0< N< 100)表示待測資料組數。
每組測試資料輸入的第一行有2個用空格隔開的整數m和n，表示班裡有m行n列（2<=m,n<=50）。
接下來的m行是一個m*n的矩陣，矩陣中第i行j列的整數表示坐在第i行j列的學生的好心程度（不大於1000）。每行的n個整數之間用空格隔開。
輸出
每組測試資料輸出共一行，包含一個整數，表示來回兩條路上參與傳遞紙條的學生的好心程度之和的最大值。
樣例輸入
1
3 3
0 3 9
2 8 5
5 7 0
樣例輸出
34

分析：
題目要求從1,1到m,n兩條不向交的路徑的權值和最大值。我們可以把問題轉化為有兩個人同時從1,1向m,n走，兩人不相交。由於兩人可以走所有的格子，所以我們分別用x1,y1,x2,y2來表示某一時刻兩人的位置。所以我們要用一個4維的陣列來表示出所有的狀態。
那麼狀態是怎麼樣轉移的呢？

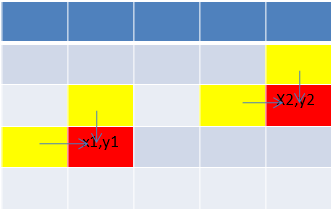
如圖所示：由於只能向下或者向右走，所以（x1，y1）,(x2,y2)分別可以由圖中黃色部分走一步得到。從上一步到這一步總共有4種情況。所以狀態轉移方為：(a[][]存權值）
dp[x1][y1][x2][y2]=max(dp[x1][y1-1][x2][y2-1],dp[x1][y1-1],x2-1][y2],dp[x1-1][y1][x2][y2-1],dp[x1-1][y1][x2-1][y2])+a[x1][y1]+a[x2][y2];

時間複雜度為O(n^4)；
優化：
我們令k表示走過的步數，所以有x1+y1=k,x2+y2=k(初始時k=1+1);知道了k,x1,x2,那麼我們就可以知道y1,y2了。所以狀態可以降低為3維，狀態轉移方程：
dp[k][x1][x2]=max(dp[k-1][x1-1][x2],dp[k-1][x1-1][x2-1],dp[k-1][x1][x2],dp[k-1][x1][x2-1])+a[x1][k-x1]+a[x2][k-x2];

注意：在實現的過程中,當x1==x2時說明兩個人相交了，要排除。所以我們的結束狀態並不是兩個人都到達了（m,n）而是在（m,n）的左邊和上上面。k的範圍為2~n+m-1,最終結束時為：dp[n+m-1][m][m-1];

AC程式碼：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>

using namespace std;

int const N = 55;
int a[N][N];
int dp[2*N][N][N];
int m,n;

int max_4(int a,int b,int c,int d)
{
    return max(max(a,b),max(c,d));
}

int max_path()
{
    for(int k=2;k<=n+m-1;k++)//開始時x1+y1=2 ,結束時x1+y1=n+m-1;
    {
        for(int x1=1;x1<=m;x1++)
        {
            for(int x2=1;x2<=m;x2++)
            {
                if(x1==x2) continue;//注意
                dp[k][x1][x2]=max_4(dp[k-1][x1][x2],dp[k-1][x1-1][x2],dp[k-1][x1][x2-1],dp[k-1][x1-1][x2-1])+a[x1][k-x1]+a[x2][k-x2];
            }
        }
    }
    return dp[m+n-1][m][m-1];
}

int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&m,&n);
        memset(dp,0,sizeof(dp));
        for(int i=1;i<=m;i++)
        {
            for(int j=1;j<=n;j++)
            {
                scanf("%d",&a[i][j]);
            }
        }
        printf("%d\n",max_path());
    }
    return 0;
}