2. 程式人生 > >樹狀陣列 資料結構詳解與模板(可能是最詳細的了)

樹狀陣列 資料結構詳解與模板(可能是最詳細的了)

阿新 • • 發佈：2019-02-15

目錄

單點更新:

區間查詢:

高階操作

求逆序對

操作

原理

查詢

修改

查詢

修改

樹狀陣列基礎

樹狀陣列是一個查詢和修改複雜度都為log(n)的資料結構。主要用於陣列的單點修改&&區間求和.

另外一個擁有類似功能的是線段樹.

具體區別和聯絡如下：

1.兩者在複雜度上同級, 但是樹狀陣列的常數明顯優於線段樹, 其程式設計複雜度也遠小於線段樹.

2.樹狀陣列的作用被線段樹完全涵蓋, 凡是可以使用樹狀陣列解決的問題, 使用線段樹一定可以解決, 但是線段樹能夠解決的問題樹狀陣列未必能夠解決.

3.樹狀陣列的突出特點是其程式設計的極端簡潔性, 使用lowbit技術可以在很短的幾步操作中完成樹狀陣列的核心操作，其程式碼效率遠高於線段樹。

上面出現了一個新名詞:lowbit.其實lowbit(x)就是求x最低位的1;

下面加圖進行解釋

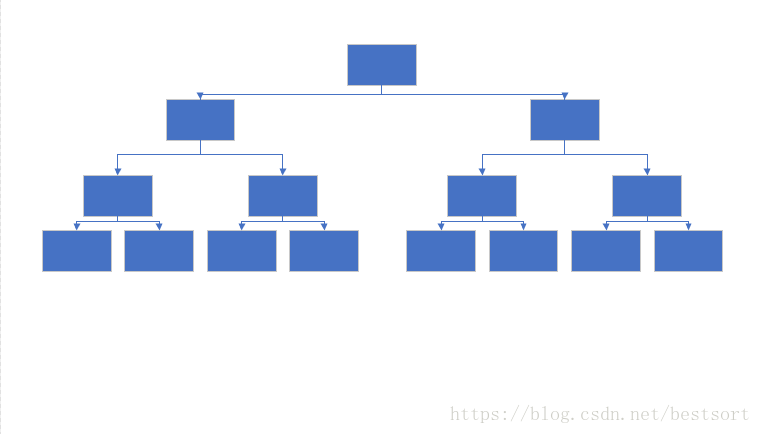
對於一般的二叉樹,我們是這樣畫的

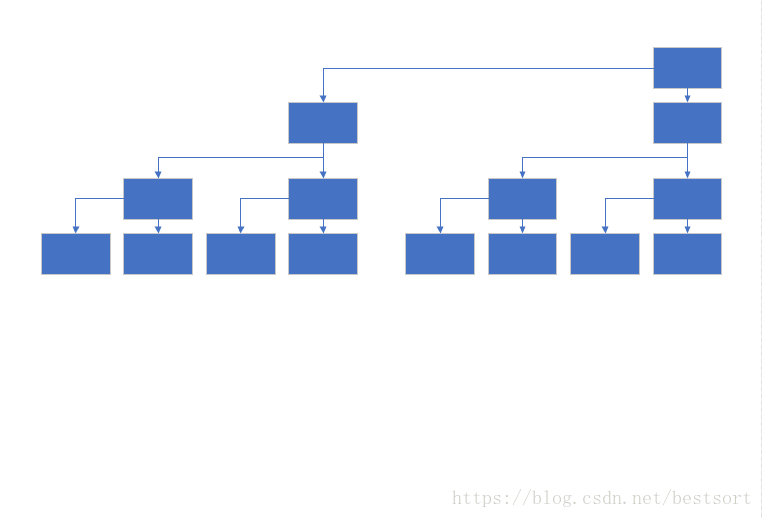
把位置稍微移動一下,便是樹狀陣列的畫法

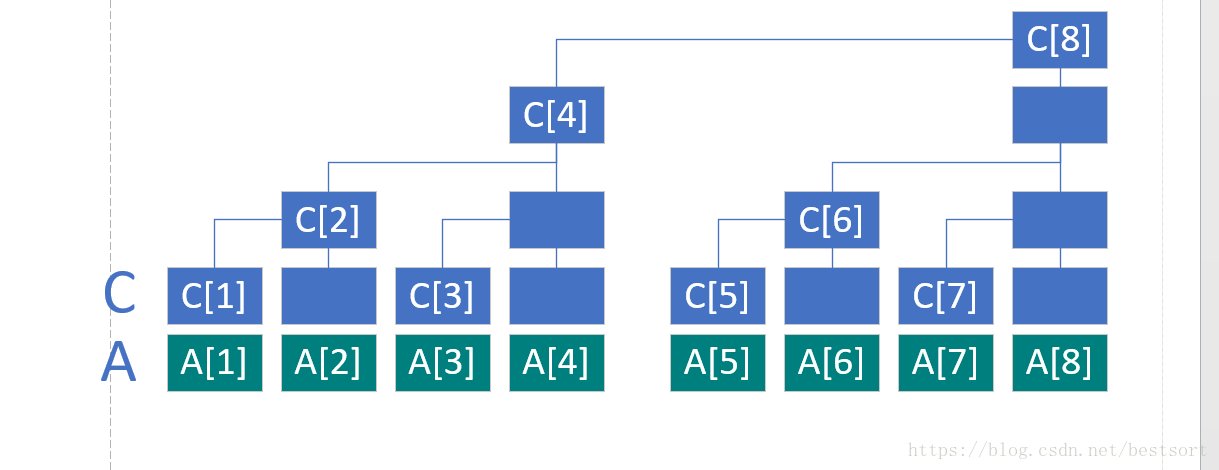
上圖其實是求和之後的陣列,原陣列和求和陣列的對照關係如下,其中a陣列是原陣列,c陣列是求和後的陣列:

C[i]代表 子樹的葉子結點的權值之和

如圖可以知道

C[1]=A[1];

C[2]=A[1]+A[2];

C[3]=A[3];

C[4]=A[1]+A[2]+A[3]+A[4];

C[5]=A[5];

C[6]=A[5]+A[6];

C[7]=A[7];

C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

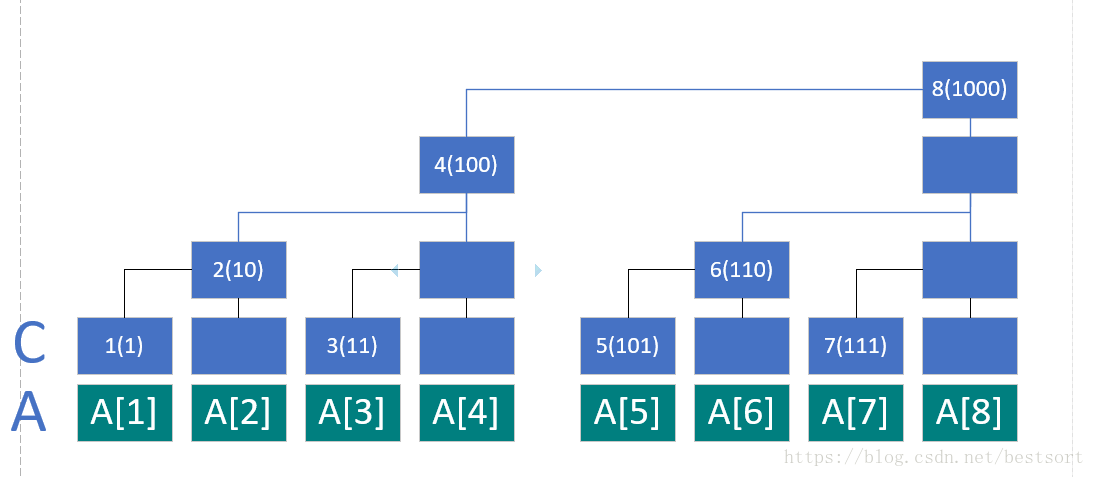
再將其轉化為二進位制看一下:

        C[1] = C[0001] = A[1];

        C[2] = C[0010] = A[1]+A[2];

        C[3] = C[0011] = A[3];

        C[4] = C[0100] = A[1]+A[2]+A[3]+A[4];

        C[5] = C[0101] = A[5];

        C[6] = C[0110] = A[5]+A[6];

        C[7] = C[0111] = A[7];

        C[8] = C[1000] = A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

對照式子可以發現  C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i]; （k為i的二進位制中從最低位到高位連續零的長度）例如i=8(1000)時，k=3;

C[8] = A[8-2^3+1]+A[8-2^3+2]+......+A[8]

即為上面列出的式子

現在我們返回到lowbit中來

其實不難看出lowbit(i)便是上面的2^k

因為2^k後面一定有k個0

比如說2^5==>100000

正好是i最低位的1加上字尾0所得的值

開篇就說了,lowbit(x)是取出x的最低位1;具體操作為

int lowbit(x){return x&(-x);}

極致簡短!!!!現在我們來理解一下這行程式碼:

我們知道,對於一個數的負數就等於對這個數取反+1

以二進位制數11010為例:11010的補碼為00101,加1後為00110,兩者相與便是最低位的1

其實很好理解,補碼和原碼必然相反,所以原碼有0的部位補碼全是1,補碼再+1之後由於進位那麼最末尾的1和原碼

最右邊的1一定是同一個位置(當遇到第一個1的時候補碼此位為0,由於前面會進一位,所以此位會變為1)

所以我們只需要進行a&(-a)就可以取出最低位的1了

會了lowbit,我們就可以進行區間查詢和單點更新了!!!

--------------------------------------------------------------------------------------------

單點更新:

繼續看開始給出的圖

此時如果我們要更改A[1]

則有以下需要進行同步更新

1(001)        C[1]+=A[1]

lowbit(1)=001 1+lowbit(1)=2(010)     C[2]+=A[1]

lowbit(2)=010 2+lowbit(2)=4(100)     C[4]+=A[1]

lowbit(4)=100 4+lowbit(4)=8(1000)   C[8]+=A[1]

換成程式碼就是:

void update(int x,int y,int n){
    for(int i=x;i<=n;i+=lowbit(i))    //x為更新的位置,y為更新後的數,n為陣列最大值
        c[i] += y;
}

--------------------------------------------------------------------------------------------

區間查詢:

舉個例子 i=5

C[4]=A[1]+A[2]+A[3]+A[4]; 

C[5]=A[5];

可以推出:   sum(i = 5)  ==> C[4]+C[5];

序號寫為二進位制: sum(101)=C[(100)]+C[(101)];

第一次101,減去最低位的1就是100;

其實也就是單點更新的逆操作

程式碼如下:

int getsum(int x){
    int ans = 0;
    for(int i=x;i;i-=lowbit(i))
        ans += c[i];
    return ans;
}

lowbit會了,區間查詢有了,單點更新也有了接下來該做題了

附程式碼:

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <queue>
#include <string>
#include <vector>
#define For(a,b) for(int a=0;a<b;a++)
#define mem(a,b) memset(a,b,sizeof(a))
#define _mem(a,b) memset(a,0,(b+1)<<2)
#define lowbit(a) ((a)&-(a))
using namespace std;
typedef long long ll;
const int maxn =  5*1e4+5;
const int INF = 0x3f3f3f3f;
int c[maxn];
void update(int x,int y,int n){
    for(int i=x;i<=n;i+=lowbit(i))
        c[i] += y;
}
int getsum(int x){
    int ans = 0;
    for(int i=x;i;i-=lowbit(i))
        ans += c[i];
    return ans;
}
int main()
{
    int t;
    int n;
    int x,y,z;
    string s;
    cin >> t ;
    for(int j=1;j<=t;j++){
        scanf("%d",&n);
        _mem(c,n);      //初始化陣列中前n+1個數為0
        for(int i=1;i<=n;i++){
            scanf("%d",&z);
            update(i,z,n);
        }
        cout <<"Case "<<j<<":"<<endl;
        while(1){
            cin >> s;
            if(s[0] == 'E')
                break;
            scanf("%d%d",&x,&y);
            if(s[0] == 'Q')
                cout << getsum(y)-getsum(x-1)<<endl;
            else if(s[0] == 'A')
                update(x,y,n);
            else
                update(x,-y,n);
        }
    }
    return 0;
}

高階操作

求逆序對

操作

對於陣列a，我們將其離散化處理為b[].區間查詢與單點修改程式碼如下

void update(int p)
{
    while(p<=n)
    {
        a[p] ++;
        p+=lowbit(p);
    }
}

int getsum(int p)
{
    int res = 0;
    while(p)
        res += a[p],p -= lowbit(p);
    return res;
}

a的逆序對個數為：

for(int i=1;i<=n;i++){
    update(b[i]+1);
    res += i-getsum(b[i]+1);
}

res就是逆序對個數，ask，需注意b[i]應該大於0

原理

第一次插入的時候把5這個位置上加上1，read(x)值就是1，當前已經插入了一個數，所以他前面比他大的數的個數就等於 i - read(x) = 1 - 1 = 0，所以總數 sum += 0

第二次插入的時候，read(x)的值同樣是1，但是 i - read(x) = 2 - 1 = 1，所以sum += 1

第三次的時候，read(x)的值是2，i - read(x) = 3 - 2 = 1，所以sum += 1

第四次，read(x)的值是1，i - read(x) = 4 - 1 = 3，所以sum += 3

第五次，read(x)的值是1，i - read(x) = 5 - 1 = 4，所以sum += 4

這樣整個過程就結束了，所有的逆序對就求出來了。

求區間最大值

void Update(int i,int v)
{
    while(i<=maxY)
    {
        t[i] = max(t[i],v);
        i += lowbit(i);
    }
}
int query(int i)
{
    int ans = 0;
    while(i)
    {
        ans = max(ans,t[i]);
        i -= lowbit(i);
    }
    return ans;
}

區間修改+單點查詢

通過“差分”（就是記錄陣列中每個元素與前一個元素的差），可以把這個問題轉化為問題1。

查詢

設原陣列為a[i], 設陣列d[i]=a[i]-a[i-1](a[0]=0)，則a[i]=\sum_{j=1}^{i}d[j]，可以通過求d[i]的字首和查詢。

修改

當給區間[l,r]加上x的時候，a[l]與前一個元素 a[l-1]的差增加了x，a[r+1]與 a[r]的差減少了x。根據d[i]陣列的定義，只需給a[l]加上 x, 給 a[r+1]減去x即可

void add(int p, int x){ //這個函式用來在樹狀陣列中直接修改
    while(p <= n) sum[p] += x, p += p & -p;
}
void range_add(int l, int r, int x){ //給區間[l, r]加上x
    add(l, x), add(r + 1, -x);
}
int ask(int p){ //單點查詢
    int res = 0;
    while(p) res += sum[p], p -= p & -p;
    return res;
}

區間修改+區間查詢

這是最常用的部分，也是用線段樹寫著最麻煩的部分——但是現在我們有了樹狀陣列！

怎麼求呢？我們基於問題2的“差分”思路，考慮一下如何在問題2構建的樹狀陣列中求字首和：

位置p的字首和 =\sum_{i=1}^{p}a[i]=\sum_{i=1}^{p}\sum_{j=1}^{i}d[j]

在等式最右側的式子\sum_{i=1}^{p}\sum_{j=1}^{i}d[j]中，d[1]被用了p次，d[2]被用了p-1次……那麼我們可以寫出：

位置p的字首和 =\sum_{i=1}^{p}\sum_{j=1}^{i}d[j]=\sum_{i=1}^{p}d[i]*(p-i+1)=(p+1)*\sum_{i=1}^{p}d[i]-\sum_{i=1}^{p}d[i]*i

那麼我們可以維護兩個陣列的字首和：
一個數組是 sum1[i]=d[i]
另一個數組是 sum2[i]=d[i]*i

查詢

位置p的字首和即：(p+1)*sum1陣列中p的字首和 - sum2陣列中p的字首和。

區間[l, r]的和即：位置r的字首和 - 位置l的字首和。

修改

對於sum1陣列的修改同問題2中對d陣列的修改。

對於sum2陣列的修改也類似，我們給 sum2[l] 加上 l * x，給 sum2[r + 1] 減去 (r + 1) * x。

void add(ll p, ll x){
    for(int i = p; i <= n; i += i & -i)
        sum1[i] += x, sum2[i] += x * p;
}
void range_add(ll l, ll r, ll x){
    add(l, x), add(r + 1, -x);
}
ll ask(ll p){
    ll res = 0;
    for(int i = p; i; i -= i & -i)
        res += (p + 1) * sum1[i] - sum2[i];
    return res;
}
ll range_ask(ll l, ll r){
    return ask(r) - ask(l - 1);
}

用這個做區間修改區間求和的題，無論是時間上還是空間上都比帶lazy標記的線段樹要優。

二維樹狀陣列

我們已經學會了對於序列的常用操作，那麼我們不由得想到（誰會想到啊喂）……能不能把類似的操作應用到矩陣上呢？這時候我們就要寫二維樹狀陣列了！

在一維樹狀陣列中，tree[x]（樹狀陣列中的那個“陣列”）記錄的是右端點為x、長度為lowbit(x)的區間的區間和。
那麼在二維樹狀陣列中，可以類似地定義tree[x][y]記錄的是右下角為(x, y)，高為lowbit(x), 寬為 lowbit(y)的區間的區間和。

單點修改+區間查詢

void add(int x, int y, int z){ //將點(x, y)加上z
    int memo_y = y;
    while(x <= n){
        y = memo_y;
        while(y <= n)
            tree[x][y] += z, y += y & -y;
        x += x & -x;
    }
}
void ask(int x, int y){//求左上角為(1,1)右下角為(x,y) 的矩陣和
    int res = 0, memo_y = y;
    while(x){
        y = memo_y;
        while(y)
            res += tree[x][y], y -= y & -y;
        x -= x & -x;
    }
}

區間修改 + 單點查詢

我們對於一維陣列進行差分，是為了使差分陣列字首和等於原陣列對應位置的元素。

那麼如何對二維陣列進行差分呢？可以針對二維字首和的求法來設計方案。

二維字首和：

sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j]

那麼我們可以令差分陣列d[i][j]表示a[i][j]與 a[i-1][j]+a[i][j-1]-a[i-1][j-1]的差。

例如下面這個矩陣

 1  4  8
 6  7  2
 3  9  5

對應的差分陣列就是

 1  3  4
 5 -2 -9
-3  5  1

當我們想要將一個矩陣加上x時，怎麼做呢？
下面是給最中間的3*3矩陣加上x時，差分陣列的變化：

0  0  0  0  0
0 +x  0  0 -x
0  0  0  0  0
0  0  0  0  0
0 -x  0  0 +x

這樣給修改差分，造成的效果就是：

0  0  0  0  0
0  x  x  x  0
0  x  x  x  0
0  x  x  x  0
0  0  0  0  0

那麼我們開始寫程式碼吧！

void add(int x, int y, int z){ 
    int memo_y = y;
    while(x <= n){
        y = memo_y;
        while(y <= n)
            tree[x][y] += z, y += y & -y;
        x += x & -x;
    }
}
void range_add(int xa, int ya, int xb, int yb, int z){
    add(xa, ya, z);
    add(xa, yb + 1, -z);
    add(xb + 1, ya, -z);
    add(xb + 1, yb + 1, z);
}
void ask(int x, int y){
    int res = 0, memo_y = y;
    while(x){
        y = memo_y;
        while(y)
            res += tree[x][y], y -= y & -y;
        x -= x & -x;
    }
}

區間修改 + 區間查詢

類比之前一維陣列的區間修改區間查詢，下面這個式子表示的是點(x, y)的二維字首和：

\sum_{i=1}^{x}\sum_{j=1}^{y}\sum_{k=1}^{i}\sum_{h=1}^{j}d[h][k]

(d[h][k]為點(h, k)對應的“二維差分”(同上題))

這個式子炒雞複雜(O(n^4) 複雜度！)，但利用樹狀陣列，我們可以把它優化到O(\log_2 n)！

首先，類比一維陣列，統計一下每個d[h][k]出現過多少次。d[1][1]出現了x*y次，d[1][2]出現了x*(y-1)次……d[h][k]出現了(x-h+1)*(y-k+1) 次。

那麼這個式子就可以寫成：

\sum_{i=1}^{x}\sum_{j=1}^{y}d[i][j]*(x+1-i)*(y+1-j)

把這個式子展開，就得到：

(x+1)*(y+1)*\sum_{i=1}^{x}\sum_{j=1}^{y}d[i][j]-(y+1)*\sum_{i=1}^{x}\sum_{j=1}^{y}d[i][j]*i-(x+1)*\sum_{i=1}^{x}\sum_{j=1}^{y}d[i][j]*j+\sum_{i=1}^{x}\sum_{j=1}^{y}d[i][j]*i*j

那麼我們要開四個樹狀陣列，分別維護：

d[i][j],d[i][j]*i,d[i][j]*j,d[i][j]*i*j

這樣就完成了！

#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
typedef long long ll;
ll read(){
    char c; bool op = 0;
    while((c = getchar()) < '0' || c > '9')
        if(c == '-') op = 1;
    ll res = c - '0';
    while((c = getchar()) >= '0' && c <= '9')
        res = res * 10 + c - '0';
    return op ? -res : res;
}
const int N = 205;
ll n, m, Q;
ll t1[N][N], t2[N][N], t3[N][N], t4[N][N];
void add(ll x, ll y, ll z){
    for(int X = x; X <= n; X += X & -X)
        for(int Y = y; Y <= m; Y += Y & -Y){
            t1[X][Y] += z;
            t2[X][Y] += z * x;
            t3[X][Y] += z * y;
            t4[X][Y] += z * x * y;
        }
}
void range_add(ll xa, ll ya, ll xb, ll yb, ll z){ //(xa, ya) 到 (xb, yb) 的矩形
    add(xa, ya, z);
    add(xa, yb + 1, -z);
    add(xb + 1, ya, -z);
    add(xb + 1, yb + 1, z);
}
ll ask(ll x, ll y){
    ll res = 0;
    for(int i = x; i; i -= i & -i)
        for(int j = y; j; j -= j & -j)
            res += (x + 1) * (y + 1) * t1[i][j]
                - (y + 1) * t2[i][j]
                - (x + 1) * t3[i][j]
                + t4[i][j];
    return res;
}
ll range_ask(ll xa, ll ya, ll xb, ll yb){
    return ask(xb, yb) - ask(xb, ya - 1) - ask(xa - 1, yb) + ask(xa - 1, ya - 1);
}
int main(){
    n = read(), m = read(), Q = read();
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++){
            ll z = read();
            range_add(i, j, i, j, z);
        }
    }
    while(Q--){
        ll ya = read(), xa = read(), yb = read(), xb = read(), z = read(), a = read();
        if(range_ask(xa, ya, xb, yb) < z * (xb - xa + 1) * (yb - ya + 1))
            range_add(xa, ya, xb, yb, a);
    }
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++)
            printf("%lld ", range_ask(i, j, i, j));
        putchar('\n');
    }
    return 0;
}

相關推薦

樹狀陣列 資料結構詳解與模板(可能是最詳細的了)

目錄 單點更新: 區間查詢: 高階操作 求逆序對 操作 原理 查詢 修改 查詢 修改 樹狀陣列基礎 樹狀陣列是一個查詢和修改複雜度都為log(n)的資料結構。主要用於陣列的單點修改&&區間求和

線段樹 資料結構詳解與模板

線段樹是一個查詢和修改複雜度都為log(n)的資料結構。主要用於陣列的單點修改&&單點查詢&&區間求和&&區間修改. 另外一個擁有類似功能的是樹狀陣列，但是樹狀陣列最常用的是單點修改&&區間求和. 線

Tire樹（字典樹）資料結構詳解（圖解）及模板

先在這裡放模板，具體圖解回去再發 #include <map> #include <queue> #include <cstdlib> #include <cm

hashmap資料結構詳解（五）之HashMap、HashTable、ConcurrentHashMap 的區別

【hashmap 與 hashtable】   hashmap資料結構詳解（一）之基礎知識奠基 hashmap資料結構詳解（二）之走進JDK原始碼 hashmap資料結構詳解（三）之hashcode例項及大小是2的冪次方解釋 hashmap資料結構詳解（四）之has

Redis內部資料結構詳解——intset

本文是《Redis內部資料結構詳解》系列的第七篇。在本文中，我們圍繞一個Redis的內部資料結構——intset展開討論。 Redis裡面使用intset是為了實現集合(set)這種對外的資料結構。set結構類似於數學上的集合的概念，它包含的元素無序，且不能重複。Redis裡的set結構還實現了

influxdb記憶體中Cache資料結構詳解

引: 前面TSM檔案格式解析（一到四）綜合分析了不同case下的TSM檔案格式，檔案格式已基本清楚。 寫入磁碟是如此格式，那在寫入磁碟之前的記憶體中是怎麼儲存的呢？ 通過第一篇influxdb初探https://blog.csdn.net/jacicson1987/article/det

資料結構有哪些，常用資料結構詳解

通過上節我們知道，資料結構是學習資料儲存方式的一門學科，那麼，資料儲存方式有哪幾種呢？本節將對資料結構的學習內容做一個簡要的總結。 資料結構大致包含以下幾種儲存結構： 線性表，還可細分為順序表、連結串列、棧和佇列； 樹結構，包括普通樹，二叉樹，線索二叉樹等； 圖儲存結構； 下面對各種資料結構做詳

[轉]Redis內部資料結構詳解-sds

本文是《Redis內部資料結構詳解》系列的第二篇，講述Redis中使用最多的一個基礎資料結構：sds。 不管在哪門程式語言當中，字串都幾乎是使用最多的資料結構。sds正是在Redis中被廣泛使用的字串結構，它的全稱是Simple Dynamic String。與其它語言環境中出現的字串相比，它具有如下顯著的

Redis內部資料結構詳解(1)——dict

如果你使用過Redis，一定會像我一樣對它的內部實現產生興趣。《Redis內部資料結構詳解》是我準備寫的一個系列，也是我個人對於之前研究Redis的一個階段性總結，著重講解Redis在記憶體中的資料結構實現（暫不涉及持久化的話題）。Redis本質上是一個數據結構伺服器（data st

Java資料結構詳解（十二）- HashMap

HashMap 基於雜湊表的 Map 介面的實現。此實現提供所有可選的對映操作，並允許使用 null 值和 null 鍵。（除了非同步和允許使用 null 之外，HashMap 類與 Hashtable 大致相同。）此類不保證對映的順序，特別是它不保證該順序恆

Java資料結構詳解（一）-Collection介面

Java資料結構-collection介面 一，Collection介面結構圖 Collection介面詳解 collection是一個被高度抽象出來的介面、提供基本的操作資料的行為、屬性的定義. collection api介紹： p

Redis資料結構詳解之List（二）

Redis中關於List列表的命令詳解  1、redis中list列表的資料插入命令：lpush，rpush，linsert 127.0.0.1:6379>rpush mylist 1   ---結果為：(integer) 1 127.0.0.1:6379&g

第123講：Hadoop叢集管理之Namenode目錄元資料結構詳解學習筆記

第123講：Hadoop叢集管理之Namenode目錄元資料結構詳解學習筆記 hadoop-2.x的叢集管理與hadoop-1.x有很大不同 hdfs-site.xml： dfs.replication dfs.namenode.name.dir  存放namenode元資

Redis內部資料結構詳解之整數集合(intset)

整數集合簡介 整數集合intset用於有序、無重複地儲存多個整數值，根據集合中元素的值自動選擇使用整數型別來儲存元素，例如：如果intset中絕對值最大的整數可以用int32_t來儲存，那麼整個

Redis資料結構詳解之Zset

Zset跟Set之間可以有並集運算，因為他們儲存的資料字串集合，不能有一樣的成員出現在一個zset中，但是為什麼有了set還要有zset呢？zset叫做有序集合，而set是無序的，zset怎麼做到有序的呢？就是zset的每一個成員都有一個分數與之對應，並且分數是

java中的資料結構詳解

也許你已經熟練使用了java.util包裡面的各種資料結構，但是我還是要說一說java版資料結構與演算法，希望對你有幫助。 線性表，連結串列，雜湊表是常用的資料結構，在進行Java開發時，JDK已經為我們提供了一系列相應的類來實現基本的資料結構。這些類均在java.ut

Redis內部資料結構詳解之字典(dict)

/* Expand or create the hash table */ int dictExpand(dict *d, unsigned long size) { dictht n; /* the new hash table */ unsigned long realsize = _di

Redis內部資料結構詳解(4)——ziplist

本文是《Redis內部資料結構詳解》系列的第四篇。在本文中，我們首先介紹一個新的Redis內部資料結構——ziplist，然後在文章後半部分我們會討論一下在robj, dict和ziplist的基礎上，Redis對外暴露的hash結構是怎樣構建起來的。 我們在討論中還會

Redis內部資料結構詳解之簡單動態字串(sds)

本文所引用的原始碼全部來自Redis2.8.2版本。 Redis中簡單動態字串sds資料結構與API相關檔案是：sds.h, sds.c。 預備知識 下面介紹有關sizeof計算引數

Redis資料結構詳解之Set（三）

序言 在Redis中，Set和list都是字串序列，非常相似，不同之處在於Set是用雜湊表來保持字串的唯一性，沒有先後順序，不像list一樣，可以在首尾增刪資料。但是set也有自己的相應處理命令來完成對自己的操作。下面我們來看下Set的命令怎麼使用。 操作單個set的