2. 程式人生 > >CNN for Visual Recognition（6）-lecture5預處理、正則化、損失函式

CNN for Visual Recognition（6）-lecture5預處理、正則化、損失函式

阿新 • • 發佈：2019-02-16

本節主要講了資料預處理、正則化以及損失函式

資料預處理

關於資料預處理我們有3種常用的方式，假設資料矩陣X，假設其尺寸是[N,D]（N是資料樣本的數量，D是資料的維度）。

去均值

去均值是預處理最常見的。對待訓練的每一張圖片的特徵，都減去全部訓練集圖片的特徵均值。它對資料中每個獨立特徵減去平均值，從幾何上可以理解為在每個維度上都將資料雲的中心都遷移到原點。在numpy中，該操作可以通過程式碼X -= np.mean(X, axis=0)實現。而對於影象，更常用的是對所有畫素都減去一個值，可以用X -= np.mean(X)實現，也可以在3個顏色通道上分別操作。

歸一化

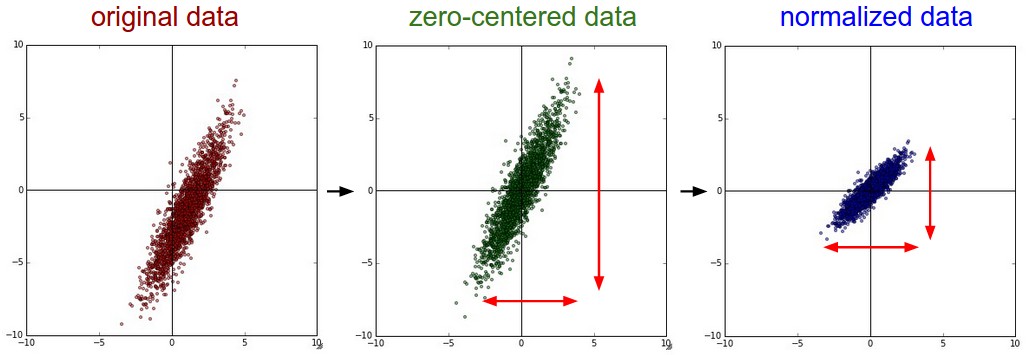
歸一化是將資料的所有維度都歸一化，使其數值範圍都近似相等。實現歸一化有兩種方式。第一種是先對資料做零中心化（zero-centered），也就是去均值處理，然後每個維度都除以其標準差，實現程式碼為X /= np.std(X, axis=0)。第二種是對每個維度都做歸一化，使得每個維度的最大和最小值是1和-1。這個預處理操作只有在確信不同的輸入特徵有不同的數值範圍（或計量單位）時才有意義，但要注意預處理操作的重要性幾乎等同於學習演算法本身。在影象處理中，由於畫素的數值範圍幾乎是一致的（0-255），所以進行此預處理不是必要的。

這裡寫圖片描述

PCA和白化

PCA和白化是另外一種資料預處理方式。在經過去均值操作之後，我們可以計算資料的協方差矩陣，從而可以知道資料各個維度之間的相關性。

# 假設輸入資料矩陣X的尺寸為[N x D]
X -= np.mean(X, axis = 0) # 對資料進行零中心化(重要)
cov = np.dot(X.T, X) / X.shape[0] # 得到資料的協方差矩陣

　　資料協方差矩陣的第i,j個元素是資料第i個和第j個維度的協方差。具體來說，該矩陣的對角線上的元素是方差。還有，協方差矩陣是對稱和半正定的。我們可以對資料協方差矩陣進行SVD（奇異值分解）運算。　　

U,S,V = np.linalg.svd(cov)

　　U的列是特徵向量，S是裝有奇異值的1維陣列（因為cov是對稱且半正定的，所以S中元素是特徵值的平方）。為了去除資料相關性，將已經零中心化處理過的原始資料投影到特徵基準上：

Xrot = np.dot(X,U) # 對資料去相關性

　　U是一組正交基向量。我們可以看做把原始資料X投射到這組維度保持不變的正交基底上，從而也就完成了對原始資料的去相關。如果去相關之後你再求一下Xrot的協方差矩陣，你會發現這時候的協方差矩陣是一個對角矩陣了。而numpy中的np.linalg.svd更好的一個特性是，它返回的U是對特徵值排序過的，這也就意味著，我們可以用它進行降維操作。我們可以只取top的一些特徵向量，然後做和原始資料做矩陣乘法，這個時候既降維減少了計算量，同時又儲存下了絕大多數的原始資料資訊，這就是主成分分析/PCA：

Xrot_reduced = np.dot(X, U[:,:100]) # Xrot_reduced 變成 [N x 100]

　　上面的程式碼，將原始的資料集由[N,D]降到了[N,100]，留下了資料中包含最大方差的100個維度。通常使用PCA降維過的資料訓練線性分類器和神經網路會達到非常好的效能效果，同時還能節省時間和儲存器空間。
　　白化（whitening）。白化操作的輸入是特徵基準上的資料，然後對每個維度除以其特徵值來對數值範圍進行歸一化。該變換的幾何解釋是：如果資料服從多變數的高斯分佈，那麼經過白化後，資料的分佈將會是一個均值為零，且協方差相等的矩陣。該操作的程式碼如下：

# 對資料進行白化操作:
# 除以特徵值 
Xwhite = Xrot / np.sqrt(S + 1e-5)

　　注意：增加噪聲。分母中添加了1e-5（或一個更小的常量）來防止分母為0。該變換的一個缺陷是在變換的過程中可能會增加資料中的噪聲，因為它將所有維度都拉伸到相同的數值範圍，這些維度中也包含了那些只有極少差異性(方差小)而大多是噪聲的維度。在實際操作中，這個問題可以用更強的平滑來解決（用比1e-5更大的值）。

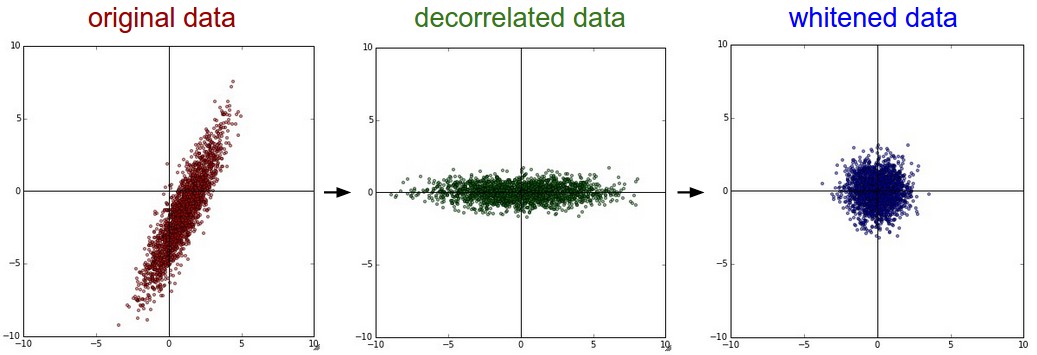
這裡寫圖片描述

　　上圖左邊是二維的原始資料。中間是經過PCA操作的資料。可以看出資料首先是零中心的，然後變換到了資料協方差矩陣的基準軸上。這樣就對資料進行去相關（協方差矩陣變成對角陣）。右邊：每個維度都被特徵值調整數值範圍，將資料協方差矩陣變為單位矩陣。從幾何上看，就是對資料在各個方向上拉伸壓縮，使之變成服從高斯分佈的一個數據點分佈。
　　下面我們以CIFAR-10資料集（50000*3072）為例，看看預處理的效果。

這裡寫圖片描述

　　圖片最左邊是原始的影象（49張）。
　　左二是一張圖3072個特徵值向量中的前144個。靠前面的特徵向量解釋了資料中大部分的方差，可見它們與影象中較低的頻率相關。
　　左三是49張經過了PCA降維處理的圖片，展示了前144個特徵向量。每個原始影象為3072維的向量，向量中的元素是圖片上某個位置的畫素在某個顏色通道中的亮度值。而現在僅使用了前144維的向量，每個元素表示了特徵向量對於組成這張圖片的貢獻度。為了讓圖片正常顯示，需要將144維度重新變成基於畫素基準的3072個數值進行視覺化。因為U是一個旋轉，可以通過乘以U.transpose()[:144,:]來實現。可以看見影象變得有點模糊了，這正好說明前面的特徵向量獲取了較低的頻率。可以看出，大多數資訊還是保留了下來。
　　最右邊影象是將“白化”後的資料進行顯示。其中144個維度中的方差都被壓縮到了相同的數值範圍。然後144個白化後的數值通過乘以U.transpose()[:144,:]轉換到影象畫素基準上。現在較低的頻率被隱去，突出了較高的頻率。
　　
　　實際上在卷積神經網路中並不會採用PCA和白化這些變換。然而對資料進行零中心化操作還是非常重要的，對每個畫素進行歸一化也很常見。

　　任何預處理策略（比如資料去均值）都只能在訓練集資料上進行計算，演算法訓練完畢後再應用到驗證集或者測試集上。例如，如果先計算整個資料集影象的平均值然後每張圖片都減去平均值，最後將整個資料集分成訓練/驗證/測試集，這個做法是錯誤的。應該先分成訓練/驗證/測試集，只是從訓練集中求圖片平均值，然後各個集（訓練/驗證/測試集）中的影象再減去這個平均值。

權重初始化

　　在開始訓練網路之前，還需要初始化網路的引數。
　　
　　錯誤：全零初始化。在訓練完畢後，雖然不知道網路中每個權重的最終值，但如果資料經過恰當的歸一化，就可以假設所有權重數值中大約一半為正數，一半為負數。這樣，有人會想把權重的初始值設為0，因為在期望上來說0是最合理的猜測。這個做法錯誤的！因為如果網路中的每個神經元都計算出同樣的輸出，然後它們就會在反向傳播中計算出同樣的梯度，從而進行同樣的引數更新。換句話說，如果權重被初始化為同樣的值，神經元之間就失去了不對稱性的源頭。
　　
　　不太好：小隨機數初始化。權重初始值最好非常接近0又不能等於0。解決方法就是將權重初始化為很小的數值，以此來打破對稱性。其思路是：如果神經元剛開始的時候是隨機且不相等的，那麼它們將計算出不同的更新，並將自身變成整個網路的不同部分。
　　小隨機數權重初始化的實現方法是：W = 0.01 * np.random.randn(fan_in,fan_out)。其中randn函式是基於零均值和標準差的一個高斯分佈來生成隨機數的。根據這個式子，每個神經元的權重向量都被初始化為一個隨機向量，而這些隨機向量又服從一個多變數高斯分佈，這樣在輸入空間中，所有的神經元的指向是隨機的。也可以使用均勻分佈生成的隨機數，但是從實踐結果來看，對於演算法的結果影響極小。
　　注意。並不是小數值一定會得到好的結果，可能會導致梯度飽和。例如，一個神經網路的層中的權重值很小，那麼在反向傳播的時候就會計算出非常小的梯度（因為梯度與權重值是成比例的）。這就會很大程度上減小反向傳播中的“梯度訊號”，在深度網路中，就會出現問題。
　　
　　正確：使用1/sqrt(n)校準方差（Xavier init）。小隨機數初始化存在一個問題，隨著輸入資料量的增長，隨機初始化的神經元的輸出資料的分佈中的方差也在增大。我們可以除以輸入資料量的平方根來調整其數值範圍，這樣神經元輸出的方差就歸一化到1了。也就是說，建議將神經元的權重向量初始化為：w = np.random.randn(fan_in,fan_out) / sqrt(fan_in)。其中fan_in是輸入資料的數量。這樣就保證了網路中所有神經元起始時有近似同樣的輸出分佈。實踐經驗證明，這樣做可以提高收斂的速度。
　　我們從數學的角度，簡單解釋一下，為什麼上述操作可以歸一化方差。考慮在激勵函式之前的權重w與輸入x的內積s=∑niwixi部分，我們計算一下s的方差：

Var(s)=Var(∑inwixi)=∑inVar(wixi)=∑in[E(wi)]2Var(xi)+E[(xi)]2Var(wi)+Var(xi)Var(wi)=∑inVar(xi)Var(wi)=(nVar(w))Var(x)

　　在前兩步，使用了方差的性質。在第三步，因為假設輸入和權重的平均值都是0，所以E[xi]=E[wi]=0。注意這只是假設，實際中比如ReLU單元中均值就為正。最後一步，我們假設所有的都服從同樣的分佈。從推導公式可見，如果想要s方差和輸入相同，那麼在初始化的時候必須保證每個權重w的方差是1/n。又因為對於一個隨機變數X和標量a，有Var(aX)=a2Var(X)，這就說明可以基於一個標準高斯分佈，然後乘以a=1/n−−−√，使其方差為1/n，於是得出：w = np.random.randn(n) / sqrt(n)。
　　
　　初始化權重還有一些其他的研究和建議，比如Glorot在論文Understanding the difficulty of training deep feedforward neural networks就推薦使用能滿足Var(w)=2/(nin+nout)的權重初始化。其中nin,nout是前一層和後一層的神經元個數。另外一篇比較新的論文Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification，指出尤其對於ReLU神經元，我們初始化方差應該為2.0/n，也就是w = np.random.randn(n) * sqrt(2.0/n)。目前的神經網路中使用了很多ReLU單元，因此推薦使用這個初始化方法。
　　
　　稀疏初始化（Sparse initialization）。此方法將所有權重矩陣設為0，同時為了打破對稱性，每個神經元都同下一層固定數目的神經元隨機連線（其權重數值由一個小的高斯分佈生成）。一個比較典型的連線數目是10個。
　　
　　偏置（biases）的初始化。通常將偏置初始化為0，這是因為隨機小數值權重矩陣已經打破了對稱性。對於ReLU非線性啟用函式，有研究人員喜歡使用如0.01這樣的小數值常量作為所有偏置的初始值，這是因為他們認為這樣做能讓所有的ReLU單元一開始就啟用，這樣就能儲存並傳播一些梯度。然而，這樣做並不清楚是否總是能提高演算法效能（有時實驗結果顯示效能更差），所以通常還是使用0來初始化偏置引數。
　　
　　批量歸一化（Batch Normalization）。該方法最近才提出，減輕瞭如何合理初始化神經網路這個棘手問題，其做法是讓啟用資料在訓練開始前通過一個網路，網路處理資料使其服從標準高斯分佈。因為歸一化是一個簡單可求導的操作，所以上述思路是可行的。在實現層面，應用這個技巧通常意味著全連線層（或者是卷積層）與啟用函式之間新增一個BatchNorm層。在實踐中，使用了批量歸一化的網路對於不好的初始值有更強的魯棒性。批量歸一化可以理解為在網路的每一層之前都做預處理。
　　

正則化Regularization

　　為了防止神經網路過擬合，有以下幾種正則化方法：