轉載請註明出處！

音訊重取樣作為一個獨立模組蘊含了數字訊號處理理論的多方面內容，綜合起來其物理原理及濾波器的實現優化可以作為一個獨立的專案做較深入的研究，可謂是一門學問。推薦大家研讀國外作者的理論研究工作，從數學模型到訊號處理細節講述的非常詳盡（需要具備一定的數字訊號處理基礎）。

言歸正傳，音訊重取樣分為上取樣和下采樣，即插值和抽取。在實現有理數級重取樣時，則是將上取樣和下采樣做結合（例如48kHz 轉 44.1kHz時，將44.1kHz近似為44kHz，將48kHz下采樣到4kHz，再上取樣至44kHz來實現）。

由數字訊號處理中，時域訊號和頻域訊號的時-頻對偶特性可知：時域的抽取，對應頻域的延拓；時域的插值，對應頻域的壓縮。如果對訊號的頻率成分不做限制的話，頻域的延拓可能會引發頻譜混迭；頻域的壓縮來引起頻譜映象相應。因此在下采樣前，要經過濾波器濾波來防止混迭，即抗混迭(antialiasing filter)濾波；上取樣後也要經過濾波處理，即抗映象(anti-image filter)濾波。

有延拓和映象特性可得：
下采樣( M )時所採用的濾波器截止頻率為Pi/M； 上取樣( L )時所採用的濾波器截止頻率為Pi/L. （可由時域訊號的取樣公式及傅立葉變換推匯出）。

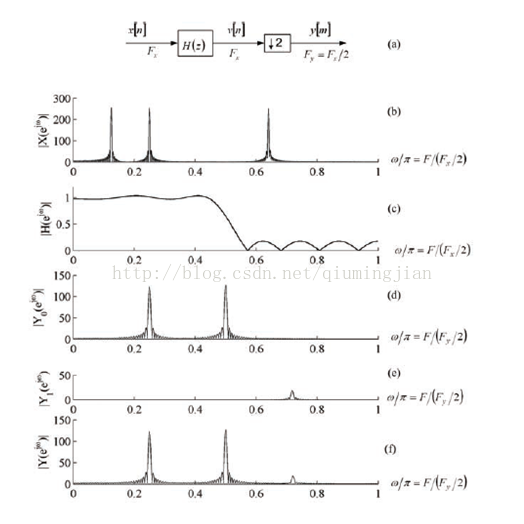
舉例實現下采樣： M=2，訊號頻率包含0.125Pi、0.25Pi和0.65Pi

下采過程如圖1所示：

圖1. 訊號下采樣示例（注：絕對理想濾波器不可實現）

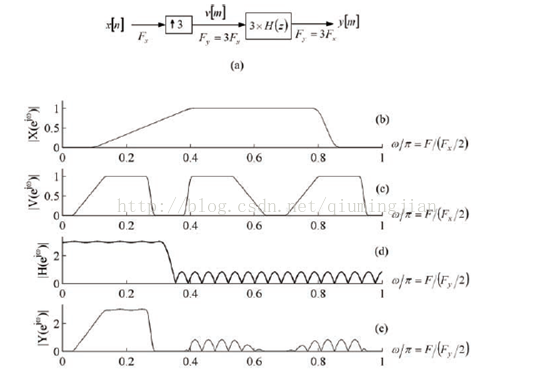
舉例實現下采樣： 頻域梯形， L=3

上採過程如圖2所示：

圖2. 訊號上取樣示例（注：絕對理想濾波器不可實現）