[LeetCode]*84.Largest Rectangle in Histogram
阿新 • • 發佈:2019-02-16
題目
Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.
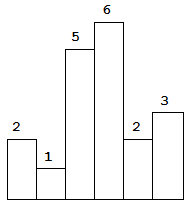
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].
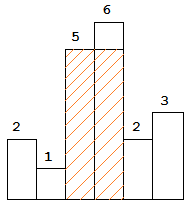
The largest rectangle is shown in the shaded area, which has area = 10 unit.
For example,
Given height = [2,1,5,6,2,3],
return 10.
思路
我們通過一個棧記錄上升的柱子,如果如果下降的柱子,可以開始計算棧頂和之前柱子構建的矩形的面積。棧儲存的是柱子的下標,而不是柱子的高度,目的是方便計算矩形的面積。遇到上升的柱子,就把柱子對應的下標壓入棧。
程式碼
/*---------------------------------------
* 日期:2015-05-13
* 作者:SJF0115
* 題目: 84.Largest Rectangle in Histogram
* 網址:https://leetcode.com/problems/largest-rectangle-in-histogram/
* 結果:AC
* 來源:LeetCode
* 部落格:
-----------------------------------------*/ 執行時間