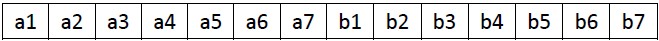給定一個數組a1,a2,a3,...an,b1,b2,b3..bn,最終把它置換成a1,b1,a2,b2,...an,bn。

分析：

本題是完美洗牌問題的變形。

完美洗牌問題：   給定一個數組a1,a2,a3,...an,b1,b2,b3..bn,最終把它置換成b1,a1,b2,a2,...bn,an。

我們先解決完美洗牌問題。

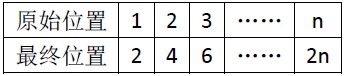
為方便起見，我們考慮的是一個下標從1開始的陣列，下標範圍是[1..2n]。 我們看一下每個元素最終去了什麼地方。

前n個元素 a1 -> a2  a2->a4.... 第i個元素去了 第（2 * i）的位置。

後n個元素a(n + 1)->a1, a(n + 2)->a3... 第i個元素去了第 ((2 * (i - n) ) - 1) = (2 * i - (2 * n + 1)) = (2 * i) % (2 * n + 1) 個位置。

統一一下，任意的第i個元素，我們最終換到了 (2 * i) % (2 * n + 1)的位置，這個取模很神奇，不會產生0。所有最終的位置編號還是從1到2n。

（1） 完美洗牌演算法1

於是，如果允許我們再用一個數組的話，我們直接把每個元素放到該放得位置就好了。於是產生了最簡單的方法pefect_shuffle1，它的時間複雜度是O(n)，空間複雜度也是O(n)。

程式碼：

1. // 時間O(n)，空間O(n) 陣列下標從1開始
2. void pefect_shuffle1(int *a,int n) {  
3. int n2 = n * 2, i, b[N];  
4.     for
    (i = 1; i <= n2; ++i) {  
5.         b[(i * 2) % (n2 + 1)] = a[i];  
6.     }  
7.     for (i = 1; i <= n2; ++i) {  
8.         a[i] = b[i];  
9.     }  
10. }  

（2） 完美洗牌演算法2——分治的力量。

考慮分治法，假設n也是偶數。 我們考慮把陣列拆成兩半：

       我們只寫陣列的下標：

原始陣列(1..2*n)

也就是(1..n)(n + 1.. 2 *n)

前半段長度為n，後半段長度也為n，我們把前半段的後n / 2個元素(n / 2 + 1..n)  與  後半段的前n / 2 個元素 (n + 1..n + n / 2 ) 交換，得到 :

新的前n個元素A ： (1..n / 2)(n + 1..n + n / 2 )

新的後n個元素B ： (n / 2 + 1.. n) (n + n / 2 + 1..n)

因為n是偶數,我們得到了A,B兩個子問題。問題轉化為了求解n' = n / 2的兩個問題。

當n是奇數怎麼辦？我們可以把前半段多出來的那個元素先拿出來，後面所有元素前移，再把當時多出的那個元素放到末尾，這樣數列最後兩個元素已經滿足要求了。於是只考慮前2 * (n - 1)個元素就可以了，於是轉換成了(n - 1)的問題。

為了說明問題，我們還是用a, b 分別說明一下。假設n = 4是個偶數，我們要做的數列是：

a1, a2,a3,a4,b1,b2,b3,b4

我們先要把前半段的後2個元素(a3,a4)與後半段的前2個元素(b1,b2)交換，得到a1,a2,b1,b2,a3,a4,b3,b4。

於是，我們分別求解子問題A (a1,a2,b1,b2)和子問題B (a3,a4,b3,b4)就可以了。

如果n = 5，是奇數數怎麼辦？

我們原始的陣列是a1,a2,a3,a4,a5,b1,b2,b3,b4,b5

我們先把a5拎出來，後面所有元素前移，再把a5放到最後，變為:

a1,a2,a3,a4,b1,b2,b3,b4,b5,a5

可見這時最後兩個元素b5,a5已經是我們要的結果了，所以我們只要考慮n=4就可以了。

那麼複雜度怎麼算？ 

每次，我們交換中間的n個元素，需要O(n)的時間，n是奇數的話，我們還需要O(n)的時間先把後兩個元素調整好，但這步影響總體時間複雜度。所以，無論如何都是O(n)的時間複雜度。

於是我們有 T(n) = T(n / 2) + O(n)  這個就是跟歸併排序一樣的複雜度式子，最終複雜度解出來T(n) = O(nlogn)。空間的話，我們就在陣列內部折騰的，所以是O(1)。（當然沒有考慮遞迴的棧的空間）

程式碼：

1. //時間O(nlogn) 空間O(1) 陣列下標從1開始
2. void perfect_shuffle2(int *a,int n) {  
3. int t,i;  
4.     if (n == 1) {  
5.         t = a[1];  
6.         a[1] = a[2];  
7.         a[2] = t;  
8.         return;  
9.     }  
10.     int n2 = n * 2, n3 = n / 2;  
11.     if (n % 2 == 1) {  //奇數的處理
12.         t = a[n];  
13.         for (i = n + 1; i <= n2; ++i) {  
14.             a[i - 1] = a[i];  
15.         }  
16.         a[n2] = t;  
17.         --n;  
18.     }  
19.     //到此n是偶數
20.     for (i = n3 + 1; i <= n; ++i) {  
21.         t = a[i];  
22.         a[i] = a[i + n3];  
23.         a[i + n3] = t;  
24.     }  
25.     // [1.. n /2]
26.     perfect_shuffle2(a, n3);  
27.     perfect_shuffle2(a + n, n3);  
28. }  

 這個演算法源自一篇文章，文章很數學，可以只記結論就好了……

這個演算法的具體實現還是依賴於演算法1，和演算法2的。

首先，對於每一個元素，它最終都會到達一個位置，我們如果記錄每個元素應到的位置會形成圈。

為什麼會形成圈？

比如原來位置為a的元素最終到達b，而b又要達到c……，因為每個新位置和原位置都有一個元素，所以一條鏈

a->b->c->d……這樣下去的話，必然有一個元素會指向a，（因為中間那些位置b,c,d……都已經被其它元素指向了）。

這就是圈的成因。

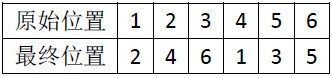
比如 6個元素 

原始是(1,2,3,4,5,6), 最終是(4,1,5,2,6,3),我們用a->b表示原來下標為a的元素，新下標為b了。

1->2

2->4

3->6

4->1

5->3

6->5

我們會發現1->2->4->1是個圈，3->6->5->3是另外一個圈。可以表示為(1,2,4) 和(3,6,5)，演算法1已經告訴我們每個位置i的元素，都變為2 * i % (2 * n + 1)，那麼我們只要知道圈裡的任意一個元素，順著走一遍就可以了，圈與圈是不相交的，所以這樣下來，我們就只走了O(n)步。

我們不能從1開始對每個元素都沿著圈走一圈。這是因為例如上例中(1,2,4)這個圈，我們只能從1，2， 4中的一個開始走一圈，而不能從1走一圈，再從2走一圈，再從4走一圈……因此我們可能還需要O(n)的空間記錄哪些元素所在的圈已經處理了，但是這樣做的時空複雜度等同於演算法1了。、（如果陣列元素都是正數，我們可以把處理過的元素標記為負數，最後再取相反數，但是這樣做其實也是利用了額外的空間的）。那麼我們的關鍵問題是從每個圈裡選擇任意一個位置作代表，每個圈從這個位置位置走一圈。而空間複雜度要求我們最好不要提前把每個代表位置存下來。後文一個定理表明，我們在陣列長度滿足一定條件情況下，每個圈中得最小元素可以簡單地表達出來。於是，我們稱每個圈的最小的位置叫做圈的頭部，用它來作圈的代表位置。如上例中圈(1,2,4)的頭部是1，(3,6,5)的頭部是3。如果我們知道了一個圈的頭部，用它做代表，沿著這個圈走就可以了。沿著圈走得算叫做cycle_leader,這部分程式碼如下：

1. //陣列下標從1開始，from是圈的頭部，mod是要取模的數 mod 應該為 2 * n + 1，時間複雜度O(圈長）
2. void cycle_leader(int *a,int from, int mod) {  
3. int last = a[from],t,i;  
4.     for (i = from * 2 % mod;i != from; i = i * 2 % mod) {  
5.         t = a[i];  
6.         a[i] = last;  
7.         last = t;  
8.     }  
9.     a[from] = last;  
10. }  

那麼如何找到每個圈的頭部呢？引用一篇論文，名字叫：

A Simple In-Place Algorithm for In-Shuffle.

Peiyush Jain, Microsoft Corporation.

利用數論知識，包括原根、甚至群論什麼的，論文給出了一個出色結論(*): 對於2 * n = (3^k - 1)，這種長度的陣列，恰好只有k個圈，並且每個圈的頭部是1,3,9,...3^(k - 1)。

這樣我們就解決了這種特殊的n作為長度的問題。那麼，對於任意的n怎麼辦？我們利用演算法2的思路，把它拆成兩部分，前一部分是滿足結論(*)。後一部分再單獨算。

為了把陣列分成適當的兩部分，我們同樣需要交換一些元素，但這時交換的元素個數不相等，不能簡單地迴圈交換，我們需要更強大的工具——迴圈移。

假設滿足結論(*)的需要的長度是2 * m = (3^k - 1)， 我們需要把n分解成m和n - m兩部分，按下標來說，是這樣：

原先的陣列(1..m) (m + 1.. n) (n + 1..n + m)(n + m + 1..2 * n)

我們要達到的陣列 (1..m)(n + 1.. n + m)(m + 1..n)(n + m + 1..2  * n)

可見，中間那兩段長度為(n - m)和m的段需要交換位置，這個相當於把(m + 1..n + m)的段迴圈右移m次，而迴圈右移是有O(長度)的演算法的, 主要思想是把前(n - m)個元素和後m個元素都翻轉一下，再把整個段翻轉一下。

迴圈移位的程式碼：

1. //翻轉字串時間複雜度O(to - from)
2. void reverse(int *a,int from,int to) {  
3. int t;  
4.     for (; from < to; ++from, --to) {  
5.         t = a[from];  
6.         a[from] = a[to];  
7.         a[to] = t;  
8.     }  
9. }  
10. //迴圈右移num位 時間複雜度O(n)
11. void right_rotate(int *a,int num,int n) {  
12.     reverse(a, 1, n - num);  
13.     reverse(a, n - num + 1,n);  
14.     reverse(a, 1, n);  
15. }  

再用a和b舉例一下，設n = 7這樣m = 4, k = 2

原先的陣列是a1,a2,a3,a4,(a5,a6,a7),(b1,b2,b3,b4),b5,b6,b7。

結論(*)是說m = 4的部分可以直接搞定，

也就是說我們把中間加括號的那兩段(a5,a6,a7) (b1,b2,b3,b4)交換位置，也就是把(a5,a6,a7,b1,b2,b3,b4)整體迴圈右移4位就可以得到：

(a1,a2,a3,a4,b1,b2,b3,b4)(a5,a6,a7,b5,b6,b7)

於是前m = 4個由演算法cycle_leading演算法直接搞定，n的長度減小了4。

所以這也是一種分治演算法。演算法流程：

輸入陣列　a[1..2 * n]

step 1 找到 2 * m = 3^k - 1 使得 3^k <= 2 * n < 3^(k +1)

step 2 把a[m + 1..n + m]那部分迴圈移m位

step 3 對每個i = 0,1,2..k - 1，3^i是個圈的頭部，做cycle_leader演算法，陣列長度為m，所以對2 * m + 1取模。

step 4 對陣列的後面部分a[2 * m + 1.. 2 * n]繼續使用本演算法, 這相當於n減小了m。

時間複雜度分析：

（1） 因為迴圈不斷乘3的，所以時間複雜度O(logn)

  (2)    迴圈移位O(n)

  (3)   每個圈，每個元素只走了一次，一共2*m個元素，所以複雜度omega(m), 而m < n，所以 也在O(n)內。

（4） T(n - m)

因此 複雜度為 T(n) = T(n - m) + O(n)      m = omega(n)  解得：總複雜度T(n) = O(n)。

演算法程式碼：

1. //時間O(n)，空間O(1)
2. void perfect_shuffle3(int *a,int n) {  
3. int n2, m, i, k,t;  
4.     for (;n > 1;) {  
5.         // step 1
6.         n2 = n * 2;  
7.         for (k = 0, m = 1; n2 / m >= 3; ++k, m *= 3)  
8.         ;  
9.         m /= 2;  
10.         // 2m = 3^k - 1 , 3^k <= 2n < 3^(k + 1)
11.         // step 2
12.         right_rotate(a + m, m, n);  
13.         // step 3
14.         for (i = 0, t = 1; i < k; ++i, t *= 3) {  
15.             cycle_leader(a , t, m * 2 + 1);  
16.         }  
17.         //step 4
18.         a += m * 2;  
19.         n -= m;  
20.     }  
21.     // n = 1
22.     t = a[1];  
23.     a[1] = a[2];  
24.     a[2] = t;  
25. }  

以上解決了完美洗牌問題，對於這個題，我們可以在完美洗牌之前把a的前n項與後n項交換掉,再呼叫perfect_shuffle3演算法。

程式碼：

1. //時間複雜度O(n)，空間複雜度O(1)，陣列下標從1開始，呼叫perfect_shuffle3
2. void shuffle(int *a,int n) {  
3.     int i,t;  
4.     for (i = 1; i <= n; ++i) {  
5.         t = a[i];  
6.         a[i] = a[i + n];  
7.         a[i + n] = t;  
8.     }  
9.     perfect_shuffle3(a,n);  
10. }  

程式碼：

1. //時間複雜度O(n)，空間複雜度O(1)，陣列下標從1開始，呼叫perfect_shuffle3
2. void shuffle(int *a,int n) {  
3.     int i,t,n2 = n * 2;  
4.     perfect_shuffle3(a,n);  
5.     for (i = 2; i <= n2; i += 2) {  
6.         t = a[i - 1];  
7.         a[i - 1] = a[i];  
8.         a[i] = t;  
9.     }  
10. }