主成份分析歷史：

Pearson於1901年提出，再由Hotelling（1933）加以發展的一種多變數統計方法。通過析取主成分顯出最大的個別差異，也用來削減迴歸分析和聚類分析中變數的數目，可以使用樣本協方差矩陣或相關係數矩陣作為出發點進行分析。

通過對原始變數進行線性組合，得到優化的指標：把原先多個指標的計算降維為少量幾個經過優化指標的計算（佔去絕大部分份額）

基本思想：設法將原先眾多具有一定相關性的指標，重新組合為一組新的互相獨立的綜合指標，並代替原先的指標。

成分的保留：Kaiser主張（1960）將特徵值小於1的成分放棄，只保留特徵值大於1的成分。

接下來以小學生基本生理屬性為案例分享下R語言的具體實現，分別選取身高（x1）、體重(x2)、胸圍(x3)和坐高(x4)。具體如下：

student<- data.frame(
			x1=c(148,139,160,149,159,142,153,150,151),
			x2=c(41 ,34 , 49 ,36 ,45 ,31 ,43 ,43, 42),
			x3=c(72 ,71 , 77 ,67 ,80 ,66 ,76 ,77,77),
			x4=c(78 ,76 , 86 ,79 ,86 ,76 ,83 ,79 ,80)
)
student.pr <- princomp(student,cor=TRUE)
summary(student.pr,loadings=TRUE)
screeplot(student.pr,type="lines")
 

結果如截圖：

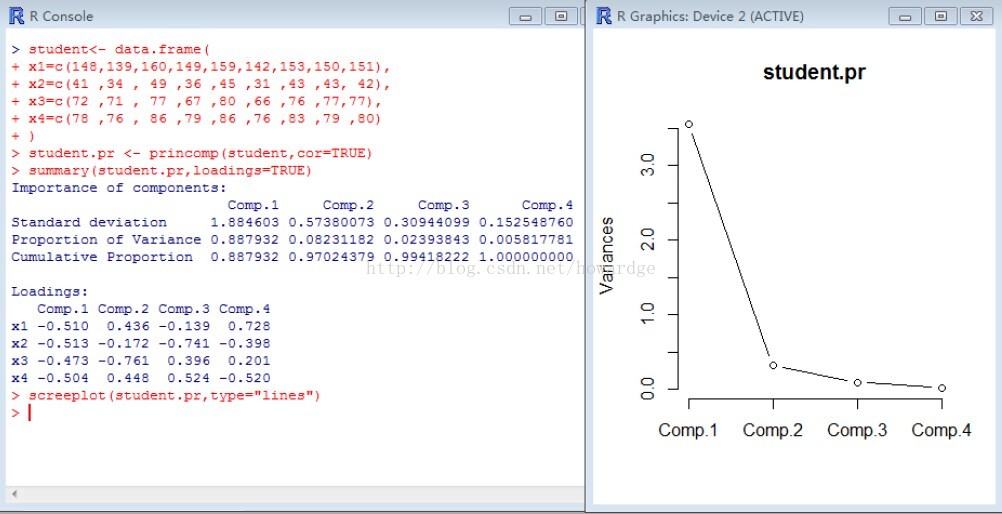
由上圖可見四項指標做分析後，給出了4個成分，他們的重要性分別為：0.887932、0.08231182、0.02393843、0.005817781，累積貢獻為：0.887932、0.97024379、

0.99418222 1.000000000各個成分的碎石圖也如上，可見成份1和成份2的累積貢獻已經達到95%，因此採用這兩個成份便可充分解釋學生的基本資訊。

我們可以通過R自動算出各主成份的值，並畫出散點圖：

temp<-predict(student.pr)
plot(temp[,1:2])

結果如圖：

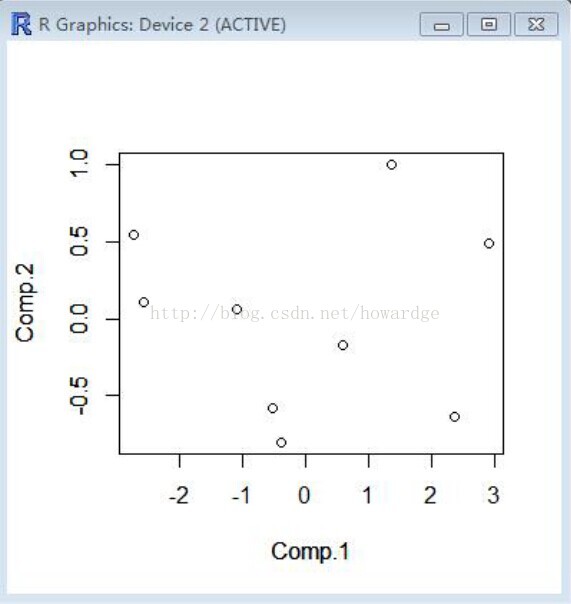
觀察如圖可見兩個成分的分離度很高，比較理想。