『Tarjan算法 有向圖的強連通分量』
<更新提示>
<第一次更新>
<正文>
有向圖的強連通分量
定義:在有向圖\(G\)中,如果兩個頂點\(v_i,v_j\)間\((v_i>v_j)\)有一條從\(v_i\)到\(v_j\)的有向路徑,同時還有一條從\(v_j\)到\(v_i\)的有向路徑,則稱兩個頂點強連通(\(strongly\ connected\))。如果有向圖\(G\)的每兩個頂點都強連通,稱\(G\)是一個強連通圖。有向圖的極大強連通子圖,稱為強連通分量(\(strongly\ connected\ components\))。
萬能的\(Tarjan\)算法也可以幫助我們求解有向圖的強聯通分量。
預備知識
時間戳
圖在深度優先遍歷的過程中,按照每一個節點第一次被訪問到的順序給\(N\)
追溯值
設節點\(x\)可以通過搜索樹以外的邊回到祖先,那麽它能回到祖先的最小時間戳稱為節點\(x\)的追溯值,記為\(low_x\)。當\(x\)沒有除搜索樹以外的邊時,\(low_x=x\)。
Tarjan 算法
著名的\(Tarjan\)算法可以在線性時間內求解有向圖的強聯通分量。
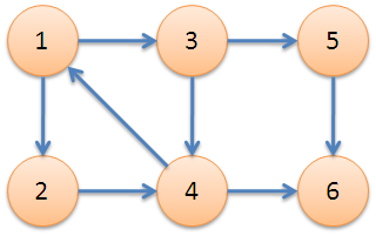
- 舉個栗子,右圖中,子圖\(\{1,2,3,4\}\)為一個強連通分量,因為頂點\(1,2,3,4\)兩兩可達。\(\{5\},\{6\}\)也分別是兩個強連通分量。
\(Tarjan\)求強連通分量的過程仍然是在遞歸求解\(dfn\)
\(Tarjan\)算法將每個強連通分量看作圖的搜索樹中的一棵子樹,搜索時,將每一個未回溯的節點加入一個棧,回溯時若\(dfn\)值與\(low\)值相等,則得到棧頂的若幹節點即為一個強連通分量。
我的理解:
回溯時若\(dfn\)值與\(low\)值相等,則說明以當前節點為根的子樹中的若幹節點都通過直接或間接路徑返回到了當前節點,而當前節點到那些節點顯然是可行的。也就是說,它們形成了若幹個環,構成了一個強連通分量。
實際上,\(low\)數組就是不斷在找"環"結構的過程。
其流程如下:
對於每一個當前訪問的點:
1.更新\(dfn\)和\(low\)的初始標記,\(low=dfn\)
2.遍歷當前節點的每一個子節點
3.如果其子節點未標記\(dfn\)值,訪問並更新,並順帶更新\(low\)值
4.如果已經訪問標記了\(dfn\)值,並且其子節點還在棧中,則該邊是一條返祖邊,更新\(low\)值
5.完成所有子節點的遍歷後,判斷\(dfn\)是否等於\(low\),若相等,則說明當前棧頂的若幹點(直到棧頂節點為當前節點)構成了一個強連通分量,記錄即可
\(Code:\)
inline void Tarjan(int x)
{
dfn[x]=low[x]=++cnt;
Stack.push(x);inSta[x]=true;
for(int i=Last[x];i;i=e[i].next)
{
int y=e[i].ver;
if(!dfn[y])
{
Tarjan(y);
low[x]=min(low[x],low[y]);
}
else if(inSta[y])low[x]=min(low[x],dfn[y]);
}
if(dfn[x]==low[x])
{
int top=0;tot++;
while(top!=x)
{
top=Stack.top();
Stack.pop();
inSta[top]=false;
con[top]=tot;
size[tot]++;
//這些點都在編號為tot的一個強連通分量中,con為查詢強連通分量的數組,size為強連通分量的大小
//儲存方式需要適時改變,以應合題目
}
}
}Tarjan算法的應用
通常,我們可以通過\(tarjan\)算法找到有向圖中的強連通分量,若將各個強連通分量壓縮成一個點,我們就得到了一個有向無環圖(\(DAG\)),這對我們的解題過程可以有所幫助。
最受歡迎的牛
Description
每頭牛都有一個夢想:成為一個群體中最受歡迎的名牛!
在一個有N(1<=N<=10,000)頭牛的牛群中,給你M(1<=M<=50,000)個二元組(A,B),表示A認為B是受歡迎的。
既然受歡迎是可傳遞的,那麽如果A認為B受歡迎,B又認為C受歡迎,則A也會認為C是受歡迎的,哪怕這不是十分明確的規定。你的任務是計算被所有其它的牛都喜歡的牛的個數。
Input Format
第一行,兩個數,N和M。
第2~M+1行,每行兩個數,A和B,表示A認為B是受歡迎的。
Output Format
一個數,被其他所有奶牛認為受歡迎的奶牛頭數。
Sample Input
3 3
1 2
2 1
2 3Sample Output
1解析
將牛的歡迎關系視為圖的連邊後,我們就得到了一張有向圖,不過不能保證無環。
我們放寬限制,假設給出的是有向無環圖,可以嘗試幾組樣例。
發現規律後我們可以得到猜想:若有且僅有一個點出度為0,則該點符合要求,答案總數為1,若有多於一個點出度為0,則沒有符合要求的點,答案總數為0。
那麽對於原圖,我們把每一個強連通分量壓縮為一個點,按有向無環圖的規律得到答案即可。若符合要求的點是一個由強連通分量壓縮得到的點,則答案數量為該強連通分量的大小。
這就成了一道強連通分量縮點模板題。
\(Code:\)
#include<bits/stdc++.h>
using namespace std;
const int N=20000+200,M=80000+200;
int n,m,dfn[N],low[N],cnt,Last[M*2],t,con[N],tot,inSta[N],outdeg[N],size[N],ans=0;
stack < int > Stack;
struct edge{int ver,next;}e[M*2];
inline void insert(int x,int y)
{
e[++t].ver=y;e[t].next=Last[x];Last[x]=t;
}
inline void input(void)
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int x,y;
scanf("%d%d",&x,&y);
insert(x,y);
}
}
inline void Tarjan(int x)
{
dfn[x]=low[x]=++cnt;
Stack.push(x);inSta[x]=true;
for(int i=Last[x];i;i=e[i].next)
{
int y=e[i].ver;
if(!dfn[y])
{
Tarjan(y);
low[x]=min(low[x],low[y]);
}
else if(inSta[y])low[x]=min(low[x],dfn[y]);
}
if(dfn[x]==low[x])
{
int top=0;tot++;
while(top!=x)
{
top=Stack.top();
Stack.pop();
inSta[top]=false;
con[top]=tot;
size[tot]++;
}
}
}
inline void build(void)
{
for(int i=1;i<=n;i++)
for(int j=Last[i];j;j=e[j].next)
if(con[i]^con[e[j].ver])outdeg[con[i]]++;
}
inline void find(void)
{
int flag=0;
for(int i=1;i<=tot;i++)
if(!outdeg[i])
{
if(!flag)flag=i;
else
{
ans=0;
return;
}
}
ans=size[flag];
}
int main(void)
{
input();
for(int i=1;i<=n;i++)
if(!dfn[i])Tarjan(i);
build();
find();
printf("%d\n",ans);
return 0;
}<後記>
對於\(Tarjan\)求強連通分量的理解,還可以參照這篇博客。
『Tarjan算法 有向圖的強連通分量』
