深度優先演算法和廣度優先演算法
今天做了道題目,《手機鍵盤輸入》當按下23時,輸出["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]。
其實說白了,也就是全排列問題,將2代表的abc,和3代表的def輸出組合的字元。
我是按照普通方法,遞迴來寫的,覺得這道題目也只是考驗程式設計,考驗遞迴的。沒太多考慮,當上網看別人都提到DFS(深度優先演算法)後,才意識到,是有章法可循的。以前只以為深度優先和廣度優先只是在圖的遍歷的時候才能用到,想不到這些也只是工具,看你怎麼去應用到你的演算法裡面。
好了,不多說了,基於上述原因,參考《資料結構》和《演算法導論》將廣度優先和深度優先總結一下。
這兩個演算法的共同點,都是要有標記!資料結構採用的是一個數組來標記每一個結點是否被遍歷;演算法導論是在結點中附設一個顏色值,來表示遍歷的程度。其實質是一樣的,都需要藉助於標記,來實現。但在二叉樹的遍歷中就不需要了,因為不會形成迴路。
一:深度優先演算法
方案一:“資料結構”
其實這是樹的先根遍歷的擴充套件。
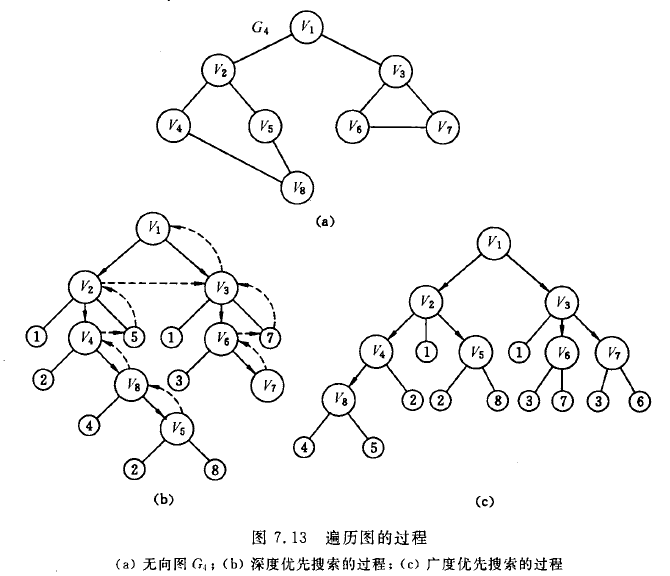
通過圖(b)我們可以看到,v1-v4-v8-v5-v3-v6-v7。
只要遍歷到某一個結點,有子節點就先遍歷子節點,當“子樹”遍歷完了以後,再遍歷另一個“子樹”,只是由於存在迴路,所以遍歷另一個子樹的時候,會訪問已經訪問過的點, 所以就需要標記來判斷。
程式碼如下:
Boolean visited[MAX]; //設定標誌陣列 Status (*VisitFunc)(int v); //全域性變數函式,方便在DFS中呼叫DFSTraverse中傳進的引數 void DFSTraverse(Graph G,Status (*Visit)(int v)) { VisitFunc = Visit; for(v = 0;v < G.vexnum;++v) //初始化,將標誌陣列全設為FALSE visited[v] = FALSE; for(v = 0;v < G.vexnum;++v) //對所有的結點進行遍歷,找到切入點,就呼叫DFS進行深度優先遍歷 if(!visited[v]) DFS(G,v); } void DFS(Graph G,int v) { visited[v] = TRUE; //給第v個結點標記,並訪問該結點。 VisitFunc(v); for(w = FirstAdjVex(G,v); w >= 0;w = NextAdjVex(G,v,w)) //對v的所有子節點w進行深度優先遍歷 if(!visited[w]) DFS(G,w); }
說明:
1:這個題目寫的很簡化,在visited[v]中v是一個確定的數值,表示陣列下標。但在VisitFunc(v)中,v為結點。雖然程式寫法簡化,但更能突出我們要解決的問題。
2:其實DFS和二叉樹的先序遍歷很相像:
visit(p);
PreOrderTraverse(p->left);
PreOrderTraverse(p->right);
其實就是將二叉樹的確定性,轉化成圖子節點的不確定性,通過for迴圈來實現。
3:DFS可以應用在樹的先序遍歷當中。
方案二:“演算法導論”
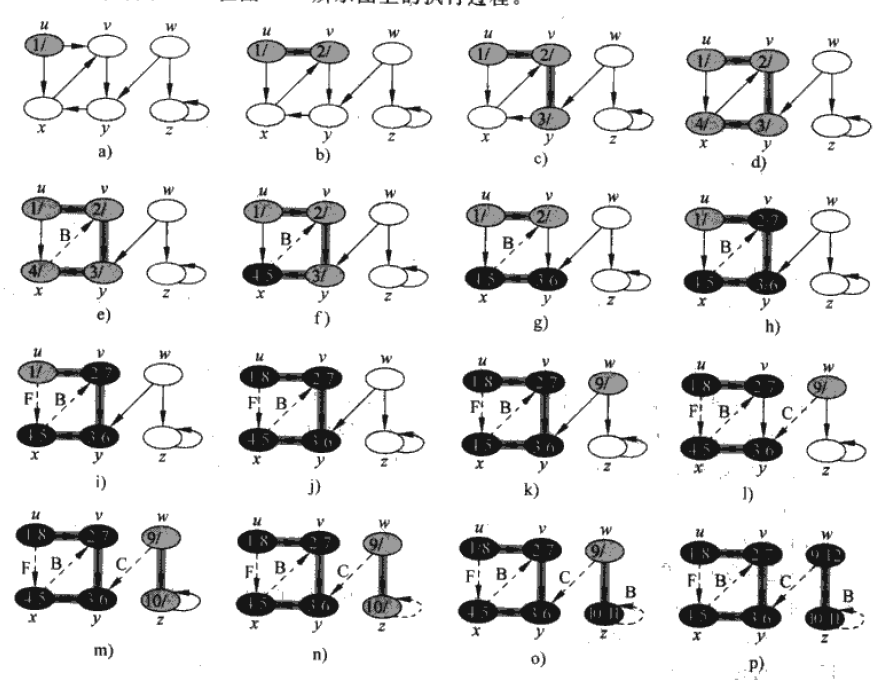
1:遍歷過程
只要可能,就在圖中儘量深入,總是對最近發現的結點v的出發邊進行探索,直到該結點的所有出發邊都被發現為止。然後回溯到v的父節點(可能有多個,但之前遍歷過程中,從哪個點過來的,就是v的父節點),然後搜尋該前驅結點的出發邊。知道從源節點可以達到的所有的出發邊都遍歷完。如果在圖中還有沒被遍歷的結點, 任選一個,重複上述過程。直到所有的結點遍歷完為止。
2:當發現一個結點v時,記錄其前驅結點u,並設定父節點指標v.π = u; 同樣設定三種顏色,白色表示尚未被遍歷的結點,灰色表示已經被遍歷,但其子節點還沒有被遍歷完全,黑色表示該結點以及所有的子節點都被遍歷完全,要返回到父節點。
3:給每個結點設定時間戳。v.d記錄第一次被發現的時間,v.f記錄對v掃描完成時的時間戳。其中time為全域性變數
程式碼:
DFS(G)
{
for(u = 0;u < G.vexnum;++u){ //初始化所有的結點資訊,父指標設為空,顏色全為白色
u.color = WHITE;
u.π = NULL;
}
time = 0;
for(u = 0;u < G.vexnum;++u) //開始遍歷所有的結點,以防存在多個不相接的圖
if(u.color == WHITE)
DFS_VISIT(G,u);
}
DFS_VISIT(G,u){
time = time + 1; //每次賦值前都要增加1,time為全域性變數
u.d = time;
u.color = GRAY; //當訪問了該結點,就將該節點設為灰色,接下來遍歷其子節點。其實不要該灰色指示也行
for(w = FirstAdjVex(G,v); w >= 0;w = NextAdjVex(G,v,w)) //處理子節點
if(w.color == WHITE){
w.π = u;
DFS_VISIT(G,w);
}
u.color = BLACK;
time = time + 1;
u.f = time;
}生成的圖
性質:
1、其生成的前驅製圖G形成一個由多棵樹所構成的森林,這是因為深度優先樹的結構與DFS_VISIT的遞迴呼叫結構完全對應。
2、結點的發現時間和完成時間具有括號化結構。也就是隻要兩個結點的時間有重疊,畢竟一個結點的時間段包含在另一個結點的時間段內。
二:廣度優先搜尋
類似於樹的按層次遍歷的過程。
方案一:“資料結構”
先訪問根結點,然後訪問與跟相連的所有結點v1-vn,然後訪問與v1-vn直接相連的所有結點(除去已經訪問過的結點)。這就要用佇列來時間:先訪問某結點,然後將該結點如佇列。從隊列出結點,然後依次訪問該結點的所有子節點(除去已經訪問過的結點),並將這些剛剛訪問結點入佇列(這樣將提前訪問過的結點就不用入隊列了,其子節點已經提前放入隊列當中)。
訪問過程是:v1-v2-v3-v4-v5-v6-v7-v8。
void BFSTraverse(Graph G,Status(*Visit)(int v))
{
for(u = 0;u < G.vexnum;++u) //初始化
visited[u] = FALSE;
InitQueue(Q);
for(v = 0;v < G.vexnum;++v){ //遍歷所有的結點
if(!visited[v]){
visited[v] = TRUE;
Visit(v); //先訪問再入佇列
EnQueue(Q,v);
while(!QueueEmpty(Q)){
DeQueue(Q,u);
for(w = FirstAdjVex(G,v); w >= 0;w = NextAdjVex(G,v,w)){
if(!visited[w]){
visited[w] = TRUE;
Visit(w);
EnQueue(Q,w);
}
}
}
}
}
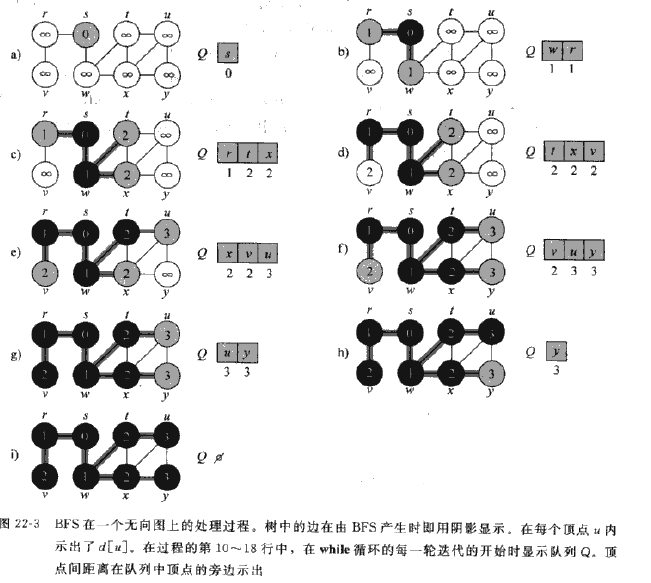
}方案二:“演算法導論”
該演算法可以得到最短路徑。
BFS(G,s)
{
for(u = 0;u < G.vexnum;++u){
u.color = WHITE;
u.d = 10000;
u.π = NULL;
}
s.color = GRAY;
s.d = 0;
s.π = NULL;
Q = 空
EnQueue(Q,s);
while(!IsEmpty(Q)){
u = DeQueue(Q);
for(w = FirstAdjVex(G,v); w >= 0;w = NextAdjVex(G,v,w)){
if(w.color == WHITE){
w.color = GRAY;
w.d = u.d + 1;
w.π = u;
EnQueue(Q,w);
}
}
u.color = BLACK;
}
}遍歷後的圖形:
因為我們有設定父節點指標,當通過廣度優先遍歷之後,我們從要找的葉節點反向遍歷到根結點,就能得到最短的路徑。
PRINT_PATH(G,s,v)
{
if(v == s)
print s;
else if(v.π == NULL){
print "no path form"s"to"v
}else{
PRINT_PATH(G,s,v.π)
print v;
}
}