C語言學習總結:浮點型在記憶體中的儲存
我們都知道,對於整形來說,資料存放記憶體中存放的是補碼。但是對於浮點型來說,在記憶體中存放的是否也是補碼呢?
舉個例子:
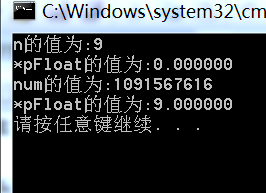
#define _CRT_SECURE_NO_WARNINGS 1 #include<stdio.h> int main() { int n = 9; float *pFloat = (float *)&n;//強制轉換型別 printf("n的值為:%d\n",n); printf("*pFloat的值為:%f\n",*pFloat); *pFloat = 9.0; printf("num的值為:%d\n",n); printf("*pFloat的值為:%f\n",*pFloat); return 0; }
num和*pFloat中存放的是同一個數,但是結果卻不一樣。所以,浮點型的儲存方式一定和整形是不一樣的。
那麼,浮點型資料是怎麼儲存的呢?
1.根據國際標準IEEE(電氣和電子工程協會)754,任意一個二進位制浮點數可以表示為下面的形式:
(-1)^S*M*2^E
a.(-1)^S表示符號位,當S=0時,表示正數,當S=1時,表示負數。
b.M表示有效數字,大於等於1,小於2。
c.2^E表示指數位。
例如:5.5寫成二進位制為101.1,相當於1.011*2^2,那麼,S=0,M=1.011,E=2。
2.IEEE 745規定:對於32位的浮點數,最高的1位是符號位S,接著的8位是指數E,剩下的23位為有效數字M。
單精度浮點數儲存模型
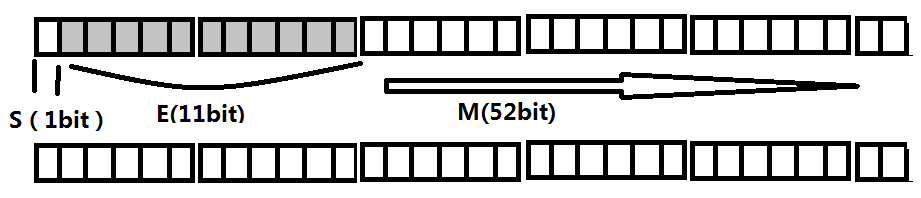
對於64位的浮點數,最高的1位是符號位S,接著的11位是指數E,剩下的52位為有效數字M。
雙精度浮點數儲存模型
3.IEEE 754對有效數字M和指數E,還有一些特別規定。
有效數字M:1<M<2,也就是說,M寫成1.xxxxxxx的形式,其中xxxxxxx表示小數部分。
IEEE 754規定,在計算機內部儲存M時,預設這個數的第一位總是1,因此可以被捨去,只儲存小數部分。比如儲存1.011時,只儲存011,後面的位數補0就可以了,等到讀取的時候,再把第一位的1補上去。
指數E:
首先,E為一個無符號整數(unsigned int)
如果E為8位,它的取值範圍為0~255;如果E為11位,它的取值範圍為0~2047。但是,我們知道,科學計數法是可以出現負數的,所以IEEE 754規定,存入記憶體的E是真實值加上一個中間數,對於8位的E,中間數是127,對於11位的E,中間數是1023。比如,2^2的E是2,所以儲存為32位浮點數時,必須儲存為2+127=129,即10000001。
然後,指數E還可以被分為三種情況:
E不全為0或不全為1
這個就是正常情況,取出記憶體中的數時,指數E的計算值減去127(或1023),得到真實值,再將有效數字M前加上第一位的1。
E全為0
這時,浮點數的指數E等於1-127(或1-1023)即為真實值,有效數字M不再加上第一位的1,而是還原為0.xxxxxxx的小數。這樣做是為了表示正負零,以及接近於0的很小的數字。
E全為1
這時,有效數字M全為0,表示正負無窮大。
好了,現在我們回到剛開始的例題,在第一部分中,整形數字9若還原成浮點數就變成了0,這是為什麼呢?
首先,將00000000000000000000000000001001拆分,第一位符號位S=0,後面8位的指數E=00000000,最後23位有效數字M=00000000000000000001001。由於指數E全為0,符合上述第二種情況,因此,浮點數是一個很小的接近於0的正數,所以用十進位制小數表示為0.000000。
在第二部分中,浮點數9.0用十進位制表示是一個很大的數。這又是為什麼呢?
首先,浮點數9.0等於二進位制的1001.0,即1.001*2^3。那麼,S=0,M=1.001,E=3+127=130。
就是這樣:0 10000010 00100000000000000000000
這個32位的二進位制數,還原成十進位制數,正是1091567616。