自編碼器（AutoEncoder）入門及TensorFlow實現

阿新 • • 發佈：2019-02-17

自編碼器（Autoencoder,AE）,是一種利用反向傳播演算法使得輸出值等於輸入值的神經網路，它先將輸入壓縮成潛在空間表徵，然後通過這種表徵來重構輸出。

自編碼器由兩部分組成：

編碼器（encoder）:這部分能將輸入壓縮成潛在空間表徵，可以用編碼函式h=f(x)表示。

解碼器（decoder）:這部分重構來自潛在空間表徵的輸入，可以用解碼函式r=g(h)表示。

因此，整個自編碼器可以用函式g(f(x)) = r 來描述，其中輸出r與原始輸入x相近。

一、為何要用輸入來重構輸出？

如果自編碼器的唯一目的是讓輸出值等於輸入值，那種人個演算法將毫無用處。事實上，我們希望通過訓練輸出值等於輸入值的自編碼器，讓潛在表徵h將具有價值屬性。

這可通過在重構任務中構建約束來實現。

從自編碼器獲得有用特徵的一種方法是，限制h的維度使其小於輸入x,這種情況下稱作有損自編碼器。通過訓練有損表徵，使得自編碼器能學習到資料中最重要的特徵。

如果潛在表徵的維度與輸入相同，或是在完備案例中潛在表徵的維度大於輸入，上述結果也會出現。

在這些情況下，即使只使用線性編碼器和線性解碼器，也能很好地利用輸入重構輸出，且無需瞭解有關資料分佈的任何有用資訊。

在理想情況下，根據要分配的資料複雜度，來準確選擇編碼器和解碼器的編碼維數和容量，就可以成功地訓練出任何所需的自編碼器結構。

二、自編碼器用來幹什麼？

目前，自編碼器的應用主要有兩個方面：

1.第一是資料去噪

2.第二是為

進行視覺化而降維。

設定合適的維度和稀疏約束，自編碼器可以學習到PCA等技術更有意思的資料投影。

自編碼器能從資料樣本中進行無監督學習，這意味著可以將這個演算法應用到某個資料集中，來取得良好的效能，且不需要任何新的特徵工程，只需要適當地訓練資料。

但是，自編碼器在影象壓縮方面表現的不好。由於在某個給定資料集上訓練自編碼器，因此它在處理與訓練集相類似的資料時可達到合理的壓縮結果，但是在壓縮差異較大的其他影象時效果不佳。這裡，像JPEG這樣的壓縮技術在通用影象壓縮方面會表現得更好。

訓練自編碼器，可以使輸入通過編碼器和解碼器後，保留儘可能多的資訊，但也可以訓練自編碼器來使新表徵具有多種不同的屬性。不同型別的自編碼器旨在實現不同型別的屬性。下面將重點介紹四中不同的自編碼器。

三、四種不同的自編碼器

本文將介紹以下四種不同的自編碼器：

香草自編碼器
多層自編碼器
卷積自編碼器
正則自編碼器

香草編碼器

在這種自編碼器的最簡單結構中，只有三個網路層，即只有一個隱藏層的神經網路。它的輸入和輸出是相同的，可通過使用Adam優化器和均方誤差損失函式，來學習如何重構輸入。

在這裡，如果隱含層維數（64）小於輸入維數（784），則稱這個編碼器是有損的。通過這個約束，來迫使神經網路來學習資料的壓縮表徵。

input_size = 784
hidden_size = 64
output_size = 784

x = Input(shape=(input_size,))

# Encoder
h = Dense(hidden_size, activation='relu')(x)

# Decoder
r = Dense(output_size, activation='sigmoid')(h)

autoencoder = Model(input=x, output=r)
autoencoder.compile(optimizer='adam', loss='mse')

多層自編碼器

如果一個隱含層還不夠，顯然可以將自動編碼器的隱含層數目進一步提高。

在這裡，實現中使用了3個隱含層，而不是隻有一個。任意一個隱含層都可以作為特徵表徵，但是為了使網路對稱，我們使用了最中間的網路層。

input_size = 784
hidden_size = 128
code_size = 64

x = Input(shape=(input_size,))

# Encoder
hidden_1 = Dense(hidden_size, activation='relu')(x)
h = Dense(code_size, activation='relu')(hidden_1)

# Decoder
hidden_2 = Dense(hidden_size, activation='relu')(h)
r = Dense(input_size, activation='sigmoid')(hidden_2)

autoencoder = Model(input=x, output=r)
autoencoder.compile(optimizer='adam', loss='mse')

卷積自編碼器

你可能有個疑問，除了全連線層，自編碼器應用到卷積層嗎？

答案是肯定的，原理是一樣的，但是要使用3D向量（如影象）而不是展平後的一維向量。對輸入影象進行下采樣，以提供較小維度的潛在表徵，來迫使自編碼器從壓縮後的資料進行學習。

x = Input(shape=(28, 28,1)) 

# Encoder
conv1_1 = Conv2D(16, (3, 3), activation='relu', padding='same')(x)
pool1 = MaxPooling2D((2, 2), padding='same')(conv1_1)
conv1_2 = Conv2D(8, (3, 3), activation='relu', padding='same')(pool1)
pool2 = MaxPooling2D((2, 2), padding='same')(conv1_2)
conv1_3 = Conv2D(8, (3, 3), activation='relu', padding='same')(pool2)
h = MaxPooling2D((2, 2), padding='same')(conv1_3)

# Decoder
conv2_1 = Conv2D(8, (3, 3), activation='relu', padding='same')(h)
up1 = UpSampling2D((2, 2))(conv2_1)
conv2_2 = Conv2D(8, (3, 3), activation='relu', padding='same')(up1)
up2 = UpSampling2D((2, 2))(conv2_2)
conv2_3 = Conv2D(16, (3, 3), activation='relu')(up2)
up3 = UpSampling2D((2, 2))(conv2_3)
r = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(up3)

autoencoder = Model(input=x, output=r)
autoencoder.compile(optimizer='adam', loss='mse')

正則自編碼器

除了施加一個比輸入維度小的隱含層，一些其他方法也可用來約束自編碼器重構，如正則自編碼器。

正則自編碼器不需要使用淺層的編碼器和解碼器以及小的編碼維數來限制模型容量，而是使用損失函式來鼓勵模型學習其他特性（除了將輸入複製到輸出）。這些特性包括稀疏表徵、小導數表徵、以及對噪聲或輸入缺失的魯棒性。

即使模型容量大到足以學習一個無意義的恆等函式，非線性且過完備的正則自編碼器仍然能夠從資料中學到一些關於資料分佈的有用資訊。

在實際應用中，常用到兩種正則自編碼器，分別是稀疏自編碼器和降噪自編碼器。

稀疏自編碼器：

一般用來學習特徵，以便用於像分類這樣的任務。稀疏正則化的自編碼器必須反映訓練資料集的獨特統計特徵，而不是簡單地充當恆等函式。以這種方式訓練，執行附帶稀疏懲罰的復現任務可以得到能學習有用特徵的模型。

還有一種用來約束自動編碼器重構的方法，是對其損失函式施加約束。比如，可對損失函式新增一個正則化約束，這樣能使自編碼器學習到資料的稀疏表徵。

要注意，在隱含層中，我們還加入了L1正則化，作為優化階段中損失函式的懲罰項。與香草自編碼器相比，這樣操作後的資料表徵更為稀疏。

input_size = 784
hidden_size = 64
output_size = 784

x = Input(shape=(input_size,))

# Encoder
h = Dense(hidden_size, activation='relu', activity_regularizer=regularizers.l1(10e-5))(x)#施加在輸出上的L1正則項

# Decoder
r = Dense(output_size, activation='sigmoid')(h)

autoencoder = Model(input=x, output=r)
autoencoder.compile(optimizer='adam', loss='mse')

降噪自編碼器：

這裡不是通過對損失函式施加懲罰項，而是通過改變損失函式的重構誤差項來學習一些有用資訊。

向訓練資料加入噪聲，並使自編碼器學會去除這種噪聲來獲得沒有被噪聲汙染過的真實輸入。因此，這就迫使編碼器學習提取最重要的特徵並學習輸入資料中更加魯棒的表徵，這也是它的泛化能力比一般編碼器強的原因。

這種結構可以通過梯度下降演算法來訓練。

x = Input(shape=(28, 28, 1))

# Encoder
conv1_1 = Conv2D(32, (3, 3), activation='relu', padding='same')(x)
pool1 = MaxPooling2D((2, 2), padding='same')(conv1_1)
conv1_2 = Conv2D(32, (3, 3), activation='relu', padding='same')(pool1)
h = MaxPooling2D((2, 2), padding='same')(conv1_2)

# Decoder
conv2_1 = Conv2D(32, (3, 3), activation='relu', padding='same')(h)
up1 = UpSampling2D((2, 2))(conv2_1)
conv2_2 = Conv2D(32, (3, 3), activation='relu', padding='same')(up1)
up2 = UpSampling2D((2, 2))(conv2_2)
r = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(up2)

autoencoder = Model(input=x, output=r)
autoencoder.compile(optimizer='adam', loss='mse')

使用tensorflow實現對手寫字(MNIST)的AutoEncoder

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

# Import MNIST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=False)


# Visualize decoder setting
# Parameters
learning_rate = 0.01
batch_size = 256
display_step = 1
examples_to_show = 10

# Network Parameters
n_input = 784  # 28x28 pix，即 784 Features

# tf Graph input (only pictures)
X = tf.placeholder("float", [None, n_input])

# hidden layer settings
n_hidden_1 = 256 # 經過第一個隱藏層壓縮至256個
n_hidden_2 = 128 # 經過第二個壓縮至128個
#兩個隱藏層的 weights 和 biases 的定義
weights = {
    'encoder_h1': tf.Variable(tf.random_normal([n_input, n_hidden_1])),
    'encoder_h2': tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2])),
    'decoder_h1': tf.Variable(tf.random_normal([n_hidden_2, n_hidden_1])),
    'decoder_h2': tf.Variable(tf.random_normal([n_hidden_1, n_input])),
}
biases = {
    'encoder_b1': tf.Variable(tf.random_normal([n_hidden_1])),
    'encoder_b2': tf.Variable(tf.random_normal([n_hidden_2])),
    'decoder_b1': tf.Variable(tf.random_normal([n_hidden_1])),
    'decoder_b2': tf.Variable(tf.random_normal([n_input])),
}

# Building the encoder
def encoder(x):
    # Encoder Hidden layer 使用的 Activation function 是 sigmoid #1
    layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, weights['encoder_h1']),
                                   biases['encoder_b1']))
    # Decoder Hidden layer with sigmoid activation #2
    layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, weights['encoder_h2']),
                                   biases['encoder_b2']))
    return layer_2


# Building the decoder
def decoder(x):
    # Encoder Hidden layer with sigmoid activation #1
    layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, weights['decoder_h1']),
                                   biases['decoder_b1']))
    # Decoder Hidden layer with sigmoid activation #2
    layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, weights['decoder_h2']),
                                   biases['decoder_b2']))
    return layer_2

'''

# Visualize encoder setting
# 只顯示解壓後的資料
learning_rate = 0.01    # 0.01 this learning rate will be better! Tested
training_epochs = 10
batch_size = 256
display_step = 1
# Network Parameters
n_input = 784  # MNIST data input (img shape: 28*28)
# tf Graph input (only pictures)
X = tf.placeholder("float", [None, n_input])
# hidden layer settings
n_hidden_1 = 128
n_hidden_2 = 64
n_hidden_3 = 10
n_hidden_4 = 2  #將原有784Features 的資料壓縮成2 Features資料
weights = {
    'encoder_h1': tf.Variable(tf.truncated_normal([n_input, n_hidden_1],)),
    'encoder_h2': tf.Variable(tf.truncated_normal([n_hidden_1, n_hidden_2],)),
    'encoder_h3': tf.Variable(tf.truncated_normal([n_hidden_2, n_hidden_3],)),
    'encoder_h4': tf.Variable(tf.truncated_normal([n_hidden_3, n_hidden_4],)),
    'decoder_h1': tf.Variable(tf.truncated_normal([n_hidden_4, n_hidden_3],)),
    'decoder_h2': tf.Variable(tf.truncated_normal([n_hidden_3, n_hidden_2],)),
    'decoder_h3': tf.Variable(tf.truncated_normal([n_hidden_2, n_hidden_1],)),
    'decoder_h4': tf.Variable(tf.truncated_normal([n_hidden_1, n_input],)),
}
biases = {
    'encoder_b1': tf.Variable(tf.random_normal([n_hidden_1])),
    'encoder_b2': tf.Variable(tf.random_normal([n_hidden_2])),
    'encoder_b3': tf.Variable(tf.random_normal([n_hidden_3])),
    'encoder_b4': tf.Variable(tf.random_normal([n_hidden_4])),
    'decoder_b1': tf.Variable(tf.random_normal([n_hidden_3])),
    'decoder_b2': tf.Variable(tf.random_normal([n_hidden_2])),
    'decoder_b3': tf.Variable(tf.random_normal([n_hidden_1])),
    'decoder_b4': tf.Variable(tf.random_normal([n_input])),#注意：在第四層時，輸出量不再是 [0,1] 範圍內的數，
    #而是將資料通過預設的 Linear activation function 調整為 (-∞,∞) 
}
def encoder(x):
    layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, weights['encoder_h1']),
                                   biases['encoder_b1']))
    layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, weights['encoder_h2']),
                                   biases['encoder_b2']))
    layer_3 = tf.nn.sigmoid(tf.add(tf.matmul(layer_2, weights['encoder_h3']),
                                   biases['encoder_b3']))
    layer_4 = tf.add(tf.matmul(layer_3, weights['encoder_h4']),
                                    biases['encoder_b4'])
    return layer_4
def decoder(x):
    layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, weights['decoder_h1']),
                                   biases['decoder_b1']))
    layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, weights['decoder_h2']),
                                   biases['decoder_b2']))
    layer_3 = tf.nn.sigmoid(tf.add(tf.matmul(layer_2, weights['decoder_h3']),
                                biases['decoder_b3']))
    layer_4 = tf.nn.sigmoid(tf.add(tf.matmul(layer_3, weights['decoder_h4']),
                                biases['decoder_b4']))
    return layer_4
'''

# Construct model
encoder_op = encoder(X)
decoder_op = decoder(encoder_op)

# Prediction
y_pred = decoder_op
# Targets (Labels) are the input data.
y_true = X

# Define loss and optimizer, minimize the squared error
#比較原始資料與還原後的擁有 784 Features 的資料進行 cost 的對比，
#根據 cost 來提升我的 Autoencoder 的準確率
loss = tf.reduce_mean(tf.pow(y_true - y_pred, 2))#進行最小二乘法的計算(y_true - y_pred)^2
#loss = tf.reduce_mean(tf.square(y_true - y_pred))
optimizer = tf.train.AdamOptimizer(learning_rate).minimize(loss)


# Launch the graph
with tf.Session() as sess:
    init = tf.global_variables_initializer()
    sess.run(init)
    total_batch = int(mnist.train.num_examples/batch_size)
    training_epochs = 20
    # Training cycle
    for epoch in range(training_epochs):#到好的的效果，我們應進行10 ~ 20個 Epoch 的訓練
        # Loop over all batches
        for i in range(total_batch):
            batch_xs, batch_ys = mnist.train.next_batch(batch_size)  # max(x) = 1, min(x) = 0
            # Run optimization op (backprop) and cost op (to get loss value)
            _, c = sess.run([optimizer, loss], feed_dict={X: batch_xs})
        # Display logs per epoch step
        if epoch % display_step == 0:
            print("Epoch:", '%04d' % (epoch+1),
                  "cost=", "{:.9f}".format(c))
    print("Optimization Finished!")

    # Applying encode and decode over test set
    encode_decode = sess.run(
        y_pred, feed_dict={X: mnist.test.images[:examples_to_show]})
    # Compare original images with their reconstructions
    f, a = plt.subplots(2, 10, figsize=(10, 2))
    for i in range(examples_to_show):
        a[0][i].imshow(np.reshape(mnist.test.images[i], (28, 28)))
        a[1][i].imshow(np.reshape(encode_decode[i], (28, 28)))

    plt.show()

    # encoder_result = sess.run(encoder_op, feed_dict={X: mnist.test.images})
    # sc = plt.scatter(encoder_result[:, 0], encoder_result[:, 1], c=mnist.test.labels) #散點圖
    # plt.colorbar(sc) #scatter設定顏色漸變條colorbar
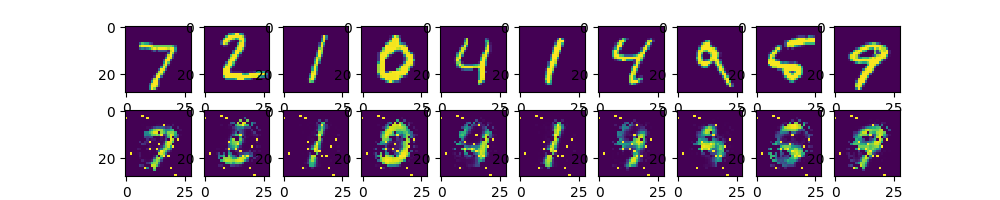
    # plt.show()

上面一行圖片為測試圖片，第二行為經過自編碼器後輸出

圖1 手寫數字照片經自編碼器輸出與原照片對比

應用--基於降噪自編碼器的情感分析

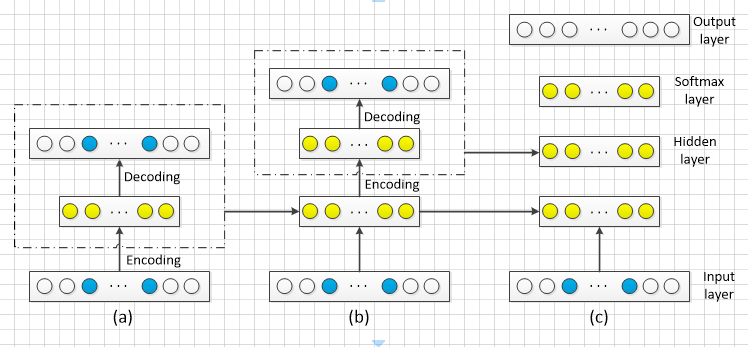
一個簡單的降噪自動編碼器如圖2( a) 所示，最底層的小圓代表原始資料而帶淡藍色的小圓則是噪聲資料。將這些資料輸入到編碼器中會得到輸入資料的一個表示，再將這個表示通過解碼器輸出一個資訊，通過調整編碼器和解碼器的引數使得重構誤差最小。

將上一層的輸出作為下一層的輸入，其逐層嵌入可如圖2( b) 所示。為了實現情感分析的任務，必須在輸出層的前一層新增一個分類器softmax 層，然後通過標準的多層神經網路監督訓練梯度下降法，最後得到如圖2( c) 中的堆疊多隱層的降噪自動編碼器。

圖2 降噪自動編碼器的逐層嵌入與訓練模型

總結

本文先介紹了自編碼器的基本結構，還研究了許多不同型別的自編碼器，如香草、多層、卷積和正則化，通過施加不同的約束，包括縮小隱含層的維度加入懲罰項，使得每種自編碼器具有不同屬性。

希望這篇文章能讓深度學習初學者對自編碼器有個很好的認識。

自編碼器（AutoEncoder）入門及TensorFlow實現

一、為何要用輸入來重構輸出？

二、自編碼器用來幹什麼？

三、四種不同的自編碼器

香草編碼器

多層自編碼器

卷積自編碼器

正則自編碼器

稀疏自編碼器：

降噪自編碼器：

使用tensorflow實現對手寫字(MNIST)的AutoEncoder

圖1 手寫數字照片經自編碼器輸出與原照片對比

應用--基於降噪自編碼器的情感分析

圖2 降噪自動編碼器的逐層嵌入與訓練模型

總結

自編碼器（AutoEncoder）入門及TensorFlow實現

深度學習：什麼是自編碼器（Autoencoder）

從零上手變分自編碼器（VAE）

深度學習筆記：稀疏自編碼器（1）——神經元與神經網路

自動編碼器（Autoencoder）keras實現---轉載

【Learning Notes】變分自編碼器（Variational Auto-Encoder，VAE）

Android視音頻編碼器（2）——cameraYUV、AudioRecordPCM分別編碼後muxer成mp4

變分貝葉斯自編碼器（VAE) 匯總

生成模型--稀疏自編碼器(sparse autoencoder，SAE)

生成模型--降噪自編碼器(denoising autoencoder，DAE)

Spring Boot 官方文件學習（一）入門及使用

JAVA過濾器（Filter）與攔截器（Interceptor）區別及關係

分享基於.NET動態編譯&Newtonsoft.Json封裝實現JSON轉換器（JsonConverter）原理及JSON操作技巧

Pytest學習（一）- 入門及基礎

Linux時間子系統之六：高精度定時器（HRTIMER）的原理和實現

（轉）sslvpn及openvpn實現原理

開放分散式追蹤（OpenTracing）入門與 Jaeger 實現

粒子群優化演算法（PSO）簡介及MATLAB實現

自定義堆（2）：通過堆實現優先佇列

TensorFlow 從入門到精通（五）：使用 TensorFlow 實現 RNN

自編碼器（AutoEncoder）入門及TensorFlow實現

一、為何要用輸入來重構輸出？

二、自編碼器用來幹什麼？

三、四種不同的自編碼器

香草編碼器

多層自編碼器

卷積自編碼器

正則自編碼器

稀疏自編碼器：

降噪自編碼器：

使用tensorflow實現對手寫字(MNIST)的AutoEncoder

圖1 手寫數字照片經自編碼器輸出與原照片對比

應用--基於降噪自編碼器的情感分析

圖2 降噪自動編碼器的逐層嵌入與訓練模型

總結

相關推薦