已知一段圓弧的起點、終點、弧度和法向，求此段圓弧的引數方程和引數區間。

P(U) = O + R*Cos(U)*XDir + R*Sin(U)*YDir

        這個問題主要應用於二維多段線中圓弧段的求解。在這裡我先講一下二維多段線的構造。

二維多段線

        二維多段線由直線段和圓弧段構成，二維的意思是多段線是固定在某一個平面上的，這個平面可由使用者任意指定。在ObjectARX中把這個平面稱作OCS(object coordinate system, 物件座標系)，兩個引數可以確定這個OCS：平面的法向normal，WCS(world coordinate system, 世界座標系)的原點到OCS的原點的距離，求法可參見

object coordinate systems，根據座標系統構造轉換矩陣（不包含縮放）。         下面來仔細說一下ObjectARX中二維多段線的引數。
        二維多段線的引數有：P1（第1點座標），...，Pn（第n點座標）；Bulge_1，...，Bulge_n。其中Bulge_n是指第n點是圓弧的起點時，Bulge_n=tan(α/4)，其中α是圓弧的夾角（從起點到終點，右手座標系），如果第n點是直線的起點時，Bulge_n=0。         為什麼Bulge_n=tan(α/4)？因為三角函式tan(α)的一個週期是[-π/2, π/2]，而因為圓弧的 角度區間為[-2π, 2π]，取Bulge_n=tan(α/4)，是將圓弧的角度壓縮到[-π/2, π/2]，這樣可以逆向求得α。

問題求解

        如下圖所示問題的俯檢視和側檢視：

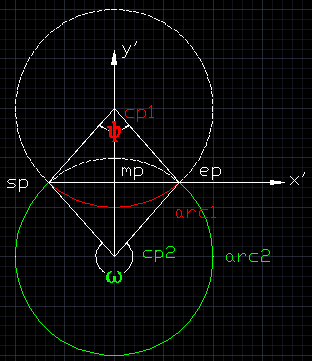
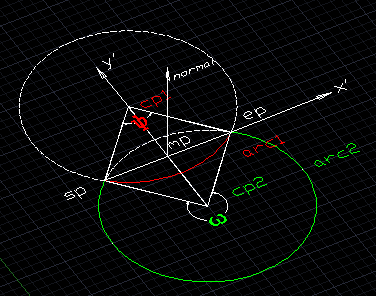
如上圖所示，點sp和ep分別為圓弧的起點和終點，點mp為線段spep的中點，法向normal朝向螢幕外，x'軸向為epsp方向，y‘軸向為以點mp為起點，normal×x'方向。當弧度θ為ω＞π時，圓弧為arc2，點cp2為此圓弧的圓心；當弧度θ為0＜ψ＜π時，圓弧為arc1，點cp1為此圓弧的圓心。（ps: 圓弧的走勢始終是以sp為起點，逆時針繞至終點ep。基於此，若給定的弧度θ＜0，則取絕對值|θ|，並將normal反向。）         下面列出求解過程的虛擬碼（假設給定的弧度θ＞0）。

mp = (sp+ep)/2；
y’ = normalize(normal×spep)；
cp = mp + y’|spmp|cotθ/2；
radius = |spmp|/sinθ/2；
xAxis = normalize(cpsp)；
yAxis = normalize(normal×xAxis)。
區間為[0, θ]。