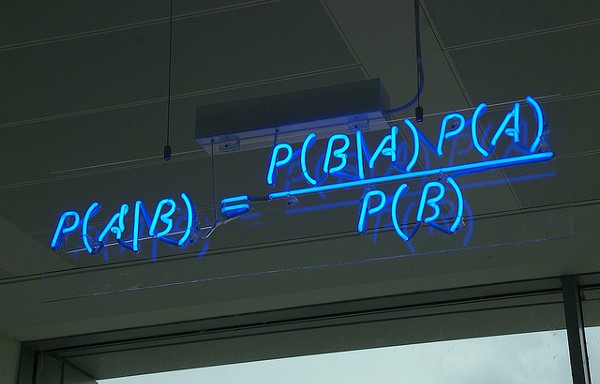機器學習應該瞭解的十大演算法
毫無疑問,近些年機器學習和人工智慧領域受到了越來越多的關注。隨著大資料成為當下工業界最火爆的技術趨勢,機器學習也藉助大資料在預測和推薦方面取得了驚人的成績。比較有名的機器學習案例包括Netflix根據使用者歷史瀏覽行為給使用者推薦電影,亞馬遜基於使用者的歷史購買行為來推薦圖書。
那麼,如果你想要學習機器學習的演算法,該如何入門呢?就我而言,我的入門課程是在哥本哈根留學時選修的人工智慧課程。老師是丹麥科技大學應用數學和計算機專業的全職教授,他的研究方向是邏輯學和人工智慧,主要是用邏輯學的方法來建模。課程包括了理論/核心概念的探討和動手實踐兩個部分。我們使用的教材是人工智慧的經典書籍之一:Peter Norvig教授的《人工智慧——一種現代方法》
我從課程中學到了非常多的知識,並且打算在這個專題裡繼續深入學習。在過去幾周內,我參與了舊金山地區的多場深度學習、神經網路和資料架構的演講 —— 還有一場眾多知名教授雲集的機器學習會議。最重要的是,我在六月初註冊了Udacity的《機器學習導論》線上課程,並且在幾天前學完了課程內容。在本文中,我想分享幾個我從課程中學到的常用機器學習演算法。
機器學習演算法通常可以被分為三大類 —— 監督式學習,非監督式學習和強化學習。監督式學習
監督式學習
1.決策樹:
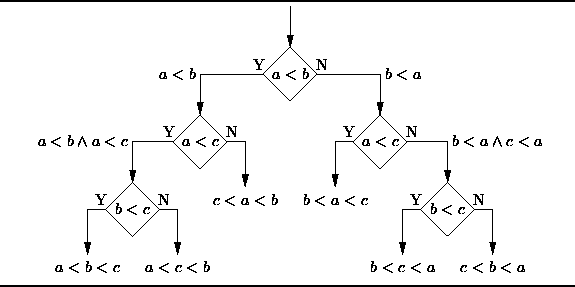
決策樹是一種決策支援工具,它使用樹狀圖或者樹狀模型來表示決策過程以及後續得到的結果,包括概率事件結果等。請觀察下圖來理解決策樹的結構。
從商業決策的角度來看,決策樹就是通過儘可能少的是非判斷問題來預測決策正確的概率。這種方法可以幫你用一種結構性的、系統性的方法來得出合理的結論。
2.樸素貝葉斯分類器:
樸素貝葉斯分類器是一類基於貝葉斯理論的簡單的概率分類器,它假設特徵之前是相互獨立的。下圖所示的就是公式 —— P(A|B)表示後驗概率,P(B|A)是似然值,P(A)是類別的先驗概率,P(B)代表預測器的先驗概率。
現實場景中的一些例子包括:
- 檢測垃圾電子郵件
- 將新聞分為科技、政治、體育等類別
- 判斷一段文字表達積極的情緒還是消極的情緒
- 用於人臉檢測軟體
3.最小平方迴歸:
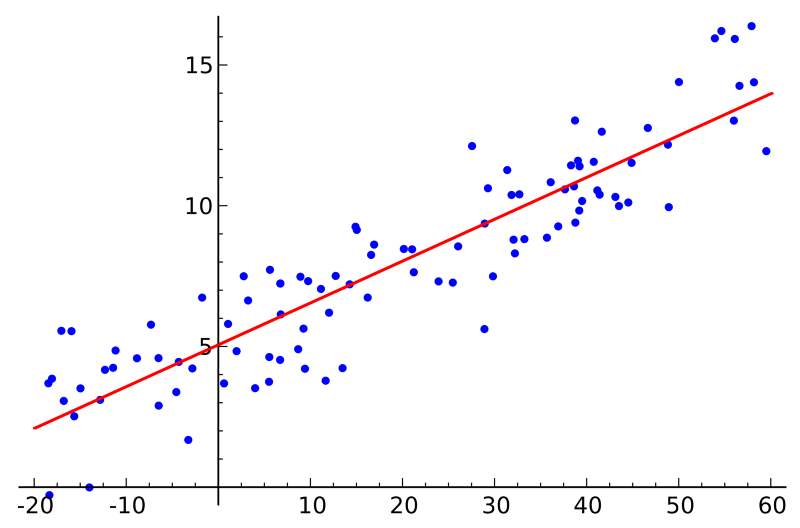
如果你學過統計課程,也許聽說過線性迴歸的概念。最小平方迴歸是求線性迴歸的一種方法。你可以把線性迴歸想成是用一條直線擬合若干個點。擬合的方法有許多種,“最小平方”的策略相當於你畫一條直線,然後計算每個點到直線的垂直距離,最後把各個距離求和;最佳擬合的直線就是距離和最小的那一條。
線性指的是用於擬合數據的模型,而最小平方指的是待優化的損失函式。
4.邏輯迴歸:
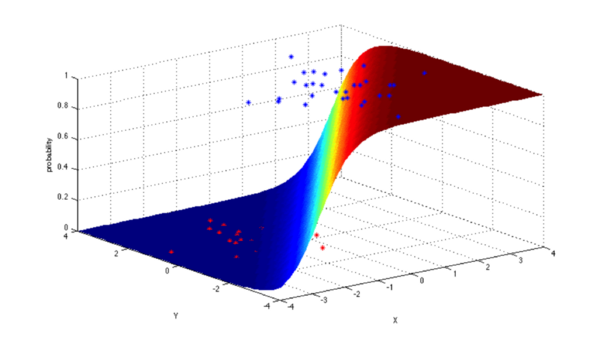
邏輯迴歸模型是一種強大的統計建模方式,它用一個或多個解釋性變數對二值輸出結果建模。它用邏輯斯蒂函式估計概率值,以此衡量分類依賴變數和一個或多個獨立的變數之間的關係,這屬於累積的邏輯斯蒂分佈。
通常來說,邏輯迴歸模型在現實場景中的應用包括:
- 信用評分
- 預測商業活動的成功概率
- 預測某款產品的收益
- 預測某一天發生地震的概率
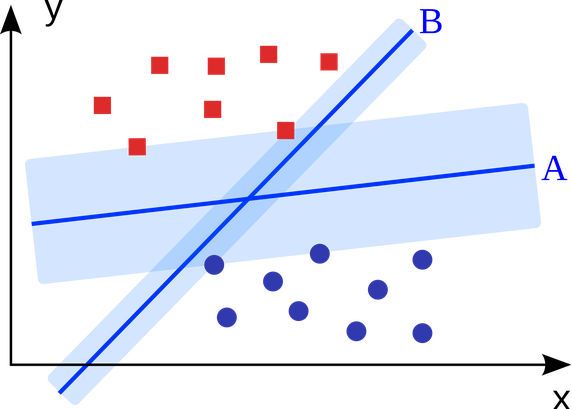
5.支援向量機:
支援向量機是一種二分類演算法。在N維空間中給定兩類點,支援向量機生成一個(N-1)維的超平面將這些點分為兩類。舉個例子,比如在紙上有兩類線性可分的點。支援向量機會尋找一條直線將這兩類點區分開來,並且與這些點的距離都儘可能遠。
利用支援向量機(結合具體應用場景做了改進)解決的大規模問題包括展示廣告、人體結合部位識別、基於影象的性別檢查、大規模影象分類等……
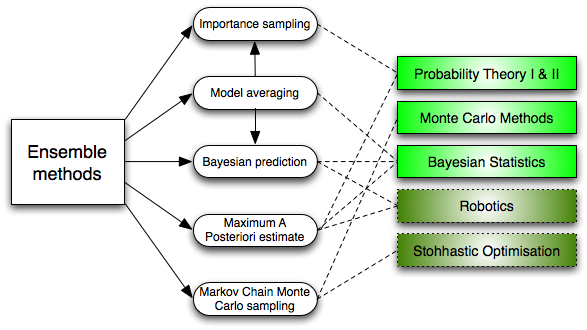
6.整合方法:
整合方法是先構建一組分類器,然後用各個分類器帶權重的投票來預測新資料的演算法。最初的整合方法是貝葉斯平均,但最新的演算法包括誤差糾正輸出編碼和提升演算法。
那麼整合模型的原理是什麼,以及它為什麼比獨立模型的效果好呢?
- 它們消除了偏置的影響:比如把民主黨的問卷和共和黨的問卷混合,從中得到的將是一個不倫不類的偏中立的資訊。
- 它們能減小預測的方差:多個模型聚合後的預測結果比單一模型的預測結果更穩定。在金融界,這被稱為是多樣化 —— 多個股票的混合產品波動總是遠小於單個股票的波動。這也解釋了為何增加訓練資料,模型的效果會變得更好。
- 它們不容易產生過擬合:如果單個模型不會產生過擬合,那麼將每個模型的預測結果簡單地組合(取均值、加權平均、邏輯迴歸),沒有理由產生過擬合。
非監督學習
7.聚類演算法:
聚類演算法的任務是將一群物體聚成多個組,分到同一個組(簇)的物體比其它組的物體更相似。
每種聚類演算法都各不相同,這裡列舉了幾種:
- 基於類心的聚類演算法
- 基於連線的聚類演算法
- 基於密度的聚類演算法
- 概率型演算法
- 降維演算法
- 神經網路/深度學習
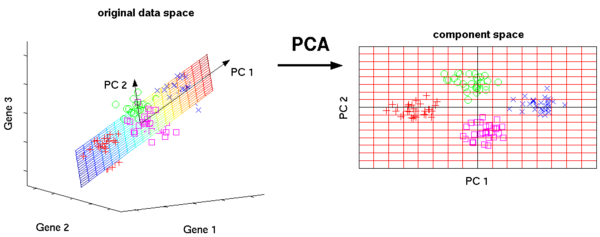
8.主成分分析:
主成分分析屬於統計學的方法,過正交變換將一組可能存在相關性的變數轉換為一組線性不相關的變數,轉換後的這組變數叫主成分。
主成分分析的一些實際應用包括資料壓縮,簡化資料表示,資料視覺化等。值得一提的是需要領域知識來判斷是否適合使用主成分分析演算法。如果資料的噪聲太大(即各個成分的方差都很大),就不適合使用主成分分析演算法。
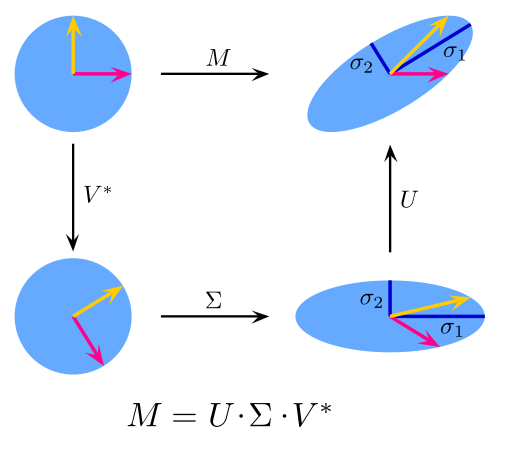
9.奇異值分解:
奇異值分解是線性代數中一種重要的矩陣分解,是矩陣分析中正規矩陣酉對角化的推廣。對於給定的m*n矩陣M,可以將其分解為M = UΣV,其中U和V是m×m階酉矩陣,Σ是半正定m×n階對角矩陣。
主成分分析其實就是一種簡單的奇異值分解演算法。在計算機視覺領域中,第一例人臉識別演算法使用了主成分分析和奇異值分解將人臉表示為一組“特徵臉(eigenfaces)”的線性組合,經過降維,然後利用簡單的方法匹配候選人臉。儘管現代的方法更加精細,許多技術還是於此很相似。
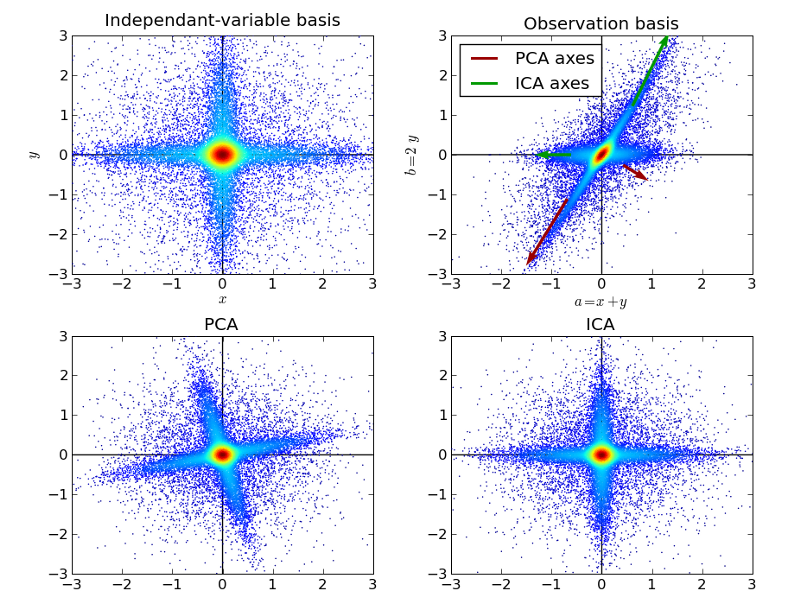
10.獨立成分分析:
獨立成分分析是一種利用統計原理進行計算來揭示隨機變數、測量值或者訊號背後的隱藏因素的方法。獨立成分分析演算法給所觀察到的多變數資料定義了一個生成模型,通常這些變數是大批量的樣本。在該模型中,資料變數被假定為一些未知的潛變數的線性混合,而且混合系統也未知。潛變數被假定是非高斯和相互獨立的,它們被稱為所觀察到的資料的獨立分量。
獨立成分分析與主成分分析有關聯,但它是一個更強大的技術。它能夠在這些經典方法失效時仍舊找到資料來源的潛在因素。它的應用包括數字影象、文件資料庫、經濟指標和心理測量。
現在,請運用你所理解的演算法,去創造機器學習應用,改善全世界人們的生活質量吧。