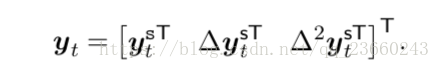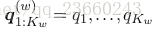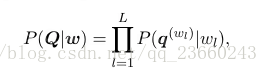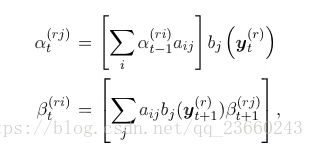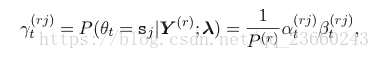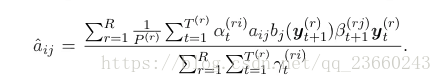基於HMM的語音識別(二)
今天進入特徵提取部分,原文的2.1部分,進入正題。
特徵提取階段試圖提供語音波形的緊湊形式(這裡我理解不是很好,往下看)。這種形式最大限度的減少單詞間的區分資訊的丟失,並且與聲學模型的分佈假設進行良好的匹配。比如,如果對角協方差高斯分佈用於狀態輸出分佈,那麼這些特徵應該被設計為高斯並且是不相關的。
通常使用約25ms的重疊分析窗每10ms計算一次特徵向量。其中最簡單也是最常用的編碼方式是梅爾倒譜系數也就是大名鼎鼎的MFCC。這些是利用截斷離散餘弦變換生成一個對數譜估計,該對數譜是利用平滑一個大約20個頻段非線性分佈的語譜的傅立葉變換得到的。非線性的頻率範圍通常被稱之為梅爾範圍(mel scale),他很逼近人耳的響應。DCT之所以被利用是為了平滑譜估計並且對特徵元素去相關。經過餘弦變換,第一個元素表示頻帶的對數能量平均值。這有時會被幀的對數能量所取代,或者完全刪除。
進一步的約束被嵌入到感知線性預測(PLP)中。PLP根據感知加權的非線性壓縮功率譜來計算線性預測係數,然後將線性預測係數轉換為倒譜系數。PLP根據感知加權的非線性壓縮功率來計算線性預測係數,然後將線性預測係數轉換為倒譜系數。在實際應用中,PLP比MFCC在嘈雜的環境裡有更好的表現,所以PLP一般是更好的編碼方式。
除了倒譜系數以外,一階和二階迴歸係數通常也被新增到啟發式的嘗試中,以補償由基於HMM的聲學模型產生的條件獨立性假設。如果原始的特徵向量為yt^s,那麼delta引數為:
其中n是視窗長度,wi是迴歸係數。delta-delta係數同理,當我們把上述放在一起時候如下:
最後的結果是一個大約40維度的特徵向量,他們平行但是不是完全相互獨立。
【PS:這段其實說的並不是很仔細,或者很清楚,因為MFCC其實是一個大的專題,並不是這一兩句能說清楚的,我日後如果有機會會做一篇MFCC的文章,並且把程式寫出來放到git,這裡暫且先這麼認為,我們在梳理】
HMM聲學模型
正如我們前面所說的,我們說的每個單詞wk都可以分解為Kw個基本因素的序列。這個序列我們稱之為發音:
為了適應多重發音的這種情況,我們可以通過多重發音來計算相似度p(Y|w):
這裡的求和是對w所有可能的發音的序列求解的,Q是特定發音的序列:
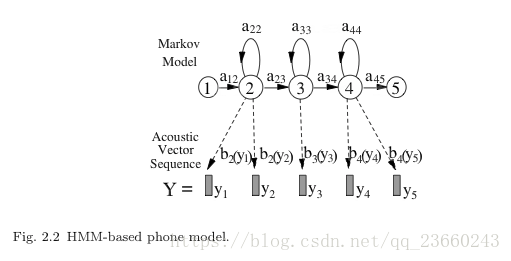
但是事實上,wl的不同發音僅很少個數,對於上述式子的追蹤還是很容易的。每一個因素q都被一個連續密度的HMM模型所描述,如下:
aij表示轉移概率,bj()表示輸出的觀測分佈。在執行的時候,一個HMM模型在每個時間步長上使得從一個狀態轉移到另一個狀態,那麼這個特殊的從si到sj狀態轉移的概率就是aij。進入一個狀態後,通過進入狀態的概率分佈得到特徵向量,而這個分佈就是bj()。這種處理的形式產生標準的條件不相關的假設:
1. 在知道前一個狀態的前提下,本狀態和其他狀態都是相互條件獨立的。
2. 在給定生成觀測序列的狀態的前提下,觀測序列都是條件獨立的。
目前為止,單多變數高斯模型的分佈假設如下:
其中u是狀態sj的均值,累加符號是他的協方差。由於聲音向量y的維數相當大,我們的協方差經常約定為對角的。在後面的HMM Structure Refinements,我們將會討論混合高斯模型的好處。
給定我們的合成物Q同時把所有的基礎音素串聯,我們可以得到聲音相似度如下:
其中sita是狀態的序列,展開後者:
其中sita0和sitaT+1表示輸入和輸出狀態。
聲音模型的引數:
本引數可以通過使用前後向演算法在訓練資料上高效的被估計出來,比如期望最大。對於每個語音來說Y^r,r=1....R,在語音中對應詞序列的HMM被找到,並且綜合HMM被構建。在演算法的第一階段,E-step,前向概率為: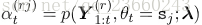
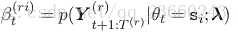
對於長語音上面的式子可能會發生下溢,所以改成log概率去避免這個問題。
在給定前向和後向概率的情況下,在t時刻給定語音r的模型狀態在sj的概率為:
其中
他們是通過給出前面對齊的情況下最大化相似度來得到的。一個相似的重估方程為轉移概率誕生:
這是演算法的第二或者第M步。從一些初始化的引數開始,
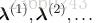
這種聲學建模的方式通常稱之為 beads-on-a-string(表面譯為串成一串的珠子),之所以這麼叫是因為語音發音完全被音素模型的序列串聯表示。這種方式最大的缺點在於把每個詞彙分解成上下文獨立的基本音素很難捕獲那些在實際語音中上下文相關的變數。打個比方,mood和cool兩個詞語的基本發音都是相同的母音“oo”,然而在實際中,由於oo前後的環境不同,其實現可能是非常不同的。我們叫上下文獨立的音素模型為monophones,也就是單因素模型。
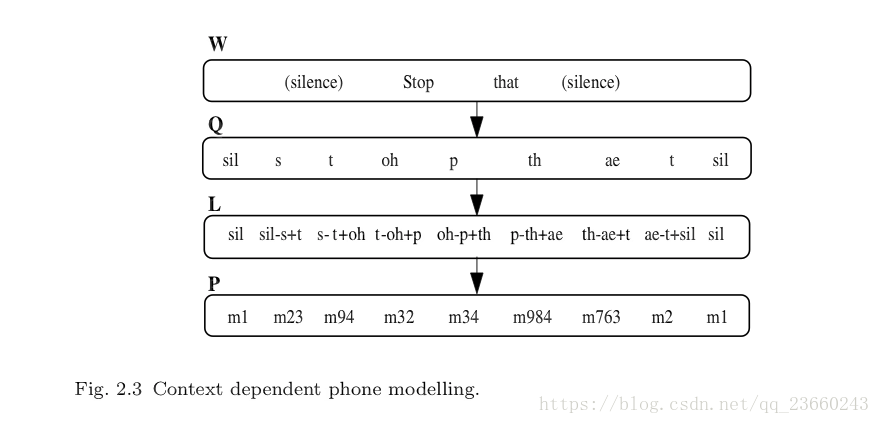
一個簡單的彌補這個問題的辦法就是把每個音素的左右兩個音素對也進行建模。我們把這種聲學建模稱之為triphone(三音素),如果有N個基本音素,那麼有N^3個潛在三音素(三個位置,每個位置N中可能,自己算一下)。為了避免結果資料發散(sparsity,對於這個我理解還不是很好,暫時把它看做對結果有壞影響的情況),邏輯上三音素的完整集合L可以通過分類然後把每個類的結果拿出從而得到一個實際的P個三音素模型(這裡可以推斷,P<L,減少了複雜度)。下圖介紹了我們的上述過程:
而引數狀態繫結如下圖:
其中x-q+y表示音素q的上下文:前一個音素為x,後一個音素為y。每一個基本音素的發音q都是參照發音詞典,然後根據上下文被對映成為邏輯上的音素,然後這些邏輯上的音素最終被對映成為物理上的模型。注意跨越單詞邊界的上下文依賴,這對於捕獲很多語音過程都很重要。比如在stop that中的p,在接下來的子音被突然抑制。
之所以我們把邏輯到現實模型的分類放在狀態層次而不是模型層次是因為:相較於後者前者更加簡單,同時能健壯的估計出更多的模型。關於狀態繫結一般的選擇都是選用決策樹演算法。每個音素q的每個狀態都有一個二叉樹與它關聯。樹的每個節點都攜帶者關於上下文的問題,為了分類音素q的狀態i,所有音素q的模型中的所有狀態i被劃分到一個pool中,並且處在樹的根節點。依賴於每個節點問題的答案,狀態池被連續切分直到變成葉子節點。每個葉子節點的所有狀態被繫結形成一個物理模型。在給定最終狀態繫結的情況下,最大化訓練資料相似度的問題通過從預定義的集合中選取(PS:這句想了好久,不知道如何翻譯最完美,放上原文:The questions at each node are selected from a predetermined set to maximise the likelihood of the training data given the final set of state-tyings)。如果狀態的輸出分佈是單高斯並且狀態的occupation counts知道的情況下,那麼我們可以在不使用訓練資料的情況下,可以很容易的在任何節點通過切分高斯來增加相似度。所以說,使用貪婪迭代的節點切分演算法,決策樹的成長將會非常高效。下圖說明了此演算法:
在途中,邏輯音素s-aw+n和t-aw+n被分配給了葉子節點3,所以在實際的模型中,他們分享相同的狀態。
使用音素驅使的決策樹來劃分狀態有很多好處,特別是,在訓練資料的時候所需但卻看不到的邏輯模型很容易被合成。一個缺點是分類可能會很粗糙,這個問題可以通過稱之為soft-tying 的方法削減。在這種框架下,一個後處理階段用來分組每個狀態和他相鄰的兩個狀態,並且彙集他們的高斯模型。因此,單高斯模型轉換成了混合高斯模型,但同時又保持了系統的高斯模型數量不變。
總結一下,目前語音識別的聲學建模的核心由繫結三個狀態的HMM模型集合,模型的輸出概率分佈為高斯分佈。主要步驟概括如下:
1. 單音素高斯HMM模型被建立,模型的均值和方差等於訓練資料的均值和方差,也稱作flat-start。
2. 單音素高斯模型的引數通過步驟3或者步驟4的EM迭代被估計。
3. 每一個單高斯單音素q對於訓練資料集中的每個不同的triphone x-q+y都拷貝複製一份。
4. 最終的訓練資料的結果集triphones被EM演算法又重新估計一遍,同時最後一次state occupation counts被記錄下來。
5. 對於每個音素中的每個狀態建立一個決策樹,訓練資料的triphones被對映為一個數量更少的繫結triphones,同時用EM演算法迭代重估計。
最終結果是所需要的繫結狀態的依賴於上下文的升學模型集。
PS:其實這一張感覺難點不少,初次看有很多不明白的地方,我只能強制自己先試圖理解,然後後面的章節如果有可能把這裡的坑解決,或者乾脆另外寫一個部落格解釋這裡的問題,希望對大家有幫助。