LLE原理及推導過程
所謂LLE即”local linear embedding”的降維演算法,在處理所謂的流形降維的時候,效果比PCA要好很多。下面介紹具體實現方法。
首先,所謂流形,我腦海裡最直觀的印象就是Swiss roll,我吃的時候喜歡把它整個攤開成一張餅再吃,其實這個過程就實現了對瑞士捲的降維操作,即從三維降到了兩維。降維前,我們看到相鄰的卷層之間看著距離很近,但其實攤開成餅狀後才發現其實距離很遠,所以如果不進行降維操作,而是直接根據近鄰原則去判斷相似性其實是不準確的。
LLE原理
LLE的原理其實是這樣的:
- 所謂區域性線性,就是認為在整個資料集的某小範圍內,資料是線性的,就比如雖然地球是圓的,但我們還是可以認為我們的籃球場是個平面;而這個“小範圍”,最直接的辦法就是k-近鄰原則。這個“近鄰”的判斷也可以是不同的依據:比如歐氏距離,測地距離等。
- 既然是線性,那麼對每個資料點
(D維資料,即
的列向量),可以用其k近鄰的資料點的線性組合來表示,即
- 。其中,
是
的列向量,
是
的第
行,
是
的第
個近鄰點。
- 通過使loss function最小化:
得到權重係數,一共
個數據點,對應
列
。
- 接下來是LLE中又一個假設:即認為將原始資料從D維降到d維後,
,其依舊可以表示為其k近鄰的線性組合,且組合係數不變,即
,再一次通過最小化loss function:
得到降維後的資料。
演算法推導
step 1:
運用k近鄰演算法得到每個資料的k近鄰點:
step 2: 求解權重係數矩陣
即求解:
在推導之前,我們首先統一下資料的矩陣表達形式
輸入:
權重:
則可逐步推匯出權重係數矩陣的表示式:
將看做區域性協方差矩陣, 那麼:
運用拉格朗日乘子法:
求導:
就上述表示式而言,區域性協方差矩陣
是個 的矩陣,其分母其實是
的逆矩陣的所有元素之和,而其分子是
的逆矩陣對行求和後得到的列向量。
step 3: 對映到低維空間
即求解:
低維空間向量:
首先,用一個 的稀疏矩陣(sparse matrix)
來表示
:
對 的近鄰點
:
;
否則:
因此:
其中,
是
方陣的第
列。所以
由矩陣論可知:對矩陣 ,有
所以:
再一次拉格朗日乘子法:
求導:
即
可見Y其實是M的特徵向量構成的矩陣,為了將資料降到 維,我們只需要取M的最小的
個非零特徵值對應的特徵向量,而一般第一個最小的特徵值接近0,我們將其捨棄,取前
個特徵值對應的特徵向量。
結果演示
藉助matlab強大的矩陣運算能力對swiss roll資料集進行了LLE降維。原始的資料如下:
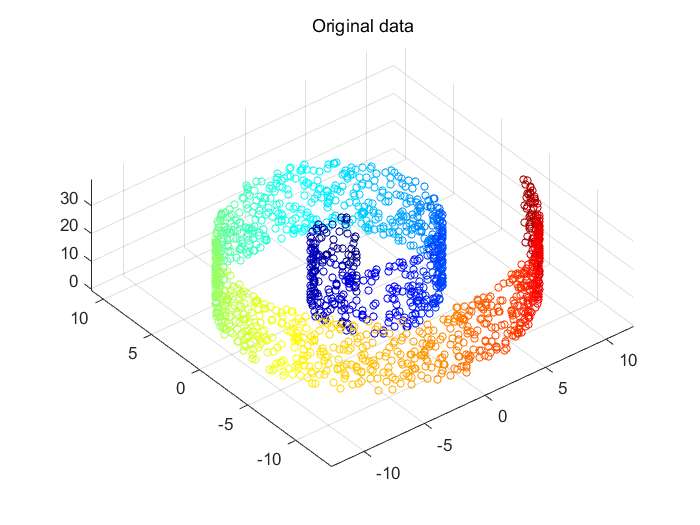
Fig.1. Swill roll資料集。
通過LLE降維後的結果如下:
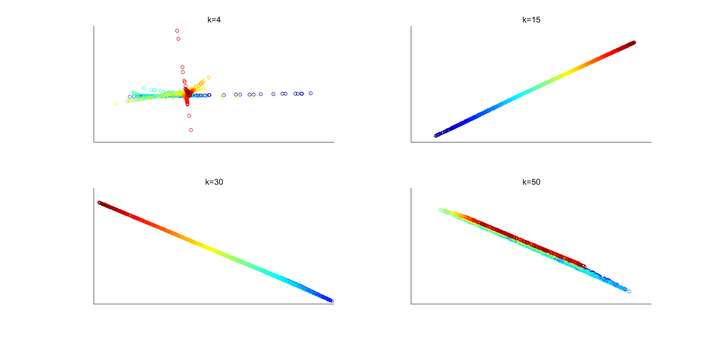
Fig. 2. LLE降維在不同k值的二維分佈結果。k代表在k近鄰演算法時選取的最近鄰個數。
可以看出,當k取值較小(k=4)時,演算法不能將資料很好地對映到低維空間,因為當近鄰個數太少時,不能很好地反映資料的拓撲結構。當k值取值適合,這裡選取的是k=15,可見不同顏色的資料能很好地被分開並保持適合的相對距離。但若k取值太大,如k=50,不同顏色的資料開始相互重疊,說明選取的近鄰個數太多則不能反映資料的流形資訊。
