協方差矩陣

協方差也只能處理二維問題，那維數多了自然就需要計算多個協方差，比如n維的資料集就需要計算n!(n−2)!∗2個協方差，那自然而然我們會想到使用矩陣來組織這些資料。給出協方差矩陣的定義：

這個定義還是很容易理解的，我們可以舉一個三維的例子，假設資料集有三個維度，則協方差矩陣為：

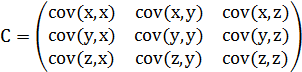
必須要明確一點，協方差矩陣計算的是不同維度之間的協方差，而不是不同樣本之間的。以下的演示將使用Matlab，為了說明計算原理，不直接呼叫Matlab的cov函式：

首先，隨機生成一個10*3維的整數矩陣作為樣本集，10為樣本的個數，3為樣本的維數。

>> mySample=fix(rand(10,3)*50)

mySample =

    40     7    32
    45    48     1
     6    47    42
    45    24    46
    31    40    33
     4     7    37
    13    21    37
    27    45    19
    47    39    32
    48    47     8

根據公式，計算協方差需要計算均值，前面特別強調了，協方差矩陣是計算不同維度之間的協方差，要時刻牢記這一點。樣本矩陣的每行是一個樣本，每列是一個維度，因此我們要按列計算均值。為了描述方便，我們先將三個維度的資料分別賦值：

>> dim1=mySample(:,1)

dim1 =

    40
    45
     6
    45
    31
     4
    13
    27
    47
    48

>> dim2=mySample(:,2)

dim2 =

     7
    48
    47
    24
    40
     7
    21
    45
    39
    47

>> dim3=mySample(:,3)

dim3 =

    32
     1
    42
    46
    33
    37
    37
    19
    32
     8
 

計算dim1與dim2，dim1與dim3，dim2與dim3的協方差：

>> cov12=sum((dim1-mean(dim1)).*(dim2-mean(dim2)))/(size(mySample,1)-1)

cov12 =

    78

>> cov13=sum((dim1-mean(dim1)).*(dim3-mean(dim3)))/(size(mySample,1)-1)

cov13 =

 -120.2444

>> cov13=sum((dim1-mean(dim1)).*(dim3-mean(dim3)))/(size(mySample,1)-1)

cov13 =

 -120.2444

>> cov13=sum((dim1-mean(dim1)).*(dim3-mean(dim3)))/(size(mySample,1)-1)

cov13 =

 -120.2444

>> cov23=sum((dim2-mean(dim2)).*(dim3-mean(dim3)))/(size(mySample,1)-1)

cov23 =

 -126.9444

協方差矩陣的對角線上的元素就是各個維度的方差，下面我們依次計算這些方差：

>> var1=std(dim1)^2

var1 =

  301.1556

>> var2=std(dim2)^2

var2 =

  268.9444

>> var3=std(dim3)^2

var3 =

  216.0111

這樣，我們就得到了計算協方差矩陣所需要的所有資料，可以呼叫Matlab的cov函式直接得到協方差矩陣：

>> cov(mySample)

ans =

  301.1556   78.0000 -120.2444
   78.0000  268.9444 -126.9444
 -120.2444 -126.9444  216.0111

計算的結果，和之前的資料填入矩陣後的結果完全相同。