七、函式和表格

通過使用 Python 中已有的函式，我們正在建立一個使用的技術清單，用於識別資料集中的規律和主題。 現在我們將探索Python程式語言的核心功能：函式定義。

我們在本書中已經廣泛使用了函式，但從未定義過我們自己的函式。定義一個函式的目的是，給一個計算過程命名，它可能會使用多次。計算中有許多需要重複計算的情況。 例如，我們常常希望對錶的列中的每個值執行相同的操作。

定義函式

double函式的定義僅僅使一個數值加倍。

# Our first function definition

def double(x):
    """ Double x """
    return
 
 2*x

我們通過編寫def來開始定義任何函式。 下面是這個小函式的其他部分（語法）的細分：

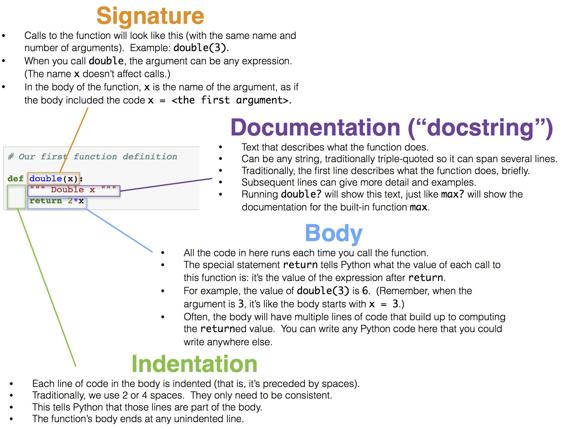
當我們執行上面的單元格時，沒有使特定的數字加倍，並且double主體中的程式碼還沒有求值。因此，我們的函式類似於一個菜譜。 每次我們遵循菜譜中的指導，我們都需要以食材開始。 每次我們想用我們的函式來使一個數字加倍時，我們需要指定一個數字。

我們可以用和呼叫其他函式完全相同的方式，來呼叫double。 每次我們這樣做的時候，主體中的程式碼都會執行，引數的值賦給了名稱x。

double(17)
34
double(-0.6/4)
-0.3

以上兩個表示式都是呼叫表示式。 在第二個裡面，計算了表示式-0.6 / 4

的值，然後將其作為引數x傳遞給double函式。 每個呼叫表示式最終都會執行double的主體，但使用不同的x值。

double的主體只有一行：

return 2*x

執行這個return語句會完成double函式體的執行，並計算呼叫表示式的值。

double的引數可以是任何表示式，只要它的值是一個數字。 例如，它可以是一個名稱。 double函式不知道或不在意如何計算或儲存引數。 它唯一的工作是，使用傳遞給它的引數的值來執行它自己的主體。

any_name = 42
double(any_name)
84

引數也可以是任何可以加倍的值。例如，可以將整個數值陣列作為引數傳遞給double

，結果將是另一個數組。

double(make_array(3, 4, 5))
array([ 6,  8, 10])

但是，函式內部定義的名稱（包括像double的x這樣的引數）只存在一小會兒。 它們只在函式被呼叫的時候被定義，並且只能在函式體內被訪問。 我們不能在double之外引用x。 技術術語是x具有區域性作用域。

因此，即使我們在上面的單元格中呼叫了double，名稱x也不能在函式體外識別。

x
---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
<ipython-input-18-401b30e3b8b5> in <module>()
----> 1 x

NameError: name 'x' is not defined

文件字串。 雖然double比較容易理解，但是很多函式執行復雜的任務，並且沒有解釋就很難使用。 （你自己也可能已經發現了！）因此，一個組成良好的函式有一個喚起它的行為的名字，以及文件。 在 Python 中，這被稱為文件字串 - 描述了它的行為和對其引數的預期。 文件字串也可以展示函式的示例呼叫，其中呼叫前面是>>>。

文件字串可以是任何字串，只要它是函式體中的第一個東西。 文件字串通常在開始和結束處使用三個引號來定義，這允許字串跨越多行。 第一行通常是函式的完整但簡短的描述，而下面的行則為將來的使用者提供了進一步的指導。

下面是一個名為percent的函式定義，它帶有兩個引數。定義包括一個文件字串。

# A function with more than one argument

def percent(x, total):
    """Convert x to a percentage of total.

    More precisely, this function divides x by total,
    multiplies the result by 100, and rounds the result
    to two decimal places.

    >>> percent(4, 16)
    25.0
    >>> percent(1, 6)
    16.67
    """
    return round((x/total)*100, 2)
percent(33, 200)
16.5

將上面定義的函式percent與下面定義的函式percents進行對比。 後者以陣列為引數，將陣列中的所有數字轉換為陣列中所有值的百分數。 百分數都四捨五入到兩位，這次使用round來代替np.round，因為引數是一個數組而不是一個數字。

def percents(counts):
    """Convert the values in array_x to percents out of the total of array_x."""
    total = counts.sum()
    return np.round((counts/total)*100, 2)

函式percents返回一個百分數的陣列，除了四捨五入之外，它總計是 100。

some_array = make_array(7, 10, 4)
percents(some_array)
array([ 33.33,  47.62,  19.05])

理解 Python 執行函式的步驟是有幫助的。 為了方便起見，我們在下面的同一個單元格中放入了函式定義和對這個函式的呼叫。

def biggest_difference(array_x):
    """Find the biggest difference in absolute value between two adjacent elements of array_x."""
    diffs = np.diff(array_x)
    absolute_diffs = abs(diffs)
    return max(absolute_diffs)

some_numbers = make_array(2, 4, 5, 6, 4, -1, 1)
big_diff = biggest_difference(some_numbers)
print("The biggest difference is", big_diff)
The biggest difference is 5

這就是當我們執行單元格時，所發生的事情。

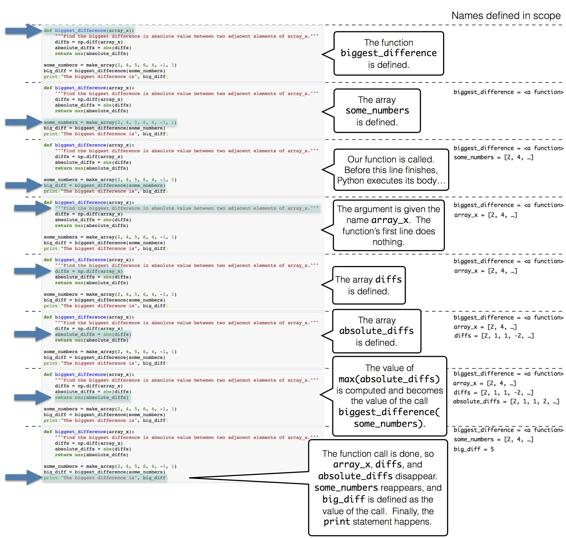
多個引數

可以有多種方式來推廣一個表示式或程式碼塊，因此一個函式可以有多個引數，每個引數決定結果的不同方面。 例如，我們以前定義的百分比percents，每次都四捨五入到兩位。 以下兩個參的數定義允許不同調用四捨五入到不同的位數。

def percents(counts, decimal_places):
    """Convert the values in array_x to percents out of the total of array_x."""
    total = counts.sum()
    return np.round((counts/total)*100, decimal_places)

parts = make_array(2, 1, 4)
print("Rounded to 1 decimal place: ", percents(parts, 1))
print("Rounded to 2 decimal places:", percents(parts, 2))
print("Rounded to 3 decimal places:", percents(parts, 3))
Rounded to 1 decimal place:  [ 28.6  14.3  57.1]
Rounded to 2 decimal places: [ 28.57  14.29  57.14]
Rounded to 3 decimal places: [ 28.571  14.286  57.143]

這個新定義的靈活性來源於一個小的代價：每次呼叫該函式時，都必須指定小數位數。預設引數值允許使用可變數量的引數呼叫函式;在呼叫表示式中未指定的任何引數都被賦予其預設值，這在def語句的第一行中進行了說明。 例如，在percents的最終定義中，可選引數decimal_places賦為預設值2。

def percents(counts, decimal_places=2):
    """Convert the values in array_x to percents out of the total of array_x."""
    total = counts.sum()
    return np.round((counts/total)*100, decimal_places)

parts = make_array(2, 1, 4)
print("Rounded to 1 decimal place:", percents(parts, 1))
print("Rounded to the default number of decimal places:", percents(parts))
Rounded to 1 decimal place: [ 28.6  14.3  57.1]
Rounded to the default number of decimal places: [ 28.57  14.29  57.14]

注：方法

函式通過將引數表示式放入函式名稱後面的括號來呼叫。 任何獨立定義的函式都是這樣呼叫的。 你也看到了方法的例子，這些方法就像函式一樣，但是用點符號來呼叫，比如some_table.sort(some_label)。 你定義的函式將始終首先使用函式名稱，並傳入所有引數來呼叫。

在列上應用函式

我們已經看到很多例子，通過將函式應用於現有列或其他陣列，來建立新的表格的列。 所有這些函式都以陣列作為引數。 但是我們經常打算，通過一個函式轉換列中的條目，它不將陣列作為它的函式。 例如，它可能只需要一個數字作為它的引數，就像下面定義的函式cut_off_at_100。

def cut_off_at_100(x):
    """The smaller of x and 100"""
    return min(x, 100)
cut_off_at_100(17)
17
cut_off_at_100(117)
100
cut_off_at_100(100)
100

如果引數小於或等於 100，函式cut_off_at_100只返回它的引數。但是如果引數大於 100，則返回 100。

在我們之前使用人口普查資料的例子中，我們看到變數AGE的值為 100，表示“100 歲以上”。 以這種方式將年齡限制在 100 歲，正是cut_off_at_100所做的。

為了一次性對很多年齡使用這個函式，我們必須能夠引用函式本身，而不用實際呼叫它。 類似地，我們可能會向廚師展示一個蛋糕的菜譜，並要求她用它來烤 6 個蛋糕。 在這種情況下，我們不會使用這個配方自己烘烤蛋糕， 我們的角色只是把菜譜給廚師。 同樣，我們可以要求一個表格，在列中的 6 個不同的數字上呼叫cut_off_at_100。

首先，我們建立了一個表，一列是人，一列是它們的年齡。 例如，C是 52 歲。

ages = Table().with_columns(
    'Person', make_array('A', 'B', 'C', 'D', 'E', 'F'),
    'Age', make_array(17, 117, 52, 100, 6, 101)
)
ages

Person	Age
A	17
B	117
C	52
D	100
E	6
F	101

應用

要在 100 歲截斷年齡，我們將使用一個新的Table方法。 apply方法在列的每個元素上呼叫一個函式，形成一個返回值的新陣列。 為了指出要呼叫的函式，只需將其命名（不帶引號或括號）。 輸入值的列的名稱必須是字串，仍然出現在引號內。

ages.apply(cut_off_at_100, 'Age')
array([ 17, 100,  52, 100,   6, 100])

我們在這裡所做的是，將cut_off_at_100函式應用於age表的Age列中的每個值。 輸出是函式的相應返回值的陣列。 例如，17 還是 17，117 變成了 100，52 還是 52，等等。

此陣列的長度與age表中原始Age列的長度相同，可用作名為Cut Off Age的新列中的值，並與現有的Person和Age列共存。

ages.with_column(
    'Cut Off Age', ages.apply(cut_off_at_100, 'Age')
)

Person	Age	Cut Off Age
A	17	17
B	117	100
C	52	52
D	100	100
E	6	6
F	101	100

作為值的函式

我們已經看到,Python 有很多種值。 例如，6是一個數值，"cake"是一個文字值，Table()是一個空表，age是一個表值（因為我們在上面定義）的名稱。

在 Python 中，每個函式（包括cut_off_at_100）也是一個值。 這有助於再次考慮菜譜。 蛋糕的菜譜是一個真實的東西，不同於蛋糕或配料，你可以給它一個名字，像“阿尼的蛋糕菜譜”。 當我們用def語句定義cut_off_at_100時，我們實際上做了兩件事情：我們建立了一個函式來截斷數字 100，我們給它命名為cut_off_at_100。

我們可以引用任何函式，通過寫下它的名字，而沒有實際呼叫它必需的括號或引數。當我們在上面呼叫apply時，我們做了這個。 當我們自己寫下一個函式的名字，作為單元格中的最後一行時，Python 會生成一個函式的文字表示，就像列印一個數字或一個字串值一樣。

cut_off_at_100
<function __main__.cut_off_at_100>

請注意，我們沒有使用引號（它只是一段文字）或cut_off_at_100()（它是一個函式呼叫，而且是無效的）。我們只是寫下cut_off_at_100來引用這個函式。

就像我們可以為其他值定義新名稱一樣，我們可以為函式定義新名稱。 例如，假設我們想把我們的函式稱為cut_off，而不是cut_off_at_100。 我們可以這樣寫：

cut_off = cut_off_at_100

現在cut_off就是函式名稱了。它是cut_off_at_100的相同函式。所以打印出的值應該相同。

cut_off
<function __main__.cut_off_at_100>

讓我們看看另一個apply的應用。

示例：預測

資料科學經常用來預測未來。 如果我們試圖預測特定個體的結果 - 例如，她將如何迴應處理方式，或者他是否會購買產品，那麼將預測基於其他類似個體的結果是很自然的。

查爾斯·達爾文（Charles Darwin）的堂兄弗朗西斯·高爾頓（Sir Francis Galton）是使用這個思想來基於數值資料進行預測的先驅。 他研究了物理特徵是如何傳遞下來的。

下面的資料是父母和他們的成年子女的身高測量值，由高爾頓仔細收集。 每行對應一個成年子女。 變數是家庭的數字程式碼，父母的身高（以英寸為單位），“雙親身高”，這是父母雙方身高的加權平均值 [1]，家庭中子女的數量 ，以及子女的出生次序（第幾個），性別和身高。

[1] 高爾頓在計算男性和女性的平均身高之前，將女性身高乘上 1.08。對於這個的討論，請檢視 Chance，這是一個由美國統計協會出版的雜誌。

# Galton's data on heights of parents and their adult children
galton = Table.read_table('galton.csv')
galton

family	father	mother	midparentHeight	children	childNum	gender	childHeight
1	78.5	67	75.43	4	1	male	73.2
1	78.5	67	75.43	4	2	female	69.2
1	78.5	67	75.43	4	3	female	69
1	78.5	67	75.43	4	4	female	69
2	75.5	66.5	73.66	4	1	male	73.5
2	75.5	66.5	73.66	4	2	male	72.5
2	75.5	66.5	73.66	4	3	female	65.5
2	75.5	66.5	73.66	4	4	female	65.5
3	75	64	72.06	2	1	male	71
3	75	64	72.06	2	2	female	68

（省略了 924 行）

收集資料的主要原因是，能夠預測父母所生的子女的成年身高，其中父母和資料集中的類似。讓我們嘗試這樣做，用雙親的身高作為我們預測的基礎變數。 因此雙親的身高是我們的預測性變數。

表格heights包含雙親和子女的身高。 兩個變數的散點圖顯示了正相關，正如我們對這些變數的預期。

heights = galton.select(3, 7).relabeled(0, 'MidParent').relabeled(1, 'Child')
heights

MidParent	Child
75.43	73.2
75.43	69.2
75.43	69
75.43	69
73.66	73.5
73.66	72.5
73.66	65.5
73.66	65.5
72.06	71
72.06	68

（省略了 924 行）

heights.scatter(0)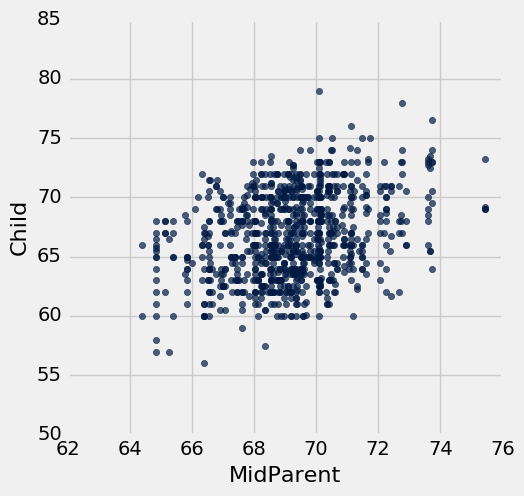

現在假設高爾頓遇到了新的一對夫婦，與他的資料集類似，並且想知道他們的子女有多高。考慮到雙親身高是 68 英寸，他預測子女身高的一個好方法是什麼？

一個合理的方法是基於約 68 英寸的雙親身高對應的所有點，來做預測。預測值等於從這些點計算的子女身高的均值。

假設我們是高爾頓，並執行這個計劃。現在我們只是對“68 英寸左右”的含義做一個合理的定義，並用它來處理。在課程的後面，我們將研究這種選擇的後果。

我們的“接近”的意思是“在半英寸之內”。下圖顯示了 67.5 英寸和 68.5 英寸之間的雙親身高對應的所有點。這些都是紅色直線之間的點。每一個點都對應一個子女；我們對新夫婦的子女身高的預測是所有子女的平均身高。這由金色的點表示。

忽略程式碼，僅僅專注於理解到達金色的點的心理過程。

heights.scatter('MidParent')
_ = plots.plot([67.5, 67.5], [50, 85], color='red', lw=2)
_ = plots.plot([68.5, 68.5], [50, 85], color='red', lw=2)
_ = plots.scatter(68, 66.24, color='gold', s=40)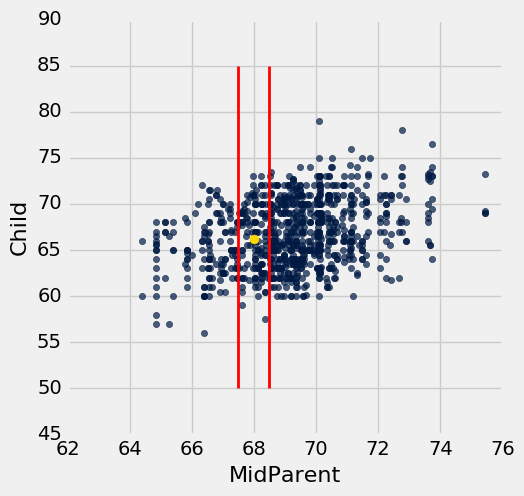

為了準確計算出金色的點的位置，我們首先需要確定直線之間的所有點。 這些點對應於MidParent在 67.5 英寸和 68.5 英寸之間的行。

close_to_68 = heights.where('MidParent', are.between(67.5, 68.5))
close_to_68

MidParent	Child
68.44	62
67.94	71.2
67.94	67
68.33	62.5
68.23	73
68.23	72
68.23	69
67.98	73
67.98	71
67.98	71

（省略了 121 行）

雙親身高為 68 英寸的子女的預測身高，是這些行中子女的平均身高。 這是 66.24 英寸。

close_to_68.column('Child').mean()
66.24045801526718

我們現在有了一種方法，給定任何資料集中的雙親身高，就可以預測子女的身高。我們可以定義一個函式predict_child來實現它。 除了名稱的選擇之外，函式的主體由上面兩個單元格中的程式碼組成。

def predict_child(mpht):
    """Predict the height of a child whose parents have a midparent height of mpht.

    The prediction is the average height of the children whose midparent height is
    in the range mpht plus or minus 0.5.
    """

    close_points = heights.where('MidParent', are.between(mpht-0.5, mpht + 0.5))
    return close_points.column('Child').mean() 

給定 68 英寸的雙親身高，函式predict_child返回與之前相同的預測（66.24 英寸）。 定義函式的好處在於，我們可以很容易地改變預測變數的值，並得到一個新的預測結果。

predict_child(68)
66.24045801526718
predict_child(74)
70.415789473684214

這些預測有多好？ 我們可以瞭解它，通過將預測值與我們已有的資料進行比較。 為此，我們首先將函式predict_child應用於Midparent列，並將結果收入稱為Prediction的新列中。

# Apply predict_child to all the midparent heights

heights_with_predictions = heights.with_column(
    'Prediction', heights.apply(predict_child, 'MidParent')
)
heights_with_predictions

MidParent	Child	Prediction
75.43	73.2	70.1
75.43	69.2	70.1
75.43	69	70.1
75.43	69	70.1
73.66	73.5	70.4158
73.66	72.5	70.4158
73.66	65.5	70.4158
73.66	65.5	70.4158
72.06	71	68.5025
72.06	68	68.5025

（省略了 924 行）

為了檢視預測值相對於觀察資料的位置，可以使用MidParent作為公共水平軸繪製重疊的散點圖。

heights_with_predictions.scatter('MidParent')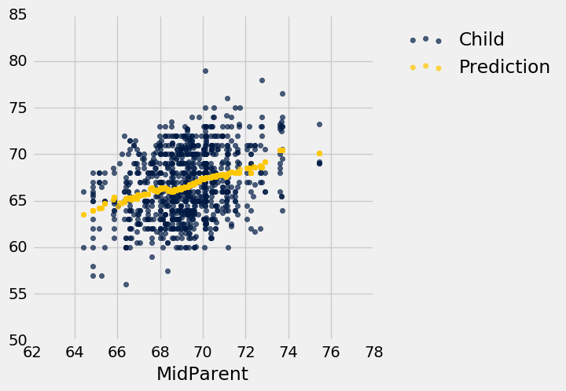

金色的點的圖形稱為均值圖，因為每個金色的點都是兩條直線的中心，就像之前繪製的那樣。每個都按照給定的雙親高度，做出了子女高度的預測。例如，散點圖顯示，對於 72 英寸的雙親高度，子女的預測高度將在 68 英寸和 69 英寸之間，事實上，predict_child(72)返回 68.5。

高爾頓的計算和視覺化與我們非常相似，除了他沒有 Python。他通過散點圖繪製了均值圖，並注意到它大致沿著直線。這條直線現在被稱為迴歸線，是最常見的預測方法之一。高爾頓的朋友，數學家卡爾·皮爾森（Karl Pearson）用這些分析來形式化關聯的概念。

這個例子，就像約翰·斯諾（John Snow）對霍亂死亡的分析一樣，說明了現代資料科學的一些基本概念的根源可追溯到一個多世紀之前。高爾頓的方法，比如我們在這裡使用的方法，是最近鄰預測方法的雛形，現在在不同的環境中有著有效的應用。機器學習的現代領域包括這些方法的自動化，來基於龐大且快速發展的資料集進行預測。

按照單變數分類

資料科學家經常需要根據共有的特徵，將個體分成不同的組，然後確定組的一些特徵。 例如，在使用高爾頓高度資料的例子中，我們看到根據父母的平均高度對家庭進行分類，然後找出每個小組中子女的平均身高，較為實用。

這部分關於將個體分類到非數值類別。我們從回顧gourp的基本用法開始。

計算每個分類的數量

具有單個引數的group方法計算列中每個值的數量。 結果中，分組列（用於分組的列）中的每個唯一值是一行。

這是一個關於冰淇淋圓通的小型資料表。 group方法可以用來列出不同的口味，並提供每種口味的計數。

cones = Table().with_columns(
    'Flavor', make_array('strawberry', 'chocolate', 'chocolate', 'strawberry', 'chocolate'),
    'Price', make_array(3.55, 4.75, 6.55, 5.25, 5.25)
)
cones

Flavor	Price
strawberry	3.55
chocolate	4.75
chocolate	6.55
strawberry	5.25
chocolate	5.25

cones.group('Flavor')

Flavor	count
chocolate	3
strawberry	2

有兩個不同的類別，巧克力和草莓。 group的呼叫會在每個類別中建立一個計數表。 該列預設稱為count，幷包含每個類別中的行數。

注意，這一切都可以從Flavor列中找到。Price列尚未使用。

但是如果我們想要每種不同風味的圓筒的總價格呢？ 這是group的第二個引數的作用。

發現每個類別的特徵

group的可選的第二個引數是一個函式，用於聚合所有這些行的其他列中的值。 例如，sum將累計與每個類別匹配的所有行中的價格。 這個結果中，分組列中每個唯一值是一行，但與原始表列數相同。

為了找到每種口味的總價格，我們再次呼叫group，用Flavor作為第一個引數。 但這一次有第二個引數：函式名稱sum。

cones.group('Flavor', sum)

Flavor	Price sum
chocolate	16.55
strawberry	8.8

為了建立這個新表格，group已經計算了對應於每種不同口味的，所有行中的Price條目的總和。 三個chocolate行的價格共計$16.55（你可以假設價格是以美元計量的）。 兩個strawberry行的價格共計8.80。

新建立的“總和”列的標籤是Price sum，它通過使用被求和列的標籤，並且附加單詞sum建立。

由於group計算除了類別之外的所有列的sum，因此不需要指定必須對價格求和。

為了更詳細地瞭解group在做什麼，請注意，你可以自己計算總價格，不僅可以通過心算，還可以使用程式碼。 例如，要查詢所有巧克力圓筒的總價格，你可以開始建立一個僅包含巧克力圓筒的新表，然後訪問價格列：

cones.where('Flavor', are.equal_to('chocolate')).column('Price')
array([ 4.75,  6.55,  5.25])
sum(cones.where('Flavor', are.equal_to('chocolate')).column('Price'))
16.550000000000001

這就是group對Flavor中每個不同的值所做的事情。

# For each distinct value in `Flavor, access all the rows
# and create an array of `Price`

cones_choc = cones.where('Flavor', are.equal_to('chocolate')).column('Price')
cones_strawb = cones.where('Flavor', are.equal_to('strawberry')).column('Price')

# Display the arrays in a table

grouped_cones = Table().with_columns(
    'Flavor', make_array('chocolate', 'strawberry'),
    'Array of All the Prices', make_array(cones_choc, cones_strawb)
)

# Append a column with the sum of the `Price` values in each array

price_totals = grouped_cones.with_column(
    'Sum of the Array', make_array(sum(cones_choc), sum(cones_strawb))
)
price_totals

Flavor	Array of All the Prices	Sum of the Array
chocolate	[ 4.75 6.55 5.25]	16.55
strawberry	[ 3.55 5.25]	8.8

你可以用任何其他可以用於陣列的函式來替換sum。 例如，你可以使用max來查詢每個類別中的最大價格：

cones.group('Flavor', max)

Flavor	Price max
chocolate	6.55
strawberry	5.25

同樣，group在每個Flavor分類中建立價格陣列，但現在它尋找每個陣列的max。

price_maxes = grouped_cones.with_column(
    'Max of the Array', make_array(max(cones_choc), max(cones_strawb))
)
price_maxes

Flavor	Array of All the Prices	Max of the Array
chocolate	[ 4.75 6.55 5.25]	6.55
strawberry	[ 3.55 5.25]	5.25

實際上，只有一個引數的原始呼叫，與使用len作為函式並清理表格的效果相同。

lengths = grouped_cones.with_column(
    'Length of the Array', make_array(len(cones_choc), len(cones_strawb))
)
lengths

Flavor	Array of All the Prices	Length of the Array
chocolate	[ 4.75 6.55 5.25]	3
strawberry	[ 3.55 5.25]	2

示例：NBA 薪水

nba表包含了 2015~2016 年 NBA 球員的資料。 我們早些時候審查了這些資料。 回想一下，薪水以百萬美元計算。

nba1 = Table.read_table('nba_salaries.csv')
nba = nba1.relabeled("'15-'16 SALARY", 'SALARY')
nba

PLAYER	POSITION	TEAM	SALARY
Paul Millsap	PF	Atlanta Hawks	18.6717
Al Horford	C	Atlanta Hawks	12
Tiago Splitter	C	Atlanta Hawks	9.75625
Jeff Teague	PG	Atlanta Hawks	8
Kyle Korver	SG	Atlanta Hawks	5.74648
Thabo Sefolosha	SF	Atlanta Hawks	4
Mike Scott	PF	Atlanta Hawks	3.33333
Kent Bazemore	SF	Atlanta Hawks	2
Dennis Schroder	PG	Atlanta Hawks	1.7634
Tim Hardaway Jr.	SG	Atlanta Hawks	1.30452

（省略了 407 行）

（1）每支球隊為球員的工資支付了多少錢？

唯一涉及的列是TEAM和SALARY。 我們必須按TEAM對這些行進行分組，然後對這些分類的工資進行求和。

teams_and_money = nba.select('TEAM', 'SALARY')
teams_and_money.group('TEAM', sum)

TEAM	SALARY sum
Atlanta Hawks	69.5731
Boston Celtics	50.2855
Brooklyn Nets	57.307
Charlotte Hornets	84.1024
Chicago Bulls	78.8209
Cleveland Cavaliers	102.312
Dallas Mavericks	65.7626
Denver Nuggets	62.4294
Detroit Pistons	42.2118
Golden State Warriors	94.0851

（省略了 20 行）

（2）五個位置的每個中有多少個 NBA 球員呢？

我們必須按POSITION分類並計數。 這可以通過一個引數來完成：

nba.group('POSITION')

POSITION	count
C	69
PF	85
PG	85
SF	82
SG	96

（3）五個位置的每個中，球員平均薪水是多少？

這一次，我們必須按POSITION分組，並計算薪水的均值。 為了清楚起見，我們將用一張表格來描述位置和薪水。

positions_and_money = nba.select('POSITION', 'SALARY')
positions_and_money.group('POSITION', np.mean)

POSITION	SALARY mean
C	6.08291
PF	4.95134
PG	5.16549
SF	5.53267
SG	3.9882

中鋒是最高薪的職位，均值超過 600 萬美元。

如果我們開始沒有選擇這兩列，那麼group不會嘗試對nba中的類別列計算“平均”。 （“亞特蘭大老鷹”和“波士頓凱爾特人隊”這兩個字串是不可能平均）。它只對數值列做算術，其餘的都是空白的。

nba.group('POSITION', np.mean)

POSITION	PLAYER mean	TEAM mean	SALARY mean
C	6.08291
PF	4.95134
PG	5.16549
SF	5.53267
SG	3.9882

交叉分類

通過多個變數的交叉分類

當個體具有多個特徵時，有很多不同的對他們分類的方法。 例如，如果我們有大學生的人口資料，對於每個人我們都有專業和大學的年數，那麼這些學生就可以按照專業，按年份，或者是專業和年份的組合來分類。

group方法也允許我們根據多個變數劃分個體。 這被稱為交叉分類。

兩個變數：計算每個類別偶對的數量

more_cones表記錄了六個冰淇淋圓筒的味道，顏色和價格。

more_cones = Table().with_columns(
    'Flavor', make_array('strawberry', 'chocolate', 'chocolate', 'strawberry', 'chocolate', 'bubblegum'),
    'Color', make_array('pink', 'light brown', 'dark brown', 'pink', 'dark brown', 'pink'),
    'Price', make_array(3.55, 4.75, 5.25, 5.25, 5.25, 4.75)
)

more_cones

Flavor	Color	Price
strawberry	pink	3.55
chocolate	light brown	4.75
chocolate	dark brown	5.25
strawberry	pink	5.25
chocolate	dark brown	5.25
bubblegum	pink	4.75

我們知道如何使用group，來計算每種口味的冰激凌圓筒的數量。

more_cones.group('Flavor')

Flavor	count
bubblegum	1
chocolate	3
strawberry	2

但是現在每個圓筒也有一個顏色。 為了將圓筒按風味和顏色進行分類，我們將把標籤列表作為引數傳遞給group。 在分組列中出現的每個唯一值的組合，在生成的表格中都佔一行。 和以前一樣，一個引數（這裡是一個列表，但是也可以是一個數組）提供了行數。

雖然有六個圓筒，但只有四種風味和顏色的唯一組合。 兩個圓筒是深褐色的巧克力，還有兩個粉紅色的草莓。

more_cones.group(['Flavor', 'Color'])

Flavor	Color	count
bubblegum	pink	1
chocolate	dark brown	2
chocolate	light brown	1
strawberry	pink	2

兩個變數：查詢每個類別偶對的特徵

第二個引數聚合所有其他列，它們不在分組列的列表中。

more_cones.group(['Flavor', 'Color'], sum)

Flavor	Color	Price sum
bubblegum	pink	4.75
chocolate	dark brown	10.5
chocolate	light brown	4.75
strawberry	pink	8.8

三個或更多的變數。 你可以使用group，按三個或更多類別變數對行分類。 只要將它們全部包含列表中，它是第一個引數。 但是由多個變數交叉分類可能會變得複雜，因為不同類別組合的數量可能相當大。

資料透視表：重新排列group的輸出

交叉分類的許多使用只涉及兩個類別變數，如上例中的Flavor和Color。 在這些情況下，可以在不同型別的表中顯示分類結果，稱為資料透視表（pivot table）。 資料透視表，也被稱為列聯表（contingency table），可以更容易地處理根據兩個變數進行分類的資料。

回想一下，使用group來計算每個風味和顏色的類別偶對的圓筒數量：

more_cones.group(['Flavor', 'Color'])

Flavor	Color	count
bubblegum	pink	1
chocolate	dark brown	2
chocolate	light brown	1
strawberry	pink	2

使用Table的pivot方法可以以不同方式展示相同資料。暫時忽略這些程式碼，然後檢視所得表。

more_cones.pivot('Flavor', 'Color')

Color	bubblegum	chocolate	strawberry
dark brown	0	2	0
light brown	0	1	0
pink	1	0	2

請注意，此表格顯示了所有九種可能的風味和顏色偶對，包括我們的資料中不存在的偶對，比如“深棕色泡泡糖”。 還要注意，每個偶對中的計數都出現在表格的正文中：要找到淺棕色巧克力圓筒的數量，用眼睛沿著淺棕色的行看，直到它碰到巧克力一列。

group方法接受兩個標籤的列表，因為它是靈活的：可能需要一個或三個或更多。 另一方面，資料透檢視總是需要兩個列標籤，一個確定列，一個確定行。

pivot方法與group方法密切相關：group將擁有相同值的組合的行分組在一起。它與group不同，因為它將所得值組織在一個網格中。 pivot的第一個引數是列標籤，包含的值將用於在結果中形成新的列。第二個引數是用於行的列標籤。結果提供了原始表的所有行的計數，它們擁有相同的行和列值組合。

像group一樣，pivot可以和其他引數一同使用，來發現每個類別組合的特徵。名為values的第三個可選引數表示一列值，它們替換網格的每個單元格中的計數。所有這些值將不會顯示，但是；第四個引數collect表示如何將它們全部彙總到一個聚合值中，來顯示在單元格中。

用例子來澄清這一點。這裡是一個透視表，用於尋找每個單元格中的圓筒的總價格。

more_cones.pivot('Flavor', 'Color', values='Price', collect=sum)

Color	bubblegum	chocolate	strawberry
dark brown	0	10.5	0
light brown	0	4.75	0
pink	4.75	0	8.8

這裡group做了同一件事。

more_cones.group(['Flavor', 'Color'], sum)

Flavor	Color	Price sum
bubblegum	pink	4.75
chocolate	dark brown	10.5
chocolate	light brown	4.75
strawberry	pink	8.8

儘管兩個表中的數字都相同，但由pivot生成的表格更易於閱讀，因而更易於分析。 透視表的優點是它將分組的值放到相鄰的列中，以便它們可以進行組合和比較。

示例：加州成人的教育和收入

加州的開放資料門戶是豐富的加州生活的資訊來源。 這是 2008 至 2014 年間加利福尼亞州教育程度和個人收入的資料集。資料來源於美國人口普查的當前人口調查。

對於每年，表格都記錄了加州的Population Count（人口數量），按照年齡，性別，教育程度和個人收入，構成不同的組合。 我們將只研究 2014 年的資料。

full_table = Table.read_table('educ_inc.csv')
ca_2014 = full_table.where('Year', are.equal_to('1/1/14 0:00')).where('Age', are.not_equal_to('00 to 17'))
ca_2014

Year	Age	Gender	Educational Attainment	Personal Income	Population Count
1/1/14 0:00	18 to 64	Female	No high school diploma	H: 75,000 and over	2058
1/1/14 0:00	65 to 80+	Male	No high school diploma	H: 75,000 and over	2153
1/1/14 0:00	65 to 80+	Female	No high school diploma	G: 50,000 to 74,999	4666
1/1/14 0:00	65 to 80+	Female	High school or equivalent	H: 75,000 and over	7122
1/1/14 0:00	65 to 80+	Female	No high school diploma	F: 35,000 to 49,999	7261
1/1/14 0:00	65 to 80+	Male	No high school diploma	G: 50,000 to 74,999	8569
1/1/14 0:00	18 to 64	Female	No high school diploma	G: 50,000 to 74,999	14635
1/1/14 0:00	65 to 80+	Male	No high school diploma	F: 35,000 to 49,999	15212
1/1/14 0:00	65 to 80+	Male	College, less than 4-yr degree	B: 5,000 to 9,999	15423
1/1/14 0:00	65 to 80+	Female	Bachelor’s degree or higher	A: 0 to 4,999	15459

（省略了 117 行）

表中的每一行對應一組年齡，性別，教育程度和收入。 總共有 127 個這樣的組合！

作為第一步，從一個或兩個變數開始是個好主意。 我們只關注一對：教育程度和個人收入。

educ_inc = ca_2014.select('Educational Attainment', 'Personal Income', 'Population Count')
educ_inc

Educational Attainment	Personal Income	Population Count
No high school diploma	H: 75,000 and over	2058
No high school diploma	H: 75,000 and over	2153
No high school diploma	G: 50,000 to 74,999	4666
High school or equivalent	H: 75,000 and over	7122
No high school diploma	F: 35,000 to 49,999	7261
No high school diploma	G: 50,000 to 74,999	8569
No high school diploma	G: 50,000 to 74,999	14635
No high school diploma	F: 35,000 to 49,999	15212
College, less than 4-yr degree	B: 5,000 to 9,999	15423
Bachelor’s degree or higher	A: 0 to 4,999	15459

（省略了 117 行）

我們先看看教育程度。 這個變數的分類已經由不同的收入水平細分了。 因此，我們將按照教育程度分組，並將每個分類中的人口數量相加。

education = educ_inc.select('Educational Attainment', 'Population Count')
educ_totals = education.group('Educational Attainment', sum)
educ_totals

Educational Attainment	Population Count sum
Bachelor’s degree or higher	8525698
College, less than 4-yr degree	7775497
High school or equivalent	6294141
No high school diploma	4258277

教育程度只有四類。 計數太大了，檢視百分比更有幫助。 為此，我們將使用前面章節中定義的函式percents。 它將數值陣列轉換為輸入陣列總量的百分比陣列。

def