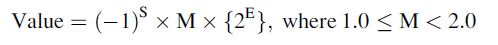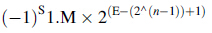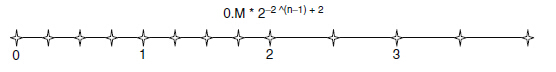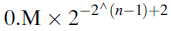本部分來自於《大規模並行處理器程式設計實戰》第六章、第七章。打算不再看這本書了，準備看《programming massively parallel processors 2nd》，即它的第二版，第一版是09年的，第二版是13年的，雖說第二版可是裡面涉及的是cuda4.0 和5.0，然而現在2015年7月，cuda都7.0了，正所謂趕速度，完全趕不上啊。雖然說本書好，不過一個不小心，你費老大勁做的優化，發現其實新版本的cuda或者硬體完全不需要，果然有關cuda的最好的資料其實還是官方文件，因為這些完全趕不上速度啊。

一、效能優化

        CUDA kernel函式的執行速度很大程度上取決於每個裝置的資源約束。而且不同的應用程式中，不同的約束可能決定併成為限制因素。在特定的CUDA裝置上，可以通過一種資源代替另一種資源來提高英程式的效能。合理的策略有可能提高效能，也可能不起作用，所以需要測試，本章說的這些可以用來培養程式設計師對演算法的直覺，如何來提高整體的效能。

1.1 執行緒執行問題

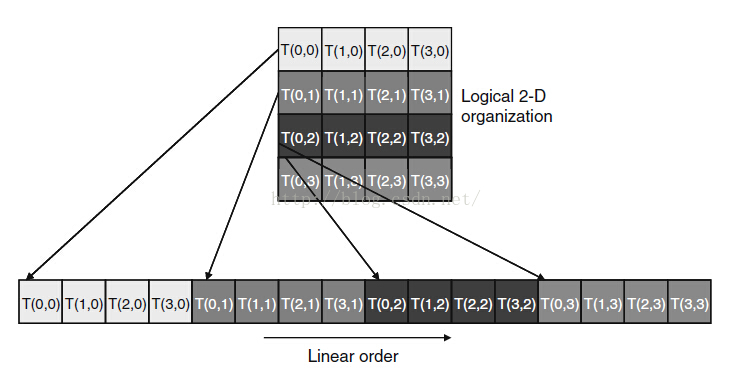
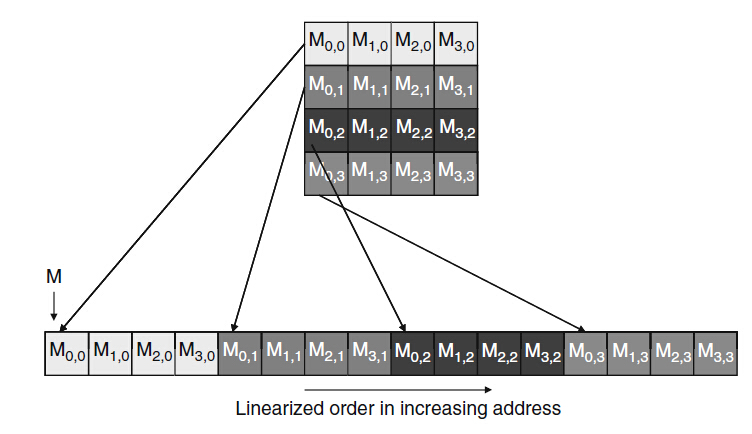
        相比較前面幾個博文，沒有過多的討論每個塊中執行緒的執行時間問題。在本書發售的時候，Nvidia公司是通過對塊中的執行緒進行捆綁執行的，即執行的不是單個執行緒而是一個warp（包含32個執行緒），這樣做降低硬體成本，而且一定程度上優化了儲存器訪問的服務。對於劃分warp來說，如果是一維的，那麼對於最後一個warp的劃分如果不滿32個，會將其他塊中的執行緒拉過來補全成32個再執行。如果對於多維執行緒的塊來說，劃分warp前會把維度對映成一個線性順序，y 和z 的座標小的放前面，大的放後面。假如一個塊有二維的執行緒，那麼將所有threadIdx.y是1的執行緒放在threadIdx.y是0的執行緒後面（注意這裡是y 不是x，即按照 Fortran語言的順序，前面的變化快，後面的變化慢），以此類推（這裡要注意這種訪問形式，在後面的1.2很有用，相當於二維的矩陣是轉置的，不是正常的那種形式，注意，不過如果將y想象成矩陣的行，x想像成矩陣的列，那就沒問題了）。

圖1

上圖就是將二維的執行緒塊對映成一維的順序形式。（注意順序）。而對於三維的塊來說，首先將threadIdx.z為0的所有執行緒按照線性順序排列，以此類推。將warp中所有執行緒執行玩一個指令，再去執行另一個指令，這種執行方式叫做SIMT（single Instruction multiple thread，單指令多執行緒）。如果在一個warp中所有的執行緒執行的是相同的指令，那麼工作效率最高，如果說在if-then-else結構中，決策條件基於threadIdx的值，比如if（threadIdx>2）｛｝這種的，那麼會導致執行緒分支，即按照兩個控制流分支路徑，這樣執行緒0、1、2和3、4、5就不同；如果迴圈條件基於threadIdx的值，則迴圈也會引起執行緒分支。這種用法自然會導致很多重要的並行演算法的產生。

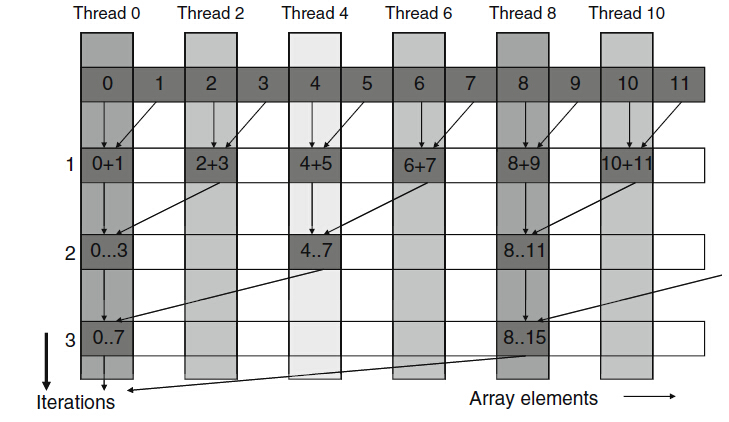
        這裡舉個歸約陣列和的演算法：即對於一個有著N個元素的陣列來說，想要求的所有元素的和，那麼歸約採取的是兩兩結合，即假如10個元素（(1,2),(3,4),(5,6),(7,8),(9,10)），然後第二次（（1,2,3,4）,(5,6,7,8),(9,10)）。這種型別的，兩兩歸約，因為前面計算一次之後就只有10/2=5個數值，所以第二次只需要計算5/2=2次（每次執行完一次，再重新分配，比如前面的第二次（9,10）因為缺少2個，就無法被4整除，所以第二次只計算了2次，然後（1,2,3,4,5,6,7,8）,(9,10)）接著最後得到最終答案；程式碼如下：

1.__shared__float partialSum[]

2.unsigned int t = threadIdx.x;
3.for(unsigned int stride = 1;
4.    stride < blockDim.x; stride *= 2)
5.{
6.__syncthreads();
7.if(t %( 2 * stride) == 0)
8.   partialSUm[t] += paritialSum[t + stride];
9.}

執行過程如下：

圖2

注意：上述的歸約其實導致塊中有一般的執行緒從來不執行，是很浪費的，所以需要修改kernel函式，留待作業。

在上面的程式碼中，就是當threadIdx.x的值為偶數的時候才執行加法，所以會導致那些不執行第8行程式碼的執行緒需要通過另外一條路徑。下面是修改的kernel函式，即不再採用兩兩相加的方法，這樣的是具有較少執行緒分支的kernel函式：

1.__shared__float partialSum[]

2.unsigned int t = threadIdx.x;
3.for(unsigned int stride = blockDim.x>>1;
4.    stride > 0; stride >>= 1)
5.{
6.__syncthreads();
7.if(t < stride)
8.   partialSUm[t] += paritialSum[t + stride];
9.}

修改之後的程式碼的效能有所不同，上述程式碼中通過移位來代替除法操作，降低開銷。執行過程如下：

圖3

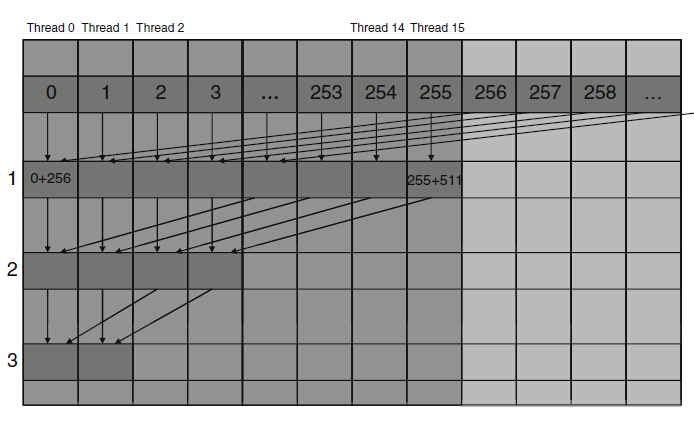
因為第一次迭代中，執行緒0-255都執行加法，而執行緒256-511不執行加法。由於warp中包含的32個執行緒對應的threadIdx.x值是連續的，因此都0-7個warp所有執行緒都執行加法，第8-15個warp則跳過加法，由於warp中所有執行緒都通過相同的路徑，所以沒有執行緒分支。可是還是因為有if的存在，kernel函式的分支並未完全消除。在執行第5次迭代的時候，第8行程式碼的執行緒個數低於32.也就是，最後5次迭代中分別只有16、8、4、2、1個執行緒執行加法運算，所以仍然存在分支。

1.2全域性儲存器的頻寬
        制約CUDA kernel函式的一個重要因素就是全域性儲存器的訪問資料。之前有討論過如何減少訪問的流量來達到加速的目的，這裡接著討論儲存器合併技術。使得更加有效的將資料從全域性儲存器中移動到共享儲存器和暫存器上。因為cuda系統採用的是DRAM的全域性儲存器，這種DRAM單元為了加快資料訪問的速度，採用並行程序的方式，即當DRAM晶片中的感測器接收到請求的單元的索引的時候，會順帶把其附近的單元的電位一起傳送過來，如果應用程式在訪問單元改變前能夠充分利用這種來自多個連續單元的資料，則會比真正的隨機順序的單元訪問要塊得多。所以需要kernel函式安排資料的訪問順序。（本書釋出時，現在不知道cuda的裝置還是不是採用DRAM）在G80/GT200中，考慮這樣一個事實：同一個waro中的執行緒在任何給定的時間內都執行同一條指令，也就是說當同一個wari中所有執行緒執行同一條指令訪問全域性儲存器中的連續單元時，這種訪問模式是最好的。如執行緒0訪問單元N（N應該是與16個字的邊界對齊，也就是說，N的低16位應該為0），執行緒1訪問單元N+1,以此類推。那麼所有的這些訪問請求將會被合併和結合成對所有連續單元的單個請求，使得DRAM在傳輸資料的速度接近全域性儲存器頻寬的峰值。

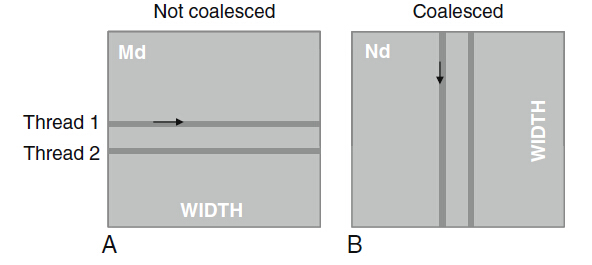
圖4

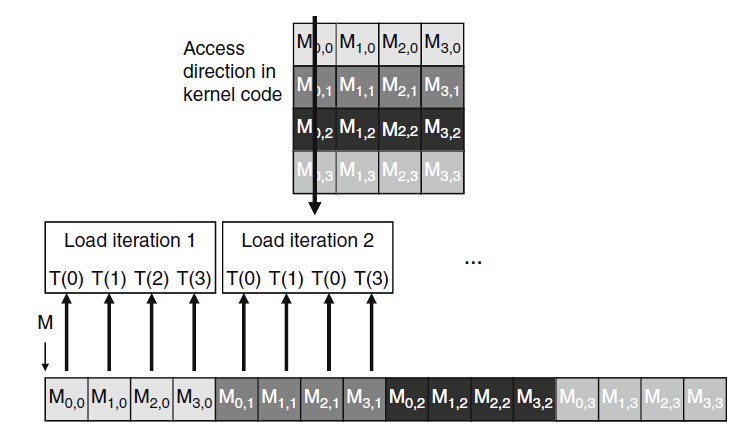
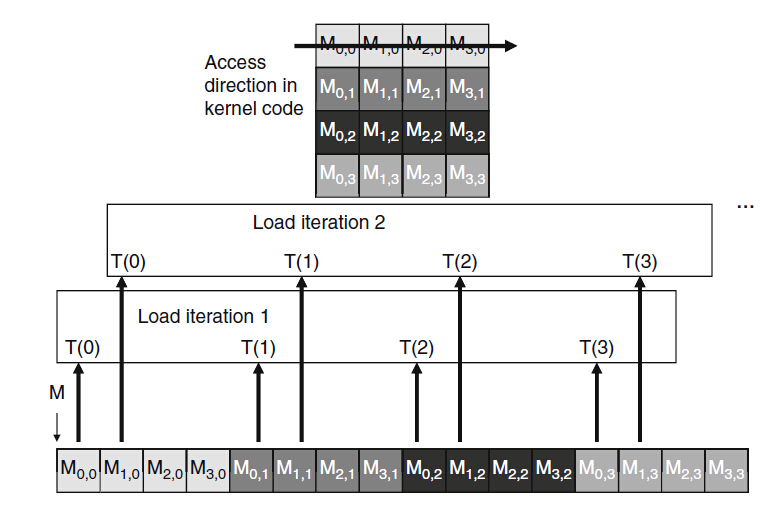
上圖為合併前和後的訪問圖。假設合併前，同一個warp中所有執行緒第0次迭代時訪問0-31行中第0列的元素，第1次迭代訪問0-31行中第1列的元素，這樣沒法合併；可以第0次迭代的時候第0個warp中的執行緒讀取第0-31列的第0行元素。為何這樣更有利，這需要了解矩陣元素在全域性儲存器中是如何存放的。

       在全域性儲存器中其實和主機記憶體一樣，地址是線性的，也就是如果全域性儲存器包含1024個單元，那麼訪問地址其實是0-1023.對於GT200來說，其地址範圍為0-2^32-1。在C和CUDA中矩陣元素都是以行為主的約定存放的，即如下圖形式：

圖5

M(0,0)和M(0,1)之間隔了4個元素

圖6

上圖中，在第1次迭代中，同一個warp中執行緒由迴圈發起訪問矩陣中所有列的第0個元素。因為所有列的第0個元素存放在全域性儲存器中連續的單元中。這樣硬體檢測到，就會合併成一個綜合的訪問，這樣DRAM就支援高速的資料訪問；下面就是合併前的訪問形式：

圖7

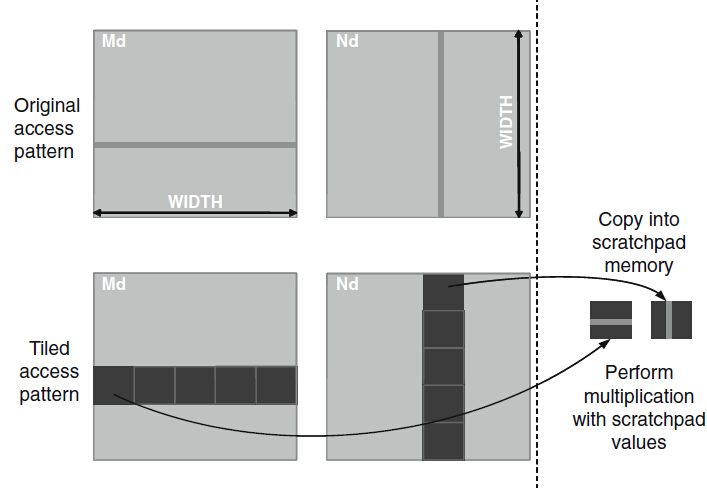
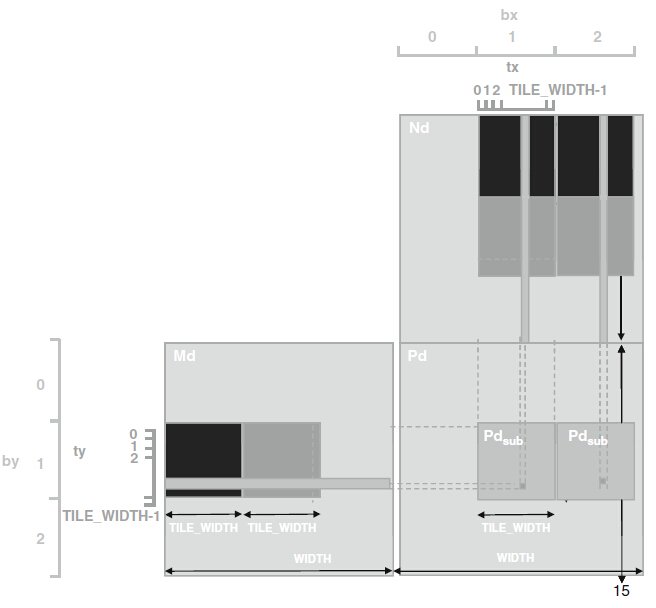
下面是個矩陣乘法的技術，如果說演算法本身要求kernel函式以行的方式遍歷資料，那麼可以使用共享儲存器來實現儲存空間合併，先通過執行緒協作方式，即以合併的方式載入資料到共享儲存器，然後在共享儲存器上不管是以行還是列都不會引起效能的太大差異，因為共享儲存器本身能實現告訴的片上儲存器，無需通過合併來提高資料的訪問速度。

圖8

__global__ void MatrixMulKernel(float* Md,float* Nd,float* Pd, int Width)
{
1.__shared__ float Mds[TILE_WIDTH][TILE_WIDTH];
2.__shared__ float Nds[TILE_WIDTH][TILE_WIDTH];

3.int bx = blockIdx.x;  int by = blockIdx.y;
4.int tx = threadIdx.x; int ty = threadIdx.y;

//標識要處理的Pd元素對應的行和列
5.int Row = by * TILE_WIDTH + ty;
6.int Col = bx * TILE_WIDTH + tx;

7.float Pvalue = 0;
//迴圈Md和Nd中要計算Pd元素的塊
8.for(int m = 0; m < Width/TILE_WITDH; ++m){

//相互協作把Md和Nd的塊載入到共享儲存器中
9.    Mds[ty][tx] = Md[Row * Width + (m * TILE_WITDH + tx)];
10.   Nds[ty][tx] = Nd[(m * TILE_WIDTH + ty) * Width + Col];
11.   __syncthreads();

12.for(int k = 0;k <TILE_WITDH; ++k)
13.   Pvalue += Mds[ty][k] * Nds[k][tx];

14.Pd[Row][Col] = Pvalue;
  }
}

（個人：注意ty，tx的順序，因為tx變化快，而且剛好矩陣在儲存器中是行儲存的，剛好對上）上述程式碼是使用共享儲存器的分塊矩陣乘法的kernel。在第10行Nd的索引的所有項對於warp中所有執行緒都有相同的值（最先變化的是tx，在本博文最上面說了），除了Col中的tx項，即同一個warp中所有執行緒對應的tx值是相鄰的；所以一個warp中相鄰的執行緒訪問一行中相鄰的元素，會將它們合併（個人：方法就是先固定ty，假設只有tx是變數，然後觀察訪問的全域性儲存器的地址是否相鄰即可）（個人：這裡的Mds和Nds都是按照塊讀取的，即一次是讀取一個矩陣，不是單獨的Md行和Nd列，參考上面那個圖的形式）。

1.3 SM資源的動態劃分
    SM中的執行資源有暫存器、執行緒塊槽和執行緒槽。比如在GT200中每個SM支援1024個執行緒槽，每個槽容納一個執行緒，執行時劃分這些執行緒槽給執行緒塊，如果每個執行緒塊有256個執行緒，就將1024個執行緒槽劃分給4個塊，如果每個執行緒塊有128個執行緒，就劃分1024個執行緒槽給8個執行緒塊。這種是動態劃分，不是固定劃分。所以有好處也有壞處，壞處是會導致資源限制之間有輕微的相互影響，導致資源利用率降低，因為SM中塊槽支援8個，所以最多容納8個塊，算下來每個塊至少要有128個執行緒才能充分利用。

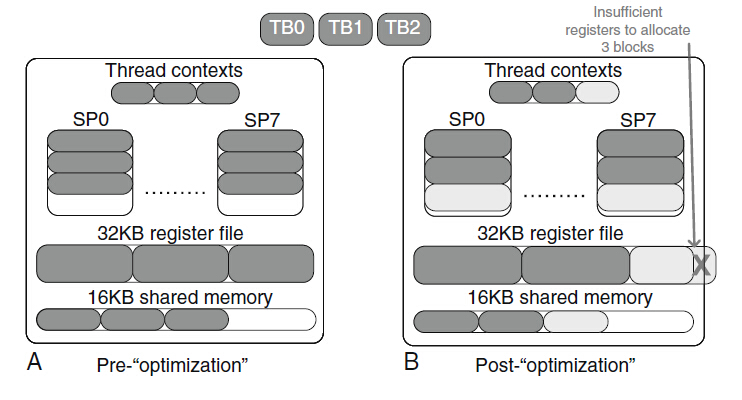
        暫存器檔案是另一種動態劃分的資源。在每個CUDA裝置中，暫存器的數量不是在程式設計模型中指定的，而是在實現中可變的。比如G80的每個SM支援8192個暫存器檔案。比如kernel中每個執行緒使用10個暫存器，那麼塊大小為16*16，那麼一個塊用到16*16*10=2560個。那麼每個SM中按照暫存器的限制只能放入3個塊，所以會導致總的執行緒為768個，雖然這時候塊槽和執行緒槽都不是限制因素。假如每個執行緒使用11個暫存器，那麼總的三個快需要8448個暫存器，超過了暫存器限制，按照前面說的，SM通過減少塊的形式來處理（下圖b），所以使得暫存器數目減少16*16*11=2816，SM中只有兩個塊，執行緒也變成了512個進駐，也就是說，多使用一個自動變數（存放入暫存器），在G80上執行的程式中warp的並行性減少1/3。參考資源《cuda occupany calculatar，nvidia 2009》，這是一個可下載的excel表格，在給定kernel函式使用資源的情況下，對某個特殊的裝置實現可以計算出在每個SM上執行的執行緒的實際數量。

圖9.資源限制的相互影響

         不過在有的情況下可以通過增加自動變數提高單個執行緒的執行速度，因為將其放入暫存器中，就無需去訪問耗時的儲存器了，比如在kernel函式中，全域性儲存器的載入和使用有4個獨立的指令，在G80中，處理每條指令需要4個時鐘週期，所以這4條指令需要16個時鐘週期，如果全域性儲存器有200個時鐘週期的延時，為了充分利用執行單元，至少需要200/(4*4)=14個warp來保證零開銷排程。（即增加暫存器是為了加快執行時間）。假設將獨立指令數目從4增加到8，那麼間歇性訪問儲存器需要32個時鐘週期，如果全域性儲存器中還是200個時鐘週期的延時，那麼為了充分利用執行單元需要200/(4*8)=7個warp保證零開銷排程，也就是上面的即使塊數目從3減到2，此時warp的資料也從24減少到16，可是每個SM中仍有足夠的warp在執行，反而效能其實還是提高的。這種引數分配需要不斷的除錯，去測試，為了減少這種人力的趺粗。Ryoo等人提出了一種用於實現實驗過程自動化的方法（參考文獻見最下面）。

1.4資料預取

         通過使用之前介紹的分塊資料使用共享儲存器訪問解決全域性儲存器頻寬的限制問題，使得在一些warp在等待的時候，或者說只需要先計算一半，等剩下資料到了在計算另一半結果。而對於那些所有執行緒都等待其儲存器訪問結果的時候，這種方法也有不足了，即當所有執行緒在儲存器訪問指令和已訪問的資料使用指令之間的獨立指令很少，就會這樣。

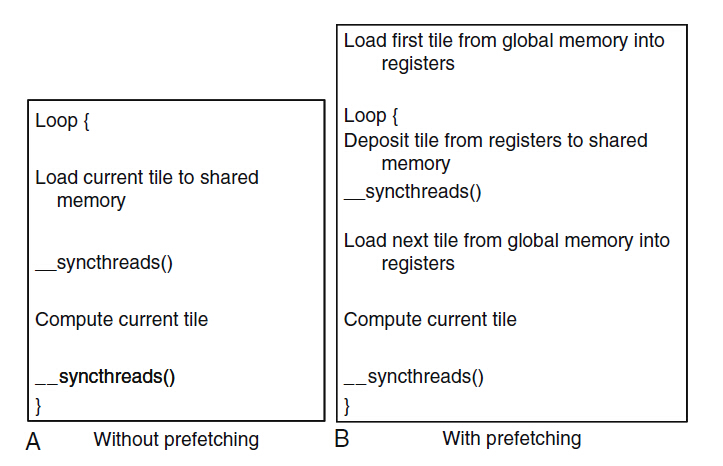
       一種方法解決上述問題是：當使用當前資料元素的時候預取下一個資料元素，通過預取技術和分塊技術的結合來解決頻寬限制和長延時的問題。如下圖：

圖10

         上圖A對應圖8的分塊矩陣乘法的kernel函式，對應的圖8下面的程式碼的第9，10行就是將當前塊載入到共享儲存器，不過第9行其實是執行了兩部分：將Md的元素從全域性儲存器的單元載入到暫存器；將暫存器的內容儲存到共享儲存器單元中。這兩部分之間沒有獨立的指令，所以那些載入當前塊的warp可能需要等待很長時間，之後才能計算當前塊，所以，可能需要很多的warp才能讓浮點單元保持忙碌。圖10中B就是修改的預取版本。在進入迴圈之前，將第一個塊載入到暫存器，進入迴圈後，將已載入的資料移動到共享儲存器中，對應圖8下面程式碼的第12和13行的點積迴圈，（個人，類似於cpp常寫的索引自加操作）當迴圈迭代時，這個當前迭代中“下一個塊”變成下一次迭代的“當前塊”。在執行點積迴圈在兩者之間增加很多獨立的指令，減少了執行緒必須等待全域性儲存器訪問資料的時間。雖然這樣用到額外的暫存器會減少SM上的塊，不過如果顯著減少了每個執行緒等待其全域性儲存器載入資料的時間，這技術還是有優勢的。

1.5指令混合

         在當前（本書的時間）的CUDA GPU 中，每個處理器的核心都只有有限的指令處理頻寬。不管是浮點計算還是載入指令還是分支指令，都需要佔用指令處理頻寬。

for(int k = 0;k < BLOCK_SIZE; ++k)
    Pvalue += Ms[ty][k] * Ns[k][tx];
   (a)迴圈引入指令開銷

Pvalue += Ms[ty][0] * Ns[0][tx]+ ...
            Ms[ty][15] * Ns[15][tx];
   (b)迴圈展開可以提高指令的混合水平

上面的程式碼中，對於（a）來說，迴圈引入的更新迴圈計數變數k 和每次迭代後的分支指令，而且在矩陣Ms和Ns的索引中用到迴圈技術變數k,會引入地址運算指令。相比較有2條浮點運算指令、迴圈分支指令、2條地址運算指令，1條迴圈增量計數指令。也就是說只有1/3的指令是執行浮點運算的 。所以這樣的效能限制在頻寬峰值的1/3以內。相比較下面的展開可以消除分支指令、迴圈計數和地址運算指令（常量偏移即可）。在未來（基於本書的時間），編譯器將會支援自動展開，不過在工具未成熟之前，還是需要在原始碼中展開的。

1.6 執行緒粒度
       在效能優化中一個重要的演算法決定因素是執行緒的粒度。應該儘可能的把更多工作放在每個執行緒中並採取更少的執行緒是有優勢的額，特別是執行緒之間有重複的工作時。

圖11 用矩形塊增大執行緒的粒度

上圖就是之前那個矩陣乘法的例子。執行緒粒度優化的可能性在於多個快重複的載入Md的每個塊。在之前的演算法中兩個塊生成Pd的兩個塊需要重複載入Md的同一行。如果將兩個執行緒塊合併成一個，就可以消除這種冗餘。在新的執行緒塊中，每個執行緒現在負責計算Pd的兩個元素。修改kernel使得函式一次可以計算兩個點積。兩個點積都使用相同的行Mds和不同的列Nds進行運算。這樣將全域性儲存器的訪問次數減少1/4。不過這樣做的負面效果就是新的kernel函式現在使用更多的暫存器和共享儲存器。因此，在SM上能執行的塊的數目也可能相應減少，執行緒塊的總數會減少一半，這對於維度較小的矩陣，會導致並行性不足。對於G80/G200中一個2048*2048的矩陣乘法，合併水平方向上4個相鄰的塊來計算水平方向上相鄰的塊，效能最好。

1.7可度量的效能

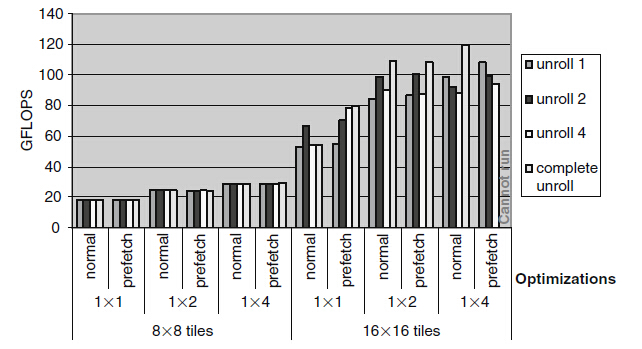
圖12 不同技術的效能度量

上述用到的技術有分塊、迴圈展開、資料預取和執行緒粒度，左邊的是8*8的塊，右邊是16*16的塊，每個塊的大小，比較了基礎程式碼、粒度調整中合併兩個塊後的程式碼和合並4個塊後的程式碼。結論是： 

       1）塊的大小在效能中起到主要作用。在塊大小未達到16*16時，迴圈展開和資料預取都不起作用。因為對於8*8的塊來說，全域性儲存器的頻寬處於飽和狀態。並且1*2的矩形分塊將全域性儲存器的訪問次數減少了1/4，而1*4的減少了3/8，不過在1*8的矩形塊只能減少7/16，因為使用更大的塊能提高的效能呈遞減趨勢，這使得加大塊的大小失去了吸引力。

      2）當塊的大小足夠大時（比如這裡的16*16）,那麼減輕全域性儲存器頻寬的飽和狀態，迴圈展開和資料預取就變得重要了。

     3）雖然資料預取對於1*1的塊有用，但是在1*2的矩形分塊中基本不起作用。對於1*4的矩形分塊，資料預期中一個16*16的塊需要使用的暫存器已經超過SM中暫存器的總數，這使得程式碼在G80上沒法執行。不過通過多種技術調整可以看出在G80上執行速度可以從18 GFLOPS增加到120 GFLOPS。

二、浮點運算

2.1浮點格式

        浮點標準有兩個IEEE-754（1985年）和IEEE 754-2008【IEEE，2008】，幾乎絕大部分計算機廠商都接受的。理解這些概念對於應用程式的開發還是很重要的。最開始，浮點數系統採用位模式來表示數值。在IEEE浮點標準中，一個數值的表示由3部分組成：符號位（S）、階碼（E）和尾數（M）。每個（S，E，M）模式根據下面的格式可以標識一個唯一的數值：

S代表的意義：當S=0時表示是一個正數，當S=1時表示一個負數。

這裡為了舉例容易點，假設每個浮點數包含1位符號位，3位階碼和2位尾數。例如，0.5D表示5*10^(-1)，0.1B表示1*2*(-1)。

2.1.1M的規範化表示

在上面的公式中，要求M的範圍為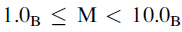。這使得對每個浮點數來說，它的尾數是唯一的。0.5D的唯一尾數就是M=1.0：

0.5D=1.0B*2(-1)

另一種表示為0.1B*2^0，不過根據表示規則，這種表示法的尾數值太小，10.0B*2^(-2)的尾數值太大。在這種限定下，每個浮點數只有一個符合規格的尾數值。滿足這種限制條件的數稱之為規格化數。因為所有的尾數值都滿足1.xx這種形式的限制條件，所以可以省略前面的"1."，比如0.5對應的尾數在兩位尾數表示法中為00，這是1.00中省略1.得到的。也就是在IEEE中，n位的尾數其實可以有效的表示（n+1）位尾數的值。

2.1.3 E的餘碼表示

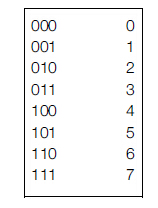
       E的位數決定了數的表示範圍。IEEE標準採用E的編碼約定。如果階碼E採用n位表示，那麼對於階碼在二進位制補碼錶示法的基礎上再加上（2^(n-1)-1）構成它的餘碼表示法。二進位制補碼採取這樣的方式來表示，即負數的補碼是通過對值的每位取反，在加1得到的。例如對於三位階碼來說，在使用補碼之後加上的是2^(3-1)-1 = 011.即-1的餘碼是先去符號，為001，然後取反110，加1 111，然後加上011，結果為010.

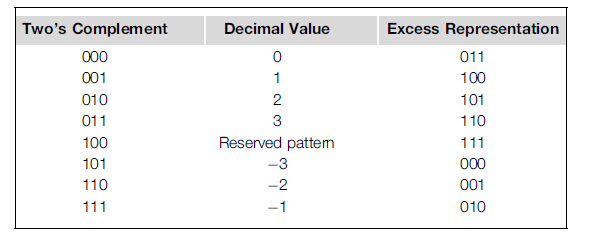
      餘碼的表示法的好處是在無符號比較器上可以用來比較有符號數。如圖

圖12.按照二進位制補碼的順序排序的餘3碼（二進位制補碼、十進位制值、餘碼表示）

如上圖，當吧3位餘碼看做無符號數時，它可以表示的數值在-3到3之間單調遞增。-3的餘碼是000,3的餘碼是110，所以如果用無符號比較器比較餘3碼001和100的大小，那麼001要比100小，這對於硬體實現是一個期望的屬性，因為無符號比較器比有符號比較器小，而且速度快。

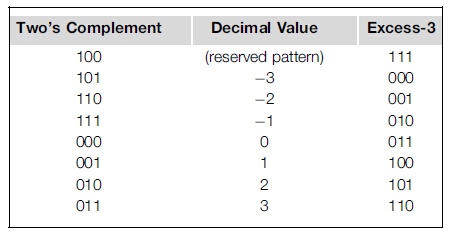
圖13 按照餘碼的順序排序餘3碼

現在用6位的格式來表示0.5D：

0.5D=001000，其中S=0，E=010，M=1.00（或者00，省略1.）

也就是說0.5D的6位表示形式是001000.

一般來說，如果採取的是規格化的尾數和餘碼表示的階碼，那麼帶n位階碼的數對應的值為：

2.2能表示的數

         一種數值格式所能表示的數是指在這種格式中能精確表示的數值。例如，3位無符號整形表示格式所能的數如下圖

圖14 3位無符號格式所能表示的數；數軸表示法

在這種格式中，-1和9都不能表示。下圖為目前為止能表示的所有數值及兩種變換形式。為了有效控制表的大小，採用的格式是5位。這種格式中包含位符號位S，2位階碼（採用1位餘碼編碼），2位尾數M（省略了1.）。非零列給出了目前為止討論過的格式所能表示的數。這種格式不能表示0這個數。

圖15 非0、下溢位和非規範化格式所有表示的數

圖16非0表示法的表示的數

在圖16中就是圖15中的能夠表示的正數，負數是相對0對稱的，所以省略。從這個數軸中，的5條結論：

       1）能表示的數之間的主間隔取決於階碼位。在圖16中，在0的每一邊都有3個主間隔，這是因為階碼有兩位。主間隔基本上位於2的冪之間，由於階碼有2位，因此這兩位階碼可以形成3個不停的冪（2^-1=0.5D,2^0=1.0D,2^1=2.0D），每個都是能表示的數的間隔的開始。

       2）每個間隔中能表示的數的個數取決於尾數位。如果尾數位2位，則在每個間隔內能表示4個數。一般而言，如果尾數為N位，則在每個間隔內能表示2^N個數。如果一個要表示的值落在其中的一個間隔內，舍入後它就成為間隔內一個可表示的數。所以，每個間隔內能表示的數的個數越多，在這個區間中要表示的數也越精確。所以，尾數的位數決定了表示的精度。

      3）這種格式不能表示0.。

      4）越靠近0的地方，可表示的數離得越近。向0方向移動，每個間隔是前一個間隔的一半。能表示的數之間離得越近，表示數時就越準確。

      5）在0附近，能表示的數出現了空白。這是因為規格化的尾數對應的範圍已經把0排除掉。當要表示0-0.5之間的數時，引入的誤差遠遠大於（4倍）0.5-1.0這些更大的數之間引入的誤差。一般而言，在這種表示法中，如果尾數的位數為N，那麼接近0的間隔內引入的誤差要比下一個間隔內引入的誤差大2^N倍。對於基於非常小的資料值且依賴於收斂條件的準確檢測的數值演算法，這種缺陷會導致執行時不穩定且結果不準確。比如在除法中，表示這些很小的數時引入的誤差在除法過程中，會被放大很多倍。

      在規格化浮點數系統中，一種可以容納0的方法是下溢位（abrupt underflow）約定，如圖15第2列，當階碼位E=0是，對應的數是0。在5位的格式中，這種方法在0附近提出了8個能表示的數（4個正數 4個負數），把它們都設定成0.雖然這種方法能表示0，但在0附近能表示的數之間出現了更大的空白，如下圖：

圖17 下溢位格式能表示的數

顯然，與圖16相比，這些數值演算法的準確性依賴於0附近較小數的準確表示。

圖18非規格化格式能表示的數

       實際上，IEEE標準採用的是非規格化的方法。這種方法在0附近放寬了對規格化資料的要求。如圖15，當E=0時，不再假定尾數是1.xx這種形式，假定它是0.xx形式。階碼所表示的值與之前的間隔仍相同。例如，在圖15中，非規格化數00001的階碼位00，尾數位01,。假定尾數是0.01，而階碼值與之前間隔的階碼值相同：是0而不是-1.也就是說，00001所表示的值是0.01*2^0=2^(-2)。圖18展示了非規格化格式所能表示的數。現在，在0附近所能表示的數之間是均勻的間隔。從直觀上看，非規格化約定吧在非0表示法中最後一個間隔內能表示的4個數分散開，用於彌補0附近的空白區域。這樣就可以消除前面兩種方法中不期望出現的空白。注意，在最後兩個間隔中能表示的數之間的距離相同。一般而言，如果n位的階碼是0，那麼這個值是

總之，浮點數表示法的精度取決於引入的最大誤差，這種誤差是要表示一個浮點數時，將它轉化成能夠表示的數而引入的誤差。誤差越小，精度越高。尾數的位數增加，可以提供浮點數表示法的精度。將圖18中能表示的數增加一位尾數，可以將最大誤差減少一半，從而提高精度。因此，一個數值系統用的尾數的位數越多，它的精度也越高。

2.3 特殊的位模式與精度

      在IEEE中，如果階碼的所有位都是1，而尾數為0，那麼該數表示一個無窮大的值。如果尾數不為0，表示NaN（not a number）。

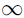
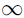
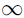
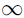
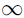
其他的所有數都是規格化的浮點數。單精度的浮點數有1位符號位（S）、8位階碼（E）和23位尾數（M）。雙精度的浮點數則有1位符號位（S）、11位階碼（E）和52位尾數（M）。與單精度的浮點數格式相比，由於雙精度浮點數的尾數多29位，因此可表示的數的最大誤差減少到1/(2^29)！由於多了3位階碼，因此雙精度浮點數格式也擴充套件了該區間能夠表示的數的個數。這也擴充套件了能表示的數值範圍，能表示非常大和非常小的數。所有能表示的數都落在-（負無窮大）到+（正無窮大）之間。溢位時可能會出現（如除以0）。任何能表示的數除以+或者-，結果都是0.

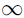
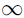
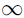
       其輸入值沒有意義的操作產生一個NaN--如0/0、0*、/、-。它們也用於表示一些資料。這些資料在程式中沒有正確的初始化。在IEEE標準中NaN有兩種型別：signaling和quiet。signaling NaN（SNaN）通過最重要的尾數位清零來表示，而quiet NaN則通過設定最重要的尾數位來表示。如果用一個signaling NaN作為算術運算操作的輸入，則會引起異常。例如（1.0+SNaN）。只有說程式設計師希望在浮點計算過程中確保，只要使用任何NaN值時，程式就會中斷執行，這時候signaling NaN才能使用。這時候意味著程式在執行過程中出錯了。在執行關鍵任務的應用程式中，在沒有通過單獨的方式進行執行過程的有效性驗證前，這種執行過程沒法繼續。例如，軟體工程師常用signaling NaN來標記所有沒有初始化的資料。這種實踐確保在執行過程中檢測所使用的哪些資料沒有初始化。目前的GPU硬體（2010年的時候）還不支援signaling NaN，這是因為在大規模並行執行過程中，支援準確的signaling NaN是有難度的。

       quiet NaN在作為算術運算操作的輸入時得到的額結果是quiet NaN。例如，操作（1.0+quiet NaN）得到的結果是一個quiet NaN。quiet NaN 常用的如下的應用程式中，：使用者可以預先知道程式的執行結果，並在通過不同的輸入時可以得到更為有效的結果時，決定是否要重新執行程式。當輸出結果時，quiet NaN是以“NaN”的形式輸出，因此使用者就能在輸出檔案中很容易的找到它們。這也是在CUDA應用程式中如何檢測資料損壞的方法。

2.4算術運算的準確度和舍入

         當兩個輸入操作上要進行浮點加法或減法運算時，而兩者的階碼不同時，需要將階碼較小的運算元的尾數右移。比如（1.00*2^1）+(1.00*2^(-2))。因為階碼不同，所以先右移結果為（1.00*2^1）+(0.001*2^1)。理論上結果為1.001，可是在5位表示法中沒法表示，所以按照硬體的位數，最好的就是產生一個非常接近的表示的數1.01*2^1.這樣引入了（0.001*2^1）的誤差。這個誤差是最低有效位的一般。稱這個誤差為0.5 ULP（unit in the last place）.如果用於算術和舍入操作的硬體很完美，那麼引入最大的誤差也不會超過0.5 ULP。不過在某些更復雜的硬體算術運算單元中，都是通過迭代逼近演算法實現的，比如分段函式和超越函式。不過在更新的GPU中算術運算顯然要比之前的準確的多。

2.5演算法的優化

     在計算數學中有個知識點就是在比如求和的時候，需要先對不同的數進行排序，或者說對不同的數的加法有順序，這就是為了防止大數吃小數，先讓最小的數不斷的相加，就像滾雪球一樣，這樣才能不使得最後的結果丟失了小數，這也是為什麼在大規模的並行數值演算法中頻繁的使用排序的重要原因。

ps：1、SIMT和SIMD是兩種不同的實現技術，在CPU中的SSE（streaming SIMD extensions，單指令多資料擴充套件）。在SSE實現中，一條指令處理多個數據元素，先收集資料再將資料打包到單個的暫存器中，如果有嚴格對齊需求，則程式設計師需要用到額外的指令。在SIMT中，所有執行緒都在自己的暫存器中處理資料，減輕了資料收集和打包方面的負擔。在SIMT中，選擇控制流分支相對於SSE也要簡單很多，不需要程式設計師用額外的指令來處理控制流。

        2、（書本當前時間）未來的cuda社保會為全域性儲存器中的資料提供更大容量的片上快取，這種快取會自動合併kernel函式中的訪問模式，程式設計師會很少需要手動重新排列它們的訪問模式，不過在目前的1億次和仍在使用的上一代cuda裝置中，這種合併技術仍然還是很有用的。

       3、Ryoo, S., Rodrigues, C. I., Baghsorkhi, S. S., & Stone, S. S. (2008). Optimization principles and application performance evaluation of a multithreaded GPU using CUDA. In Proceedings of the 13th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming (pp. 73–82). Salt Lake City, UT. 

             Ryoo, S., Rodrigues, C. I., Stone, S. S., Baghsorkhi, S. S., Ueng, S. Z.,Stratton, J. A., et al. (2008). Program pruning for a multithreaded GPU. In Code generation and optimization: Proceedings of the Sixth Annual IEEE/ACM International Symposium on code generation and optimization (pp. 195–204). Boston, MA.