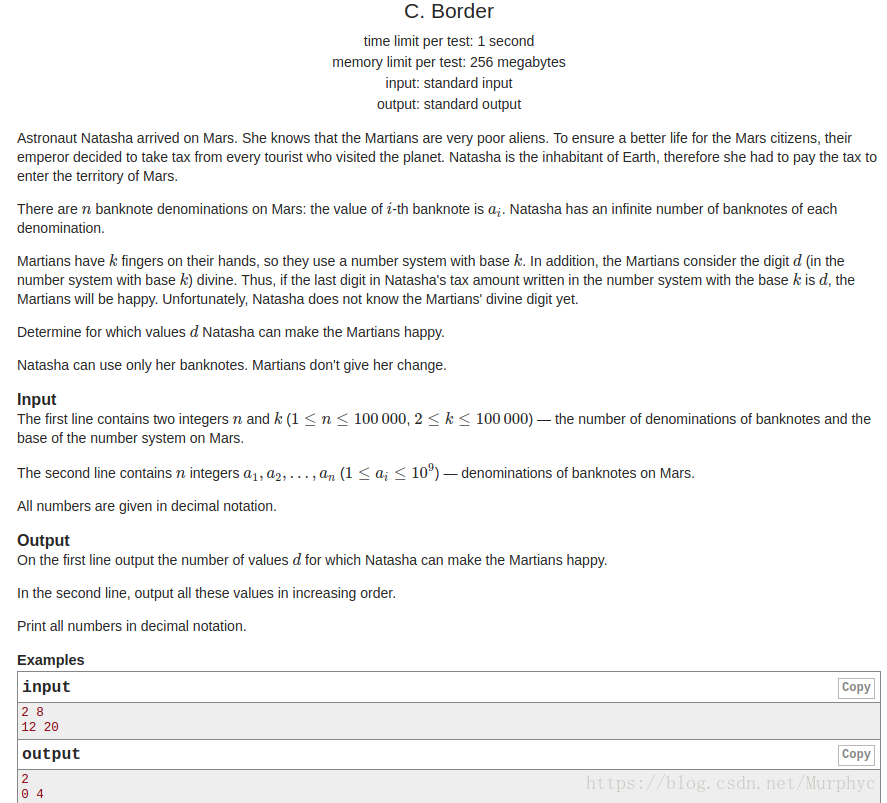
Codeforces Round #499 (Div. 1) C. Border

                Codeforces Round #499 (Div. 2) E. Border

                                         (數論/貝祖定理）

題意：給你n個數字(十進位制)，每個數字都可以使用無限次，問你在k進位制下，可以組合的到的目標和的尾數有哪些.

昨天下午打完多校感覺還是蠻累的，cf晚上11點的場子也不大想打，剛好室友想開小號隨便打打，

我也就幫忙讀了個題順便嘴炮ac了一下(´･ω･｀)

看到這道E的時候馬上就想到了可以得到的尾數僅和用以組合的數的有關，昨晚是這麼(不嚴謹的)想的，

假設個數字的為，那麼便可以發現對於所有的個數都有

那麼對於目標和來說相當於

最後的尾數則是

然後我就猜了一下正解就是

早上簡單寫了一下果然A了o(*≧▽≦)ツ

對於,那麼任意都滿足為的整數倍

特別的，必定存在滿足

做一個小推廣，那麼便可以得到對於n個數字()的必定存在滿足如下等式的的集合

如果已知該定理，那麼這道題就變的很簡單了,正解就是如我不嚴謹的猜測一樣為：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

#define inf int(0x3f3f3f3f)
#define mod int(1e9+7)
#define eps double(1e-6)
#define pi acos(-1.0)
#define lson  root << 1
#define rson  root << 1 | 1

int main()
{
    int n,k;
    scanf("%d%d",&n,&k);
    int gcd=k;
    for(int i=0;i<n;i++)
    {
        int x;
        scanf("%d",&x);
        gcd=__gcd(gcd,x%k);
    }
    int cnt=0;
    printf("%d\n",k/gcd);
    while(cnt<k)
    {
        printf("%d ",cnt);
        cnt+=gcd;
    }
    printf("\n");
}