1、概述

    huffman編碼是一種可變長編碼（  VLC：variable length coding)）方式，於1952年由huffman提出。依據字元在需要編碼檔案中出現的概率提供對字元的唯一編碼，並且保證了可變編碼的平均編碼最短，被稱為最優二叉樹，有時又稱為最佳編碼。

2、原理

在瞭解huffman樹為最優二叉樹時，先要明確下面幾個概念：

    路徑長度:樹中一個節點到另一個節點之間分支構成這兩個節點之間的路徑，路徑上的分支數目為其路徑長度。

    樹的路徑長度:樹根到每一個節點的路徑長度之和 為 “l”。

     節點的帶權路徑長度:節點到樹根之間的路徑長度與節點上權的乘積。

                                                                                                          n

     樹的帶權路徑長度:所有節點的帶權路徑長度之和，記作 WPL = ∑wk  *  lk 。

                                                                                                         k=1

    n個節點，權值為{ w1,  w2, - - -,w

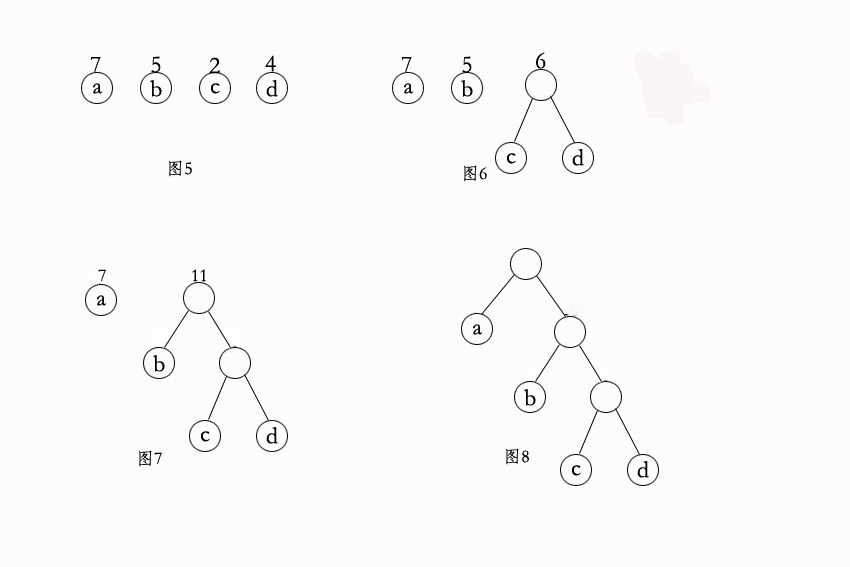
取節點a,b,c,d 其w[] = {2, 5, 7, 4}，a=7 構造如下三棵樹為例：

  圖1：wpl = 7*2 +5*2 + 2*2 + 4*2 = 36

  圖2：wpl = 7*3 + 5*3 + 2*1 + 4*2 = 46

  圖3：wpl = 7*1 + 5*2 + 2*3 + 4*3 = 35

可以證明（圖3）其帶權路徑長度最短，就是huffman樹。依次為兩節點的連線線編碼，左孩子為0，右孩子為1。那麼圖3就變成了（圖33）：

  編碼如下：a（0）、b（10）、c（110）、d（111）

  不知道是否有人會問為什麼a、b、c、d都是樹的葉子節點，而不存在某個是父節點呢？試想，如果a是c、d的父節點，假設a的編碼為0，其左右孩子是b、c，那麼b，c的編碼分別是00，和01，那麼當出現諸如010001的壓縮串時，可分別解釋為caac，cbc，因為在出現a時，如果後面的編碼為0，則不確定是解釋為aa還是b了，出現歧義就出問題，所以字元只能出現在葉子節點。

  在上面我們必須保證須編碼的字元必須出現葉子節點，那我們怎麼保證（圖33）就是最短帶權路徑呢？我們下面一步步走下去構造huffman樹，我們還假設a、b、c、d的帶權為7、5、2，4。

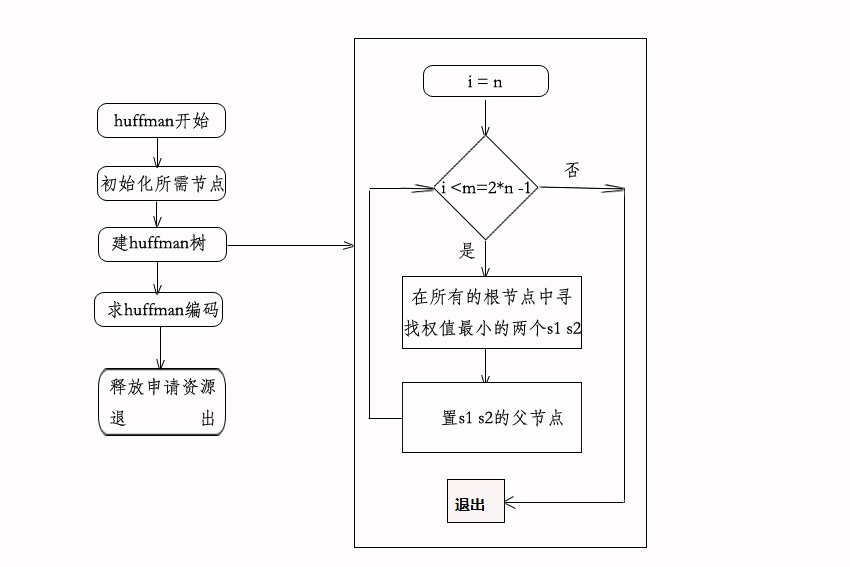
3、構造huffman樹過程

構造huffman樹的哈夫曼演算法如下：

  （1）n節點的權值｛w1、w2、·····，wn｝構成n棵二叉樹集合F=｛T1，T2，···，Tn｝，每棵二叉樹Ti只有一個帶權為Wi的根節點，左右孩子均空。

  （2）在F中選取兩棵根節點權值最小的作為樹的左右孩子構造一棵新的二叉樹，且置根節點的權值為左右孩子權值之和，在F中刪除這兩棵樹，新二叉樹之於F中

  （3）重複（2），直到F中只有一棵樹為止，這棵樹就是huffman樹。

  上面就是以abcd四個節點構造huffman樹的過程。

4、huffman程式碼（如下）

// Huffman coding.cpp : 定義控制檯應用程式的入口點。
//Copyright@Qyee, 2011-7-30

#include "stdafx.h"
#include <iostream>
#include <Windows.h>

using namespace std;

//huffman tree節點定義
typedef struct
{
	int weight;					//儲存權值
	int parent, lchild, rchild;	//儲存左右孩子的節點值
}HuffmanNode, *HuffmanTree;

typedef char **HuffmanCode;

void HuffmanCoding(HuffmanTree &HT, int *w, int n);	//Huffman編碼函式
void select(HuffmanTree HT,int n, int &s1, int &s2);//選擇書中節點值較小的兩個節點
void Error(char* message);		//顯示錯誤資訊

int w[] = {2, 5, 7, 4};	//各節點權值

int main(int argc, char* argv[])
{
	HuffmanTree HT;

	HuffmanCoding(HT, w, 6);

	getchar();	//在win7系統，防止直接跳出，接收字元才執行return語句
	return 0;
}

void HuffmanCoding(HuffmanTree &HT, int *w, int n)
{
	if (n <= 1)
		Error("code is small");
	int m = 2 * n - 1; //n nodes create huffman tree need 2n-1 nodes
	HT = (HuffmanNode*)malloc((m + 1) * sizeof(HuffmanNode));//Huffman tree的所有節點

	int s1, s2; //record the two mini weights nodes

	memset(HT, 0, (m + 1)* sizeof(HuffmanNode));	//對所有節點初始化為-0
	//set the n nodes
	for (int i = 1; i <= n; i++)
	{
		HT[i].weight = *w++;	//初始化各節點權值
	}

	//建立Huffman tree
	for(int i = n + 1; i <= m; ++i)
	{
		//選擇剩餘節點中權值較小的s1和s2
		select(HT, i - 1, s1, s2);
		HT[s1].parent = i;
		HT[s2].parent = i;
		HT[i].lchild = s1;
		HT[i].rchild = s2;
		HT[i].weight = HT[s1].weight + HT[s2].weight;
	}

	HuffmanCode HC;
	int start, c, f;
	HC = (HuffmanCode)malloc((n + 1) * sizeof(char*));
	char* cd = (char*)malloc(n * sizeof(char));
	cd[n - 1] = '\0';
	for(int i = 1; i <= n; ++i)
	{
		start = n - 1;
		for(c = i, f = HT[i].parent; f != 0; c = f, f = HT[f].parent)
			if (HT[f].lchild == c)
				cd[--start] = '0';
			else
				cd[--start] = '1';
		HC[i] = (char*)malloc((n - start) * sizeof(char));
		strcpy(HC[i], &cd[start]);
	}

	for (int i = 1; i <= n; i++)
	{
		cout<<HC[i]<<endl;
	}

	free(cd);
	free(HC);
	free(HT);
}

void Error(char* message)
{
	fprintf(stderr, "Error: %s(5s will exit)", message);
	cout<<"\n";
	Sleep(5000);
	exit(1);
}

void select(HuffmanTree HT, int n, int &s1, int &s2)
{
	s1 = 1;
	s2 = 1;
	int min  = 99999;
	int i;
	//選擇未被使用的第一個節點，
	for (i = 1; i <= n; ++i)
	{
		if (HT[i].parent == 0)
		{
			min = HT[i].weight;
			break;
		}
	}

	//find the mini s1
	for (int p =  1; p <= n; ++p)
	{
		if(0 == HT[p].parent && min >= HT[p].weight)
		{
			s1 = p;
			min = HT[p].weight;
		}
	}

	//find the s2
	min = 99999;
	for (int q =  1; q <= n; ++q)
	{
		if(0 == HT[q].parent && min >= HT[q].weight )
		{
			if( q == s1)
				continue;
			s2 = q;
			min = HT[q].weight;
		}
	}
}

5、程式碼流程