快速排序樞紐值(基元)選擇方法(轉載)
前半部分轉自:
部落格園:
後半部分轉自: 新浪部落格:供交流,無商業用途。
快速排序 Quick Sort
快速排序的基本思想是,通過一趟排序將待排記錄分割成獨立的兩部分,其中一部分記錄的關鍵字均比另一部分記錄的關鍵字小,則可分別對這兩部分記錄繼續進行排序,以達到整個序列有序。
一趟快速排序(或一次劃分)的過程如下:首先任意選取一個記錄(通常可選第一個記錄)作為樞軸(或支點)(pivot),然後按下列原則重新排列其餘記錄:將所有關鍵字比它小的記錄都安置在它的位置之前,將所有關鍵字比它大的記錄都安置在它的位置之後。
經過一趟快速排序之後,以該樞軸記錄最後所落的位置i作分界線,將序列分割成兩個子序列,之後再分別對分割所得的兩個子序列進行快速排序。
可以看出這個演算法可以遞迴實現,可以用一個函式來實現劃分,並返回分界位置。然後不斷地這麼分下去直到排序完成,可以看出函式的輸入引數需要提供序列的首尾位置。
快速排序的實現
劃分實現1 (樞軸跳來跳去法)
一趟快速排序的實現:設兩個指標low和high,設樞軸記錄的關鍵字為pivotkey,則首先從high所指位置起向前搜尋找到第一個關鍵字小於pivotkey的記錄和樞軸記錄互相交換,然後從low所指位置起向後搜尋,找到第一個關鍵字大於pivotkey的記錄和樞軸記錄互相交換,重複這兩步直至low==high為止。
下面的程式碼例子元素型別為int,並且關鍵字就是其本身。
typedef int ElemType;
int Patition(ElemType A[], int low, int high)
{
ElemType pivotkey=A[low];
ElemType temp;
while(low<high)
{
while(low <high && A[high]>=pivotkey)
{
--high;
}
temp=A[high];
A[high]=A[low];
A[low]=temp;
while(low<high && A[low]<=pivotkey)
{
++low;
}
temp=A[high];
A[high]=A[low];
A[low]=temp;
}
return low;
}
劃分實現2 (樞軸一次到位法)
從上面的實現可以看出,樞軸元素(即最開始選的“中間”元素(其實往往是拿第一個元素作為“中間”元素))在上面的實現方法中需要不斷地和其他元素交換位置,而每交換一次位置實際上需要三次賦值操作。
實際上,只有最後low=high的位置才是樞軸元素的最終位置,所以可以先將樞軸元素儲存起來,排序過程中只作元素的單向移動,直至一趟排序結束後再將樞軸元素移至正確的位置上。
程式碼如下:
Partition 實現方法2
int Patition(ElemType A[], int low, int high)
{
ElemType pivotkey=A[low];
ElemType temp = A[low];
while(low<high)
{
while(low <high && A[high]>=pivotkey)
{
--high;
}
A[low]=A[high];
while(low<high && A[low]<=pivotkey)
{
++low;
}
A[high]=A[low];
}
A[low] = temp;
return low;
}
可以看到減少了每次交換元素都要進行的三個賦值操作,變成了一個賦值操作。
細節就是每次覆蓋掉的元素都已經在上次儲存過了,所以不必擔心,而第一次覆蓋掉的元素就是樞軸元素,最後覆蓋在了它應該處於的位置。
遞迴形式的快速排序演算法
Quick Sortvoid QuickSort(ElemType A[], int low, int high)
{
if(low<high)
{
int pivotloc=Patition(A,low, high);
QuickSort(A, low, pivotloc-1);
QuickSort(A, pivotloc+1, high);
}
}
不管劃分是上面哪一種實現,都可以用這個遞迴形式進行快速排序。
需要注意的是這個if語句不能少,不然沒法停止,會導致堆疊溢位的異常。
快速排序的效能分析
時間複雜度
快速排序的平均時間為Tavg(n)=knln(n),其中n為待排序列中記錄的個數,k為某個常數,在所有同數量級的先進的排序演算法中,快速排序的常數因子k最小。
因此,就平均效能而言,快速排序是目前被認為是最好的一種內部排序方法。通常認為快速排序在平均情況下的時間複雜度為O(nlogn)。
但是,快速排序也不是完美的。
若初始記錄序列按關鍵字有序或基本有序,快速排序將蛻化為氣泡排序,其時間複雜度為O(n2)。
原因:因為每次的樞軸都選擇第一個元素,在有序的情況下,效能就蛻化了。
如下圖:
快速排序的空間利用情況
從空間上看,快速排序需要一個棧空間來實現遞迴。
若每一趟排序都將記錄序列分割成長度相接近的兩個子序列,則棧的最大深度為log2n+1(包括最外層參量進棧);但是,若每趟排序之後,樞軸位置均偏向子序列的一端,則為最壞情況,棧的最大深度為n。
如果在一趟劃分之後比較分割所得兩部分的長度,且先對長度短的子序列中的記錄進行快速排序,則棧的最大深度可降為O(logn)。
效能改善
為改進快速排序演算法,隨機選取界點或最左、最右、中間三個元素中的值處於中間的作為界點,通常可以避免原始序列有序的最壞情況。
然而,即使如此,也不能使快速排序在待排記錄序列已按關鍵字有序的情況下達到O(n)的時間複雜度(氣泡排序可以達到)。
為此,可以如下修改劃分演算法:在指標high減去1和low增加1的同時進行“起泡”操作,即在相鄰兩個記錄處於“逆序”時進行互換,同時在演算法中附設兩個布林型變數分別指示指標low和high在從兩端向中間移動的過程中是否進行過交換記錄的操作,若沒有,則不需要對低端或高階子表進行排序,這將進一步改善快速排序的平均效能。
另外,將遞迴演算法改為非遞迴演算法,也將加快速度,因為避免了進出棧和恢復斷點等工作。
改進方法:如第二篇部落格:如下:
對於分治演算法,當每次劃分時,演算法若都能分成兩個等長的子序列時,那麼分治演算法效率會達到最大。也就是說,基準的選擇是很重要的。選擇基準的方式決定了分割後兩個子序列的長度,進而對整個演算法的效率產生決定性影響。最理想的方法是,選擇的基準恰好能把待排序序列分成兩個等長的子序列。
我們介紹三種選擇基準的方法:
方法一:固定位置
取序列的第一個或最後一個元素作為基準,這是很常用的方法,但是,這也是一種很不好的處理方法。
如果輸入序列是隨機的,處理時間還是可以接受的。如果陣列已經有序時,此時的分割就是一個非常不好的分割。因為每次劃分只能使待排序序列減一,此時為最壞情況,快速排序淪為起泡排序,時間複雜度為Θ(n^2)。而且,輸入的資料是有序或部分有序的情況是相當常見的。因此,使用第一個元素作為基元是非常糟糕的。
方法二:隨機選取基準
在待排序列是部分有序時,固定選取基元會使快速排序效率低下,要緩解這種情況,就引入了隨機選取基元。這和先使序列為隨即序列,在用方法一取固定位置的元素作為基元類似。
隨機化演算法:
隨機選擇樞軸的位置,區間在low和high之間
srand((unsigned)time(NULL));
int pivotPos = rand()%(high - low) + low; //得到隨機基元的位置(下標)
這是一種相對安全的策略。由於樞軸的位置是隨機的,那麼產生的分割也不會總是會出現劣質的分割。在整個陣列數字全相等時,仍然是最壞情況,時間複雜度是O(n^2)。實際上,隨機化快速排序得到理論最壞情況的可能性僅為1/(2^n)。所以隨機化快速排序可以對於絕大多數輸入資料達到O(nlogn)的期望時間複雜度。一位前輩做出了一個精闢的總結:“隨機化快速排序可以滿足一個人一輩子的人品需求。”
方法三:三數取中(median-of-three)
雖然隨機選取基元時,減少了出現不好分割的機率,但是最壞情況下還是O(n^2),要緩解這種情況,就引入了三數取中選取基元。
最佳的劃分是將待排序的序列分成等長的子序列,最佳的狀態我們可以使用序列的中間的值,也就是第N/2個數。可是,這很難算出來,並且會明顯減慢快速排序的速度。這樣的中值的估計可以通過隨機選取三個元素並用它們的中值作為基元而得到。事實上,隨機性並沒有多大的幫助,因此一般的做法是使用左端、右端和中心位置上的三個元素的中值作為基元。
舉例:待排序序列為:8 1 4 9 6 3 5 2 7 0
左邊為:8,右邊為0,中間為6.
我們這裡取三個數排序後,中間那個數作為樞軸,則樞軸為6
注意:在選取中軸值時,可以從由左中右三個中選取擴大到五個元素中或者更多元素中選取,一般的,會有(2t+1)平均分割槽法(median-of-(2t+1),三平均分割槽法英文為median-of-three)。
對待排序序列中low、mid、high三個位置上資料進行排序,取他們中間的那個資料作為樞軸,並用0下標元素儲存樞軸。
即:採用三數取中,並用0下標元素儲存樞軸。
int SelectPivotMedianOfThree(int arr[],int low,int high)
{
int mid = low + ((high - low) >> 1);//計算陣列中間的元素的下標
//使用三數取中法選擇樞軸
if (arr[mid] > arr[high])//目標: arr[mid] <= arr[high]
{
swap(arr[mid],arr[high]);
}
if (arr[low] > arr[high])//目標: arr[low] <= arr[high]
{
swap(arr[low],arr[high]);
}
if (arr[mid] > arr[low]) //目標: arr[low] >= arr[mid]
{
swap(arr[mid],arr[low]);
}
//此時,arr[mid] <= arr[low] <= arr[high]
return arr[low];
//low的位置上儲存這三個位置中間的值
}
使用三數取中選擇樞軸優勢還是很明顯的,但是還是處理不了多數元素重複的陣列。
快速排序的二次優化:
1.使用插入排序
當待排序序列的長度分割到一定大小後,使用插入排序。
原因:對於很小和部分有序的陣列,快排不如插排好。當待排序序列的長度分割到一定大小後,繼續分割的效率比插入排序要差,此時可以使用插排而不是快排。
截止範圍的理想待排序序列長度N = 10。
if (high - low + 1 < 10)
{
InsertSort(arr,low,high);
return;
}//else時,正常執行快排
針對隨機陣列,使用三數取中選擇基元+插排,效率還是可以提高一點,但是針對已排序的陣列,是沒有任何用處的。因為待排序序列是已經有序的,那麼每次劃分只能使待排序序列減一。此時,插排是發揮不了作用的。另外,三數取中選擇基元+插排還是不能處理重複陣列。
2.聚合與基元相等的元素
在一次分割結束後,可以把與Key相等的元素聚在一起,繼續下次分割時,不用再對與key相等元素分割。
具體過程:在處理過程中,會有兩個步驟:
第一步,在劃分過程中,把與key相等元素放入陣列的兩端;
第二步,劃分結束後,把與key相等的元素移到樞軸周圍。
舉例:
待排序序列: 1 4 6 7 6 6 7 6 8 6
三數取中選取樞軸:下標為4的數6
轉換後,待分割序列:6 4 6 7 1 6 7 6 8 6 [樞軸key:6]
第一步,在劃分過程中,把與key相等元素放入陣列的兩端
結果為:6 4 1 6(樞軸) 7 8 7 6 6 6
此時,與6相等的元素全放入在兩端了
第二步,劃分結束後,把與key相等的元素移到樞軸周圍
結果為:1 4 6 6(樞軸) 6 6 6 7 8 7
此時,與6相等的元素全移到樞軸周圍了
之後,在1 4 和 7 8 7兩個子序列進行快排
如果不採用聚合基元的方法:
待排序序列:1 4 6 7 6 6 7 6 8 6
三數取中選取樞軸:下標為4的數6
轉換後,待分割序列:6 4 6 7 1 6 7 6 8 6 [樞軸key:6]
本次劃分後,未對與key元素相等處理:
結果為:1 4 6 6 7 6 7 6 8 6
下次的兩個子序列為:1 4 6 和 7 6 7 6 8 6
經過對比,我們可以看出,在一次劃分後,把與key相等的元素聚在一起,能減少迭代次數,效率會提高不少。
void QSort(int arr[],int low,int high)
{
int first = low;
int last = high;
int left = low;
int right = high;
int leftLen = 0;
int rightLen = 0;
if (high - low + 1 < 10) //插入排序
{
InsertSort(arr,low,high);
return;
}
//一次分割
int key = SelectPivotMedianOfThree(arr,low,high);//使用三數取中法選擇樞軸
while(low < high)
{
while(high > low && arr[high] >= key)
{
if (arr[high] == key)//處理相等元素
{
swap(arr[right],arr[high]);
right--;
rightLen++;
}
high--;
}
arr[low] = arr[high];
while(high > low && arr[low] <= key)
{
if (arr[low] == key)
{
swap(arr[left],arr[low]);
left++;
leftLen++;
}
low++;
}
arr[high] = arr[low];
}
arr[low] = key;
//一次快排結束
//把與樞軸key相同的元素移到樞軸最終位置周圍
int i = low - 1;
int j = first;
while(j < left && arr[i] != key)
{
swap(arr[i],arr[j]);
i--;
j++;
}
i = low + 1;
j = last;
while(j > right && arr[i] != key)
{
swap(arr[i],arr[j]);
i++;
j--;
}
QSort(arr,first,low - 1 - leftLen);
QSort(arr,low + 1 + rightLen,last);
}
在陣列中,如果有相等的元素,那麼就可以減少不少冗餘的劃分。這點在重複陣列中體現特別明顯。
3.優化遞迴操作
快排函式在函式尾部有兩次遞迴操作,我們可以對其使用尾遞迴優化。
如果待排序的序列劃分極端不平衡,遞迴的深度將趨近於n,而棧的大小是很有限的,每次遞迴呼叫都會耗費一定的棧空間,函式的引數越多,每次遞迴耗費的空間也越多。優化後,可以縮減堆疊深度,由原來的O(n)縮減為O(logn),將會提高效能。
void QSort(int arr[],int low,int high)
{
int pivotPos = -1;
if (high - low + 1 < 10)
{
InsertSort(arr,low,high); //插排
return;
}
while(low < high)
{
pivotPos = Partition(arr, low, high);
QSort(arr, low, pivot-1);
low = pivot + 1;
}
}
在第一次遞迴後,low就沒用了,此時第二次遞迴可以使用迴圈代替。
其實這種優化編譯器會自己優化,相比不使用優化的方法,差不了多少。
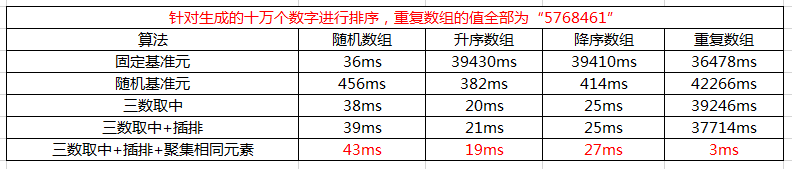
4.多種優化同時使用
這裡效率最好的快排組合是:三數取中+插排+聚集相等元素,它和STL中的Sort函式效率差不多。
都寫的非常好!!!非常感謝兩位。

