MATLAB繪製3D隱函式曲面的幾種方法
阿新 • • 發佈:2019-02-19
背景介紹
Matlab提供了一系列繪圖函式,常見的包括繪製2D曲線的plot函式、繪製2D隱函式曲線的ezplot函式、繪製3D曲面的mesh和surf函式、繪製3D顯函式曲面的ezmesh和ezsurf函式。值得注意的是,ez系列的繪圖函式裡只有ezplot是繪製隱函式曲線的,ezmesh和ezsurf都是畫顯函式曲面的(不要被ez的名字誤解了)。遺憾的是,matlab裡並沒有提供直接繪製3D隱函式曲面的函式。本帖的目的就是歸納總結幾種方便易用的繪製隱函式曲面的辦法。
問題描述
如何繪製3元方程f(x, y,z) = 0確立的隱函式曲面z = g(x,y)?其中,方程f(x, y,z) = 0
為了解決上述問題,我們需要先對幾個重要的圖形函式isosurface、patch、isonormals取得初步的瞭解,如果您已經對這三個函式很熟悉,可以直接跳過這一步。 l. isosurface 等值面函式
呼叫格式:fv = isosurface(X,Y,Z,V,isovalue) 作用:返回某個等值面(由isovalue指定)的表面(faces)和頂點(vertices)資料,存放在結構體fv中(fv由vertices、faces兩個域構成)。如果是畫隱函式 v = f(x,y,z) = 0
呼叫格式:patch(X,Y,C) 以平面座標(X, Y)為頂點,構造平面多邊形,C是RGB顏色向量 patch(X,Y,Z,C)以空間3-D座標(X, Y,Z)為頂點,構造空間3D曲面,C是RGB顏色向量 patch(fv)通過包含vertices、faces兩個域的結構體fv來構造3D曲面,fv可以直接由等值面函式isosurface得到
例如:patch(isosurface(X,Y,Z,V,0))
3. isonormals等值面法線函式
呼叫格式:isonormals(X,Y,Z,V,p) 實現功能:計算等值面V的頂點法線,將patch曲面p的法線設定為計算得到的法線(p是patch返回得到的控制代碼)。如果不設定法線的話,得到曲面在過渡地帶看起來可能不是很光滑
有了上述三個函式後,我們已經具備間接繪製3D隱函式曲面的能力了。下面以方程
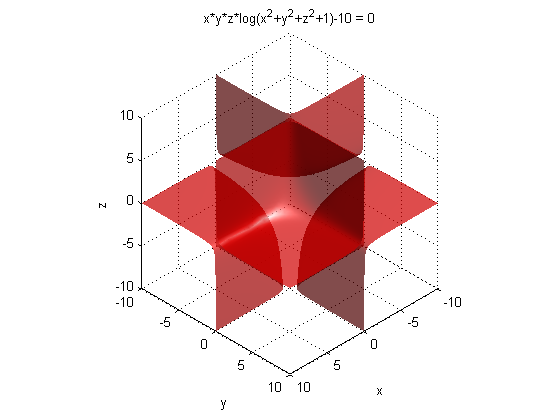
f(x,y, z) = x.*y.*z.*log(1+x.^2+y.^2+z.^2)-10 = 0為例,講解如何畫3D隱函式曲面。
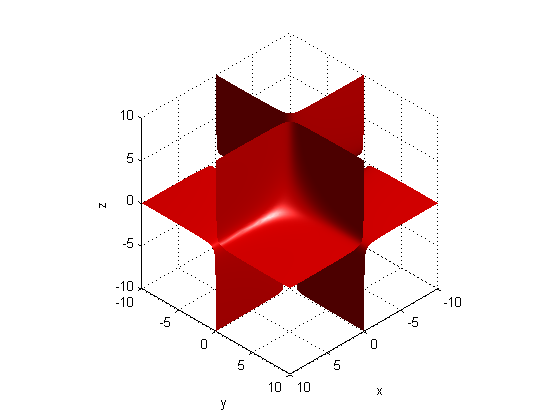
解決辦法一:isosurface + patch+ isonormals 實現原理:先定義3元顯函式v =f(x, y, z), 則 v = 0 定義的等值面就是z = g(x,y)的3D曲面。利用isosurface函式獲取v= 0 的等值面,將得到的等值面直接輸入給patch函式,得出patch控制代碼p,並畫出patch曲面的平面視角圖形。對p用isonormals函式設定曲面頂點資料的法線,最後設定顏色、亮度、3D視角,得到3D曲面。
得到圖形:
Mupad符號引擎裡提供了現成的三維隱函式畫圖函式:Implicit3d 在matlab裡開啟Mupad的方法是:在commandwindow 裡輸入mupad 來啟動一個notebook。在啟動的notebook裡再輸入如下程式碼:
若干說明:
常見問題和解決辦法:
matlab還提供一種畫切片圖形的函式slice,slice做出的圖是在切片上用顏色表示v的值。有時,我們畫切片圖形也有助於我們理解一個4維圖形。以 v= f(x,y,z) = x*y*z*exp(-(x^2+y^2+z^2)) 為例,假設我們希望看 v =f(x,y,z) 在 x =0, y = 1, z = 1 這些平面切片的圖形,我們可以用以下程式碼:
得到圖形為: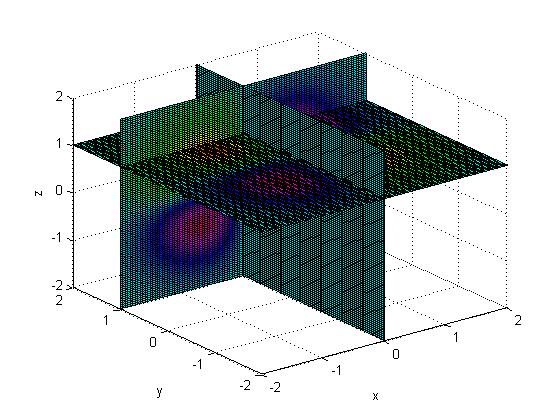
Matlab提供了一系列繪圖函式,常見的包括繪製2D曲線的plot函式、繪製2D隱函式曲線的ezplot函式、繪製3D曲面的mesh和surf函式、繪製3D顯函式曲面的ezmesh和ezsurf函式。值得注意的是,ez系列的繪圖函式裡只有ezplot是繪製隱函式曲線的,ezmesh和ezsurf都是畫顯函式曲面的(不要被ez的名字誤解了)。遺憾的是,matlab裡並沒有提供直接繪製3D隱函式曲面的函式。本帖的目的就是歸納總結幾種方便易用的繪製隱函式曲面的辦法。
問題描述
如何繪製3元方程f(x, y,z) = 0確立的隱函式曲面z = g(x,y)?其中,方程f(x, y,z) = 0
為了解決上述問題,我們需要先對幾個重要的圖形函式isosurface、patch、isonormals取得初步的瞭解,如果您已經對這三個函式很熟悉,可以直接跳過這一步。 l. isosurface 等值面函式
呼叫格式:fv = isosurface(X,Y,Z,V,isovalue) 作用:返回某個等值面(由isovalue指定)的表面(faces)和頂點(vertices)資料,存放在結構體fv中(fv由vertices、faces兩個域構成)。如果是畫隱函式 v = f(x,y,z) = 0
呼叫格式:patch(X,Y,C) 以平面座標(X, Y)為頂點,構造平面多邊形,C是RGB顏色向量 patch(X,Y,Z,C)以空間3-D座標(X, Y,Z)為頂點,構造空間3D曲面,C是RGB顏色向量 patch(fv)通過包含vertices、faces兩個域的結構體fv來構造3D曲面,fv可以直接由等值面函式isosurface得到
例如:patch(isosurface(X,Y,Z,V,0))
3. isonormals等值面法線函式
呼叫格式:isonormals(X,Y,Z,V,p) 實現功能:計算等值面V的頂點法線,將patch曲面p的法線設定為計算得到的法線(p是patch返回得到的控制代碼)。如果不設定法線的話,得到曲面在過渡地帶看起來可能不是很光滑
有了上述三個函式後,我們已經具備間接繪製3D隱函式曲面的能力了。下面以方程
f(x,y, z) = x.*y.*z.*log(1+x.^2+y.^2+z.^2)-10 = 0為例,講解如何畫3D隱函式曲面。
解決辦法一:isosurface + patch+ isonormals 實現原理:先定義3元顯函式v =f(x, y, z), 則 v = 0 定義的等值面就是z = g(x,y)的3D曲面。利用isosurface函式獲取v= 0 的等值面,將得到的等值面直接輸入給patch函式,得出patch控制代碼p,並畫出patch曲面的平面視角圖形。對p用isonormals函式設定曲面頂點資料的法線,最後設定顏色、亮度、3D視角,得到3D曲面。
程式碼如下:
f = @(x,y,z) x.*y.*z.*log(1+x.^2+y.^2+z.^2)-10; % 函式表示式
[x,y,z] = meshgrid(-10:.2:10,-10:.2:10,-10:.2:10); % 畫圖範圍
v = f(x,y,z);
h = patch(isosurface(x,y,z,v,0));
isonormals(x,y,z,v,h)
set(h,'FaceColor','r','EdgeColor','none');
xlabel('x');ylabel('y');zlabel('z');
alpha(1)
grid on; view([1,1,1]); axis equal; camlight; lighting gouraud
程式碼說明:
- alpha函式用於設定patch曲面的透明度(可以是0~1任意數值),1
表示不透明,0
表示最大透明度。如果想設定透明度為0.7,可以修改alpha(1)為alpha(0.7)。
- 使用此程式碼解決特定問題時,只需將第1行的函式表示式替換為特定問題的函式表示式,將第2行資料(x、y、z)範圍換成合適的範圍,後續程式碼無需任何變動。
得到圖形:
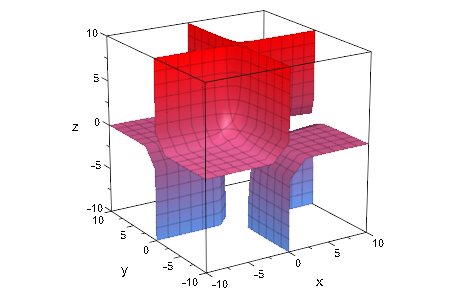
Mupad符號引擎裡提供了現成的三維隱函式畫圖函式:Implicit3d 在matlab裡開啟Mupad的方法是:在commandwindow 裡輸入mupad 來啟動一個notebook。在啟動的notebook裡再輸入如下程式碼:
plot(plot::Implicit3d(x*y*z*ln(1+x^2+y^2+z^2)-10,
x = -10..10, y = -10..10, z = -10..10), Scaling = Constrained)得到如下圖形:
解決辦法三:第三方工具包ezimplot3
- ezimplot3(f)畫函式f(X,Y,Z)= 0 在-2*pi< X < 2* pi, -2* pi < Y < 2* pi, -2* pi < Z < 2* pi上的圖形
- ezimplot3(f, [A,B])畫函式f(X,Y,Z)= 0 在A< X < B, A < Y < B, A < Z < B上的圖形
-
ezimplot3(f, [XMIN,XMAX,YMIN,YMAX,ZMIN,ZMAX])畫函式f(X,Y,Z)=
0 在XMIN< X < XMAX, YMIN < Y < YMAX, ZMIN < Z < ZMAX上的圖形
f = @(x,y,z) x*y*z*log(1+x^2+y^2+z^2)-10;
ezimplot3(f,[-10,10]); % [-10, 10] 表示圖形範圍x、y、z都在區間[-10, 10]

若干說明:
- ezimplot3和方法一本質上完全相同。即ezimplot3實際上也是基於isosurface+ patch + isonormals的實現
- ezimplot3與方法一的圖形視覺效果相同,唯一的區別是,ezimplot3的使用了0.7的透明度:alpha(0.7)
- ezimplot3在方法一基礎上增加了一些外包功能,如:允許函式控制代碼f是非向量化的函式(即函式定義無需.* ./ .^),這在ezimplot3內部會自動呼叫vectorize實現函式向量化。另外,ezimplot3可以在呼叫的時候方便的設定座標範圍。
常見問題和解決辦法:
- 常見問題:很多人在使用以上方法後,經常出現的問題是程式碼沒有任何錯誤,程式可以執行,就是出來的圖形只有一個空座標軸,看不到圖形。
- 問題分析:出現這種問題的原因是圖形的顯示區域沒設對。比如,我們上述三種方法都是在x為-10到10的範圍內,如果你設的範圍內本身就沒有圖形,那當然就看不到圖形了。
- 解決辦法:把圖形顯示範圍重新設定對即可,如果不知道圖形的大致範圍,就手工多改幾次,直到看到圖形為止
- 方法一,圖形範圍是在第2句的meshgrid函式決定的,meshgrid裡給出的x、y、z範圍就是最終畫圖範圍,修改meshgrid語句即可。
- 方法二(Mupad),x =-10..10, y = -10..10, z = -10..10是表示顯示範圍,修改這裡即可。
- 方法三,用ezimplot3(f,[A, B]) ezimplot3(f,
[XMIN,XMAX,YMIN,YMAX,ZMIN,ZMAX])兩種方式控制圖形顯示範圍。
matlab還提供一種畫切片圖形的函式slice,slice做出的圖是在切片上用顏色表示v的值。有時,我們畫切片圖形也有助於我們理解一個4維圖形。以 v= f(x,y,z) = x*y*z*exp(-(x^2+y^2+z^2)) 為例,假設我們希望看 v =f(x,y,z) 在 x =0, y = 1, z = 1 這些平面切片的圖形,我們可以用以下程式碼:
[x,y,z] = meshgrid(linspace(-2,2));
v = x.*y.*z.*exp(-(x.^2+y.^2+z.^2));
xslice = 0; yslice = 1; zslice = 1;
slice(x,y,z,v,xslice,yslice,zslice)
xlabel('x'); ylabel('y'); zlabel('z');
colormap hsv
得到圖形為: