【雙向bfs（一次也可）】【非簡單圖的最短路】UVa1599 Ideal Path 【紫書6-20經典例題】【無向圖求字典序最小的最短路】

New labyrinth attraction is open in New Lostland amusement park. The labyrinth consists of n rooms connected by m passages. Each passage is colored into some color ci. Visitors of the labyrinth are dropped from the helicopter to the room number 1 and their goal is to get to the labyrinth exit located in the room number n.

Labyrinth owners are planning to run a contest tomorrow. Several runners will be dropped to the room number 1. They will run to the room number n writing down colors of passages as they run through them. The contestant with the shortest sequence of colors is the winner of the contest. If there are several contestants with the same sequence length, the one with the ideal path is the winner. The path is the ideal path if its color sequence is the lexicographically smallest among shortest paths.

Andrew is preparing for the contest. He took a helicopter tour above New Lostland and made a picture of the labyrinth. Your task is to help him find the ideal path from the room number 1 to the room number n that would allow him to win the contest.

Note:

A sequence (a1, a2,…, ak) is lexicographically smaller than a sequence (b1, b2,…, bk) if there exists isuch that ai < bi, and aj = bj for all j < i.

Input

The input file contains several test cases, each of them as described below.

The first line of the input file contains integers n and m – the number of rooms and passages, respectively(2≤$\le$n≤$\le$100000, 1≤$\le$m≤$\le$200000). The following m lines describe passages, each passage is described with three integer numbers: ai, bi, and ci – the numbers of rooms it connects and its color (1≤$\le$ai, bi≤$\le$n, 1≤$\le$ci≤$\le$109). Each passage can be passed in either direction. Two rooms can be connected with more than one passage, there can be a passage from a room to itself. It is guaranteed that it is possible to reach the room numbern from the room number 1.

Output

For each test case, the output must follow the description below.

The first line of the output file must contain k – the length of the shortest path from the room number 1 to the room number n. The second line must contain k numbers – the colors of passages in the order they must be passed in the ideal path.

Sample Input

4 6
1 2 1
1 3 2
3 4 3
2 3 1
2 4 4
3 1 1

Sample Output

2
1 3

題意：
有n個點，m條路，每一條路都塗有顏色，要從1到n，求最短路，如果有多條，那麼選取顏色字典序最小的路，注意一條路可能連線兩個相同的點，一對點之間可能有多條路徑。保證一定有解。

TIPS：

• 結論：無需儲存父節點也能得到最短路，方法是從終點開始倒著走bfs，得到每個節點i到終點的最短距離d[i]，然後直接從起點開始走A，但是每一次到一個新的節點B時，要保證dep[B] = dep[A] - 1，這樣走過的路一定是一條最短路。

方法一：雙向BFS

思路：

• 先從終點開始走bfs，得到每一個點到終點的距離。【相當於得到一個層次圖】
• 然後從起點開始走bfs，按照上述Tips走，每次找距離減一的點走【即找下一層次的點】，選擇字典序最小的入隊，如果有多個最小顏色，將他們都入隊，並將每一層次的最小顏色記錄在陣列中，陣列的下標用層次深度記錄【層次深度為d[1] - d[i]】。走下一步時，需要考慮從這些點出發的所有點。
  

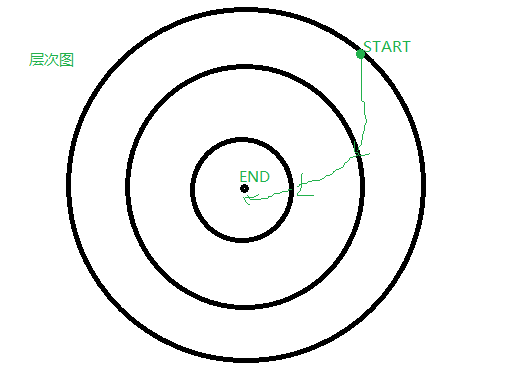
注意：

• 由於有自環和重邊的存在，因此滿足條件的一個點可能多次被加到佇列，這樣的複雜度將會成指數級。所以應該加一個vis陣列進行標記。【一定要注意細節，否則很容易TLE】
• 第一次bfs終止時機：第一次找到起點就終止，你也許會疑惑這樣是否能夠找到所有的最短路，其實是可以的，因為bfs是一層層推進的，比如最短路長為5，也就是說第五步走到起點，那麼在走第5層次之前，已經將所有深度為4的點走過了，那麼起點5一定是由這些4點走來的，那麼我們只需要從5起點往前找4點，看是哪個4點走到它的，如果有多條最短路，那麼就有這麼多個能夠走到5點的4點。
• 第二次bfs終止時機：將終點從佇列裡取出時才終止，這樣才能遍歷完所有導向終點且路徑長度一致的邊，因為把終點取出來說明最後一層次都了，要找從終點再往後走了，說明到終點的所有邊都遍歷過一遍了，這樣的結果才正確。 如果一遇到終點，還沒有把它放進去佇列前就終止，這樣只是有一條邊走向終點就結束了，並沒有考慮所有最短路。

AC程式碼：

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <string>
#include <math.h>
#include <algorithm>
#include <queue>
#define INF 0x3f3f3f3f

using namespace std;

const int maxn = 100005;
vector<int> g[maxn], w[maxn];
int n, m, vis[maxn], d[maxn], ans[maxn];

void bfs()
{
    memset(d, INF, sizeof(d));
    queue<int> q;
    q.push(n);
    d[n] = 1;
    while(!q.empty())
    {
        int cur = q.front();
        q.pop();
        int len = g[cur].size();
        for(int i = 0; i < len; i++)
        {
            int t = g[cur][i];
            if(t == 1)
            {
                d[t] = d[cur] + 1;
                printf("%d\n", d[t] - 1);
                return ;
            }
            else if(d[t] > d[cur] + 1)
            {
                d[t] = d[cur] + 1;
                q.push(t);
            }
        }
    }
}

void bfs2()
{
    memset(vis, 0, sizeof(vis));
    memset(ans, INF, sizeof(ans));
    queue<int> q;
    q.push(1);
    vis[1] = 1;
    while(!q.empty())
    {
        int minw = INF;//記錄從低層次到高其一層次的最小顏色
        int cur = q.front();
        q.pop();
        if(d[cur] == 1)
            return ;
        int len = g[cur].size();
        for(int i = 0; i < len; i++)//從某點出發找所有邊
        {
            int t = g[cur][i];
            if(d[t] == d[cur] - 1)//如果深度相差1就說明是最短路上的
                minw = min(minw, w[cur][i]);//記錄最小顏色
        }
        for(int i = 0; i < len; i++)//遍歷所有導向的點
        {
            int t = g[cur][i];
            if(d[t] == d[cur] - 1 && w[cur][i] == minw && !vis[t])//把所有在最短路上，具有最小顏色邊，且沒入隊的點入隊
            {
                q.push(t);
                vis[t] = 1;
            }
        }
        int cc = d[1] - d[cur] + 1;
        ans[cc] = min(ans[cc], minw);//記錄該層次的最小顏色，注意這裡不能直接用=，而不用‘min’，因為一個層次到高一層次的點不是一次性更新完的，需要多次出隊
    }
}

int main()
{
    while(cin >> n >> m)
    {
        for(int i = 0; i <= n; i++)
        {
            g[i].clear();
            w[i].clear();
        }
        int uu, vv, ww;
        for(int i = 0; i < m; i++)
        {
            cin >> uu >> vv >> ww;
            g[uu].push_back(vv);
            g[vv].push_back(uu);
            w[uu].push_back(ww);
            w[vv].push_back(ww);
        }
        bfs();
        bfs2();
        for(int i = 1; i < d[1]; i++)//注意輸出格式，否則WA
        {
            if(i == 1)
                printf("%d", ans[i]);
            else
                printf(" %d", ans[i]);
        }
        printf("\n");
    }
    return 0;
}

方法二：一次BFS，不斷回溯

思路：
從終點開始進行bfs,從一個點A到另外一點B這樣進行更新，如果在更新過程中，發現某一點B已經被更新過，那麼再檢查它的深度，如果dep[B] = dep[A] + 1，說明B其實是屬於A下一層次的點，而非在A前面的節點，那麼B節點儲存的資訊更優還是從A到B這樣的走法更優，就需要進行比較，再更新。那麼我們就從B點開始回溯，假設B原來的前節點是C，那麼是CB邊的顏色小一些，還是AB邊的顏色小一些，我們就進行比較，誰小就把誰的資訊儲存在B點處，如果他們倆一樣，就再往前找，找A的前節點E，C的前節點D，比較EA和DC誰的顏色小，一直這樣進行。那麼推導到起點時，每一個節點裡面都儲存的最優情況的前節點，那麼直接從起點開始回溯輸出即可。

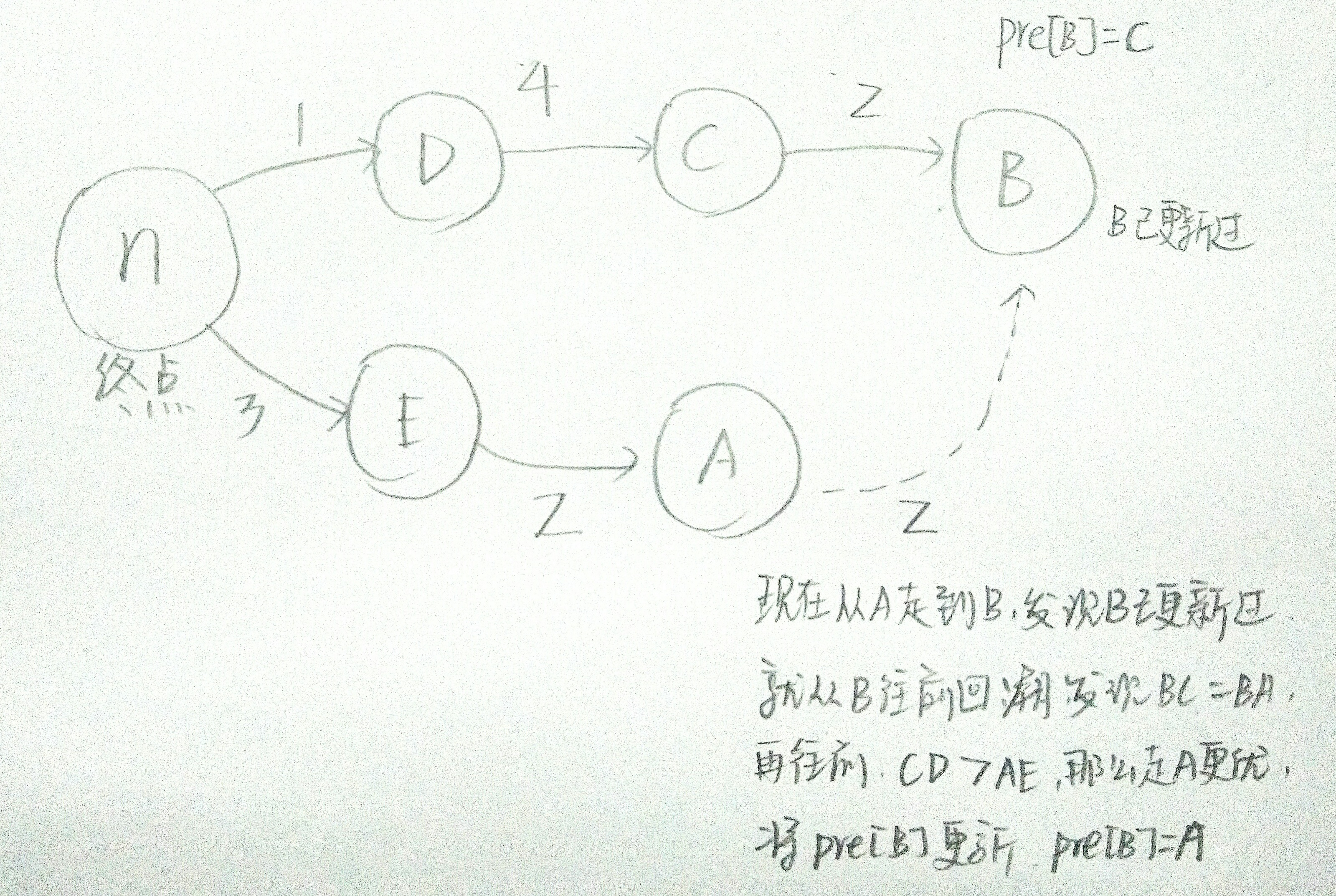
用鄰接表儲存邊和顏色時，每一個點後對應的邊的標號，和每一點可以延伸出的顏色的標號是一一對應的，因為每一次往g[v] 中加邊的同時，也向w[v]中加入了顏色。

AC程式碼：

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <string>
#include <math.h>
#include <algorithm>
#include <queue>
#define INF 0x3f3f3f3f

using namespace std;

const int maxn = 1000005;
vector<int> g[maxn], w[maxn];
int n, m, vis[maxn], d[maxn];
pair<int, int> pre[maxn];

void bfs()
{
    memset(pre, 0, sizeof(pre));
    memset(vis, 0, sizeof(vis));
    memset(d, 0, sizeof(d));
    queue<int> q;
    q.push(n);
    vis[n] = 1;
    d[n] = 1;
    pre[n] = make_pair(-1, -1);//用pair來存取某一點的前節點的標號，以及這條邊在前節點裡的位置
    while(!q.empty())
    {
        int cur = q.front();
        q.pop();
        int len = g[cur].size();
        for(int i = 0; i < len; i++)
        {
            int t = g[cur][i];
            if(vis[t])
            {
                if(d[t] == d[cur] + 1)
                {
                    pair<int, int> x = pre[t], y = make_pair(cur, i);
                    //回溯找到顏色不同的邊，注意！=-1，因為如果有兩條最短的顏色全部一樣，那麼這裡會回溯到終點，如果不停止，就會出現越界RE
                    while(x != y && x.first != -1 && y.first != -1 && w[x.first][x.second] == w[y.first][y.second])
                    {
                        x = pre[x.first];
                        y = pre[y.first];
                    }
                    if(x.first != -1 && y.first != -1 && w[x.first][x.second] > w[y.first][y.second])
                        pre[t] = make_pair(cur, i);
                }
            }
            else
            {
                vis[t] = 1;
                pre[t] = make_pair(cur, i);
                d[t] = d[cur] + 1;
                q.push(t);
            }
        }
    }
}

int main()
{
//    freopen("input.txt", "r", stdin);
//    freopen("output.txt", "w", stdout);
    while(cin >> n >> m)
    {
        for(int i = 1; i <= n; i++)
        {
            g[i].clear();
            w[i].clear();
        }
        int uu, vv, ww;
        for(int i = 0; i < m; i++)
        {
            cin >> uu >> vv >> ww;
            g[uu].push_back(vv);
            g[vv].push_back(uu);
            w[uu].push_back(ww);
            w[vv].push_back(ww);
        }
        bfs();
        printf("%d\n", d[1] - 1);
        int j;
        pair<int, int> i;
        for(i = pre[1], j = 0; i.first != -1; i = pre[i.first], j++)
        {
            if(j)
                printf(" ");
            printf("%d", w[i.first][i.second]);
        }
        printf("\n");
    }
    return 0;
}