求無向圖最小割
先解釋下名詞的意思。
無向圖的割:就是去掉一些邊,使得原圖不連通,最小割就是要去掉邊的數量最小。
解決這個問題的常用辦法就是Stoer-Wagner 演算法;
先說下這個演算法的步驟後面給出證明:
1.min=MAXINT,固定一個頂點P
2.從點P用類似prim的s演算法擴展出“最大生成樹”,記錄最後擴充套件的頂點和最後擴充套件的邊
3.計算最後擴充套件到的頂點的切割值(即與此頂點相連的所有邊權和),若比min小更新min
4.合併最後擴充套件的那條邊的兩個端點為一個頂點
5.轉到2,合併N-1次後結束
6.min即為所求,輸出min
這個演算法過程不難理解,我在這裡還是簡單的演示下演算法的過程,
任選一個點P,開始了擴充套件之路初始化wage陣列的值都是0,並且已把點P放入了已擴充套件點的集合;
第一個點P擴充套件完的wage陣列的值如下圖
(圖中邊上的權值是表示兩點間相連的邊的條數,也可以認為是兩點間的連通度)
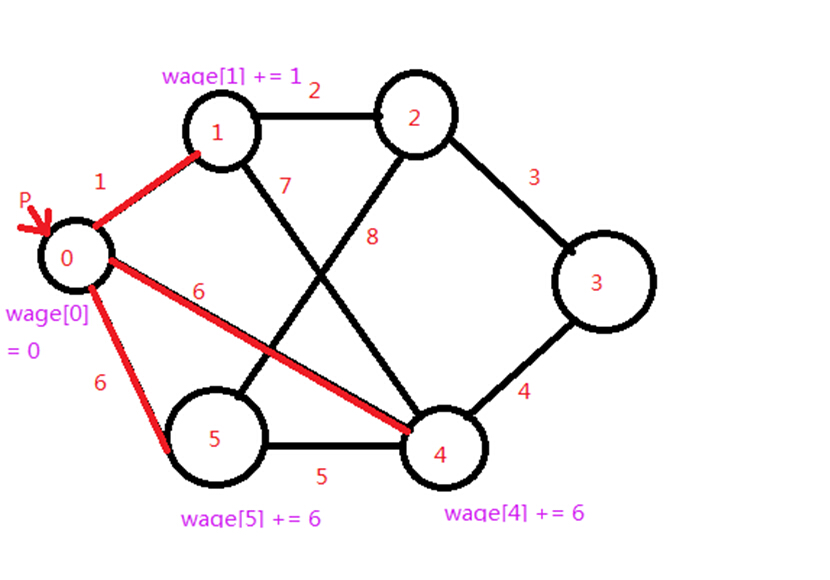
wage[4]的值最大這時候把點4加入到已訪問集合;
下一次就選取wage陣列最大值的點(也就是點4)開始向外擴充套件,注意在擴充套件點4的時候點P不會再被更新,
因為它已經進入被擴充套件集合了。過程同上。
反覆擴充套件。。。
擴充套件到最後兩個點的時候我們記為S,T;
其中T是最後一個點;
這時候我們得到了wage[S] 和 wage[T];
現在有如下性質:
1,wage[T]是將單點T分離出原圖的最小的割的值(這裡說的是把T這個點單獨拿出去);
2,wage[T]的值是將S或T單獨分離出原圖的最小割值中較小的那一個;
首先性質一很好證明,因為你最後更新到wage[T]的時候 wage[T]的值就是所有與它相連的邊的權值的和,顯然成立;
性質二的證明分為兩種情況,S與T有邊相連,和無邊相連;
S與T有邊相連時,在通過S進行擴充套件時,由於先選擇S所以擴充套件前wage[S]>=wage[T] 在擴充套件時 wage[T]的值必然會增加S與T之間的權值。
但是這個權值也是屬於S的
兩個相加了同一個數,由於之前wage[S]>=wage[T] 所以相加同一個數後不等式仍然成立;
同理S,T無邊相連也可以仿照上面的解釋;
下面要進行合點操作了,我們需要證明一件事情就是合點操作後不會影響最終的答案,
說明這個問題前,我們先進行下面的一個討論。
演算法進行到這就到了合併點的步驟了,我們先來分析下上面prim演算法的過程,
首先對於上面的性質1和性質2你要已經理解了下面的說明你才會覺得清晰。
到目前為止好像對於我們有用處的就是最後那兩個點S,T。我們不禁要問下,
如果只是為了選出兩個點,有必要這麼麻煩嗎(最大生成樹)?
直接隨意選兩個點,計算出對應的wage的值,
即計算把他們單獨分割出去的值,比較大小,小的記為T大的記為S,然後跟新min。
好像也滿足了上面所要的結果。顯然這麼做不對。我們考慮下面一種情況
我們先來想一想分割後的情況,假設我們找到了原圖的最小割然後按照最小割集進行分割,
那麼原圖一定被分為兩部分且只能是兩部分,記為A,B ;
A,B彼此連同,分割後的A,B 顯然是不連通的。
為了簡化證明過程我假設 原圖A與B 僅有一條邊相連。當然這條邊的值就是最小割的值。
這條邊連線的兩個點一個在A中一個在B中 分別記為啊a,b。
如果A中或B中只有一個點,那麼你按照隨意選點的方法不會影響最後的答案,我們這裡要討論A和B中點的個數大於1。
這時如果你還隨意的找兩個點進行更新min 合點操作就會出錯了。
這很好想,因為如果你選的是a,b 兩個點,
那麼你計算出的wage肯定是大於最小割,因為無論a,b都肯定與至少2個點相連,而最終的答案是a,b間邊的權值。
這時如果把a,b合點後再進行上面的重複操作顯然已經把最佳答案錯過了。
所以上面的這選點的prim是為了確定一個順序問題,我還以這個例子來說,
通過prim選出的兩個點S,T一定都在A中或者在B中(前提是A,B中包含2個或以上的點)
也只有在這個前提下進行點的合併才不會影響最後的答案。
我們先來證明下這兩個點一定在一邊而不會是一邊一個(前提是A,B中包含2個或以上的點)
證明:
不妨設我們prim 過程的第一個點在A中,那麼它一定先在A中的點開始擴充套件操作,
進行prim擴充套件若干次後首次計算B中點的wage 時
一定是A,B相連的那個點
此時wage[b]的值為最小割的值,接下來,
如果A中可擴充套件的點的wage值都大於wage[b],
那一定是A中的點都擴充套件玩了才會去擴充套件B中的點
那麼最後的兩個點一定都在B中。
否者,首次由b點開始擴充套件時候,
我們可以肯定的就是在A中可擴充套件的點的wage值都小於wage[b],
如果接下來B中的可擴充套件的點的wage值一直都大於A中可擴充套件點的wage值
那麼就是B中的點全都擴充套件完然後再進行A中的擴充套件最後兩個點就都在A中。
否則,在B中擴充套件若干次,再次回到A中擴充套件的時候,
B中可擴充套件點的wage值都小於A中的可擴充套件點的值,
由前面可知這個值一定小於wage[b]。
接下來就是按照這個思路,如果一直在A中那麼最後的點在B中,
如果再次回到B中擴充套件可知此時A中可擴充套件的點的wage值都小於B中可擴充套件點的wage值,反覆反覆下去,
如果最後A中一個點,B中一個點,會出現什麼情況呢?顯然最後的那個點的wage值小於wage[b]了。
這樣更新完原圖的最小割更小了,這顯然這顯然矛盾了。
矛盾的原因就在於prim的過程根本就沒法實現一個在A中一個在B中。
有了這麼個結論再討論合點不影響最後答案就很顯然了,稍微想一想畫一畫就懂了這裡就不仔細說了
如果S,T相連, 我已經更新了將S,T分割單獨分割出去時最小割的值,
那麼現在即使將S和T合併也不會影響全域性最小割的求解。
如果S,T不直接相連時,如果答案是S,T合併後的解顯然將兩者一起分離的時候已經將T單獨分開了。
肯定不會是最優的答案因為畫蛇添足啊。所以將S和T合併,並不會影響後面的計算。
到此我就粗略的說完了 無向圖最小割的演算法的正確性,以及證明,
合點操作之所以不影響答案的關鍵是prim演算法的步驟決定了選點的順序。
程式碼如下O(n^3)優化的其實效率並沒有提高。。
這個要根據題目資料決定。測試題目:廈大OJ 1100。
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
#define maxn 105
#define inf 1000000
int node[maxn],cnt[maxn],vis[maxn],p[maxn][maxn];
int main()
{
int n,m,a,b,ans=inf;
scanf("%d%d",&n,&m);
for(int i=0;i<m;i++)
{
if(i<n)
node[i]=i;
scanf("%d%d",&a,&b);
p[a][b]++;
p[b][a]++;
}
while(n>1)
{
memset(vis,0,sizeof(vis));
vis[node[0] ] =1;
int maxi = 1;
for(int i=0;i<n;i++)
{
cnt[node[i] ]=p[ node[i] ][node[0] ];
if(cnt[node[i] ]>cnt[ node[maxi] ])
{
maxi=i;
}
}
int pre = 0;
for(int s=1;s<n;s++)
{
if(s==n-1)
{
ans=min(ans,cnt[node[maxi] ]);
for(int k=0;k<n;k++)
p[node[k] ][node[pre] ] =p[node[pre] ][node [k] ] += p[node[k] ][node[maxi] ];
node[maxi] = node[--n];
}
vis[node[maxi] ] =1;
pre=maxi;
maxi=-1;
for(int i=0;i<n;i++)
{
if(!vis[node[i]])
{
cnt[node[i] ] += p[node[i] ][node[pre] ];
if(maxi==-1 || cnt[node[i] ]>cnt[node[maxi] ])
{
maxi = i;
}
}
}
}
}
printf("%d\n",ans);
return 0;
}