如果兩個連結串列無換，判斷是否相交很簡單，判斷兩個環的最後一個節點指標是否相等即可。

題目描述：上面的問題都是針對連結串列無環的，那麼如果現在，連結串列是有環的呢?上面的方法還同樣有效麼?

分析：如果有環且兩個連結串列相交，則兩個連結串列都有共同一個環，即環上的任意一個節點都存在於兩個連結串列上。因此，就可以判斷一連結串列上倆指標相遇的那個節點，在不在另一條連結串列上。

1. 無環連結串列和有環連結串列是不可能相交的;
2. 兩個有環連結串列若相交，其“整個環上”的所有node一定都重合;
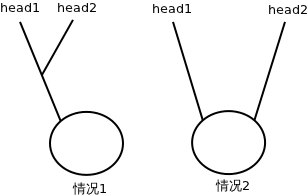
3. 有環連結串列的相交，情況只有2種：相交於”環上”或相交於”不是環的部分”,即下圖所示;

//判斷單鏈表是否存在環,引數circleNode是環內節點，後面的題目會用到
bool hasCircle(Node *head,Node *&circleNode)
{
    Node *slow,*fast;
    slow = fast = head;
    while(fast != NULL && fast->next != NULL)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(fast == slow)
        {
            circleNode = fast;
            return true;
        }
    }

    return false;
}
 

//判斷兩個帶環連結串列是否相交
bool isIntersectWithLoop(Node *h1,Node *h2)
{
    Node *circleNode1,*circleNode2;
    if(!hasCircle(h1,circleNode1))    //判斷連結串列帶不帶環，並儲存環內節點
        return false;                //不帶環，異常退出
    if(!hasCircle(h2,circleNode2))
        return false;

    Node *temp = circleNode2->next;
    while(temp != circleNode2)
    {
        if(temp == circleNode1)
            return true;
        temp = temp->next;
    }
    return false;
}