統計學習方法(2)——感知機原始形式、對偶形式及Python實現
阿新 • • 發佈:2019-02-20
感知機作為一種最簡單的線性二分類模型,可以在輸入空間(特徵空間)將例項劃分為正負兩類。本文主要介紹感知機兩種形式對應的學習演算法及Python實現。
感知機學習演算法的原始形式
對於輸入空間,感知機通過以下函式將其對映至{+1,-1}的輸出空間
對於所有的錯分類點
通過求解損失函式(2)的梯度(3),
我們很容易就可以得到感知機學習演算法的原始形式.
整個演算法流程如下:
- 選取初值w0,b0
- 在訓練集中任意選取點(xi,yi)
- 如果
−yi(w⋅xi+b)>0 則按照(4)式更新w,b - 重複2直到沒有被誤分的點
以上即為感知機演算法的原始形式,理解起來比較簡單,也較容易實現。下面給出其的Python實現
from __future__ import division
import random
import numpy as np
import matplotlib.pyplot as plt
def sign(v):
if v>=0:
return 1
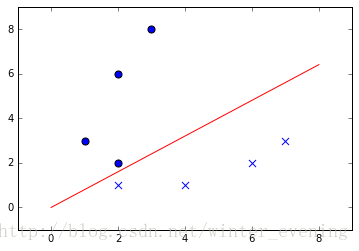
else 可以看出正負樣本被紅線分到了兩個區域。
感知機學習演算法的對偶形式
相比於原始形式,其對偶形式在理解上沒有前者那麼直觀,網上關於其實現程式碼的例子也比較少。
在《統計學習方法》一書中,關於對偶形式有如下的描述:
對偶形式的基本想法是,將w和b表示為例項
xi 和標記yi 的線性組合的形式,通過求解其係數而求得w和b.
假設w0=0,b=0,那麼從(4)式可以看出,當所有的點均不發生誤判時,最後的w,b一定有如下的形式:
(5)
其中
- 初始化
α=0 ,b=0 . - 任意選取(xi,yi)
- 如果
yi(∑j=1Nαjyjxj⋅xi+b)≤0 ,即發生誤判,則對αi,b 進行更新: