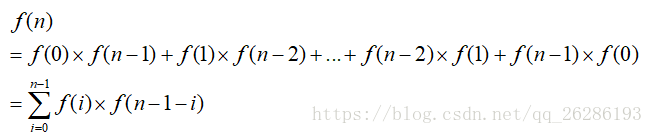【轉】【數據結構】【有n個元素依次進棧,則出棧序列有多少種】
卡特蘭數
大神解釋:https://blog.csdn.net/akenseren/article/details/82149145 權侵刪
原題
有一個容量足夠大的棧,n個元素以一定的順序入棧,出棧順序有多少種?
比如,AB兩個元素,入棧順序為AB,出棧情況有兩種:
(1)入A,出A,入B,出B,出棧順序為AB;
(2)入A,入B,出B,出A,出棧順序為BA。
因此,2個元素時,結果為2。
分析:設f(n)為“n個元素以一定的順序入棧,出棧順序的種類數”。顯然f(1)=1,f(2)=2。我們現在來分析一般情況。一般情況下,我們可以按照“第一個入棧的元素,在出棧序列中的位置”作為分類手段。
舉個例子,我們假設入棧元素為A,B,C,D。我們按照“A在出棧序列中的位置”分類討論:
(1)當A第一個出棧時,A先進,然後馬上出棧。這種情況下,共有“BCD出棧順序的種類數”種方案。也就是f(n-1)。
(2)當A第二個出棧時,A先進,B再進,之後B需要馬上出來(這樣才能確保A排第二)。此時共有f(n-2)種方案。
(3)當A第三個出棧時,A先進,之後只要確保排在A後面兩個的元素比A先出即可。此時共有f(2)*f(n-3)種方案。f(2)是指“BC入棧出棧順序的種類數”,f(n-3)是指”D入棧出棧的種類數”。
……
分析到這裏,規律就很顯然了。
從第一項開始,分別是第一個入棧元素在第i+1個出棧的情況數。
上式中,令f(0)=1 。
這個實際上是卡特蘭數(Catalan number,又稱卡塔蘭數)。
若編程實現,需要維護一個一維數組,時間復雜度為O(n^2)。(遞歸實現的時間復雜度太高)。
卡塔蘭數的通項公式為h(n)=C(2n,n)-C(2n,n+1)(n=0,1,2,...)。
元素A、B、C、D依次進棧,寫出所有可能的出棧序列
應該有14種情況
A第一個出棧:ABCD;ACBD;ACDB;ABDC;ADCB;
A第二個出棧:BACD;BADC;
A第三個出棧:CBAD;BCAD;
A第四個出棧:BCDA;CBDA;CDBA;BDCA;DCBA.
卡特蘭數
卡特蘭數前幾項為 : 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...
令h(0)=1,h(1)=1,catalan數滿足遞推式: h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0) (n>=2)
例如:h(2)=h(0)*h(1)+h(1)*h(0)=1*1+1*1=2
h(3)=h(0)*h(2)+h(1)*h(1)+h(2)*h(0)=1*2+1*1+2*1=5
另類遞推式: h(n)=h(n-1)*(4*n-2)/(n+1);
遞推關系的解為: h(n)=C(2n,n)/(n+1) (n=1,2,3,...)
遞推關系的另類解為: h(n)=c(2n,n)-c(2n,n+1)(n=1,2,3,...)
本題目的常規分析
首先,我們設f(n)=序列個數為n的出棧序列種數。同時,我們假定第一個出棧的序數是k。
第一個出棧的序數k將1~n的序列分成兩個序列,其中一個是1~k-1,序列個數為k-1,另外一個是k+1~n,序列個數是n-k。
此時,我們若把k視為確定一個序數,那麽根據乘法原理,f(n)的問題就等價於——序列個數為k-1的出棧序列種數乘以序列個數為n - k的出棧序列種數,即選擇k這個序數的f(n)=f(k-1)×f(n-k)。而k可以選1到n,所以再根據加法原理,將k取不同值的序列種數相加,得到的總序列種數為:f(n)=f(0)f(n-1)+f(1)f(n-2)+……+f(n-1)f(0)。
看到此處,再看看卡特蘭數的遞推式,答案不言而喻,即為f(n)=h(n)= C(2n,n)/(n+1)= c(2n,n)-c(2n,n+1)(n=1,2,3,……)。
最後,令f(0)=1,f(1)=1。
非常規分析
問題等價於:n個1和n個0組成一2n位的2進制數,要求從左到右掃描,1的累計數不小於0的累計數,試求滿足這條件的數有多少?【對於每一個數來說,必須進棧一次、出棧一次。我們把進棧設為狀態‘1’,出棧設為狀態‘0’】
解答: 設P2n為這樣所得的數的個數。在2n位上填入n個1的方案數為 C(n 2n)
不填1的其余n位自動填以數0。從C(n 2n)中減去不符合要求的方案數即為所求。
不合要求的數指的是從左而右掃描,出現0的累計數超過1的累計數的數。
不合要求的數的特征是從左而右掃描時,必然在某一奇數2m+1位上首先出現m+1個的累計數,和m個1的累計數。
此後的2(n-m)-1位上有n-m個1,n-m-1個0。如若把後面這部分2(n-m)-1位,0與1交換【就是0換成1 1換成0 不是順序的調換 是數值換】,使之成為n-m個0,n-m-1個1,結果得 1個由n+1個0和n-1個1組成的2n位數,即一個不合要求的數對應於一個由n-1個0和n+1個1組成的一個排列。
類似問題 買票找零
1.有2n個人排成一行進入劇場。入場費5元。其中只有n個人有一張5元鈔票,另外n人只有10元鈔票,劇院無其它鈔票,問有多少中方法使得只要有10元的人買票,售票處就有5元的鈔票找零?(將持5元者到達視作將5元入棧,持10元者到達視作使棧中某5元出棧)
最終結果:C(2n,n)-C(2n,n+1)
2.
* * * * * * * * * * * * * * * 形如這樣的直角三角形網格,從左上角開始,只能向右走和向下走,問總共有多少種走法? 問題的由來:編號為 1 到 n 的 n 個元素,順序的進入一個棧,則可能的出棧序列有多少種? 對問題的轉化與思考:n 個元素進棧和出棧,總共要經歷 n 次進棧和 n 次出棧。這就相當於對這 2n 步操作進行排列。 一個模型:一個 n*n 的正方形網格,從左上角頂點到右下角頂點,只能向右走和向下走。問共有多少種走法。如果將向右走對應上述問題的出棧,向下走對應上述問題的進棧,那麽,可 以視此模型為對上述問題的具體描述。而解決此問題,只要在總共從左上角到右下角的2n步中,選定向右走的步數,即共有C(n 2n)種走法。 但是存在一個問題,如果走法越過了對角線,那麽對應到上述問題是出棧數比入棧數多,這是不符合實際的。 對以上模型進行處理,對角線將以上正方形網格分成兩部分,只留下包含對角線在內的下半部分,那麽就不會出現越過對角線的問題。而這問題就是開始提出的問題。 3.在圓上選擇2n個點,將這些點成對連接起來使得所得到的n條線段不相交的方法數? https://blog.csdn.net/hackbuteer1/article/details/7450250 沒懂【轉】【數據結構】【有n個元素依次進棧,則出棧序列有多少種】