PM、GAN、InfoGAN、對抗自編碼模型對比
本文源自知乎，僅作為個人學習使用。
作者：鄭華濱鏈接：https://zhuanlan.zhihu.com/p/27159510
來源：知乎
著作權歸作者所有。商業轉載請聯系作者獲得授權，非商業轉載請註明出處。
前段時間我受極視角邀請，在鬥魚上直播分享有關GAN的話題。考慮到現在網上關於GAN的文章、視頻都已經非常多了，所以我就故意選擇了一個之前沒有什麽人講過的主題：LSTM之父Schmidhuber與GAN之間的恩怨糾葛。其實這件事在英文網上傳播得還挺廣，而且除了八卦之外也有一些嚴肅的學術討論，可惜相關的中文信息寥寥，不過這樣倒正好給我一個機會來給大家介紹一些新內容。
其實相比視頻直播我還是更喜歡寫成文章的形式，因為後者更適合深入理解和收藏回顧。所以為了方便錯過直播或者不習慣看視頻的朋友，我對當晚直播內容進行了文字整理，全文分為以下四個部分：
- 八卦Schmidhuber與GAN之間的恩怨
- 講解Schmidhuber在92年提出的PM模型
- 簡單介紹GAN、InfoGAN、對抗自編碼器三個模型
- 對比以上四個模型之間的異同
如果選擇看直播回放，可以到百度雲下載。
鏈接：http://pan.baidu.com/s/1skUZidn
密碼：200j
一、雙雄捉對
2016年12月，NIPS大會，Ian Goodfellow的GAN Tutorial上，發生了尷尬的一幕。
正當Goodfellow講到GAN與其他模型的比較時，臺下一位神秘人物站起來打斷了演講，自顧自地說了一大通話（視頻片段在此）
這個觀眾不是別人，卻是大名鼎鼎的Jürgen Schmidhuber，一位來自德國的AI科學家。雖然名聲不如三巨頭響亮，但Schmidhuber其實也是深度學習的先驅人物，在上個世紀就做出了許多重要貢獻，其中最有名的就是他在1997年提出的LSTM，而他本人也被尊稱為”LSTM之父”。
本文八卦的正是這位大佬跟Goodfellow在GAN上的爭論，但其實這早就不是Schmidhuber第一次開炮懟人了。再往前2015年的時候，我們熟知的三巨頭Hinton、Lecun、Bengio在Nature上發表了一篇《Deep Learning》綜述之後，Schmidhuber就站出來指責他們行文偏頗，認為他們沒有重視自己做出的很多貢獻，覺得自己沒有得到應有的榮譽，而Lecun之後也發文霸氣反駁，場面十分激烈。當然這不是本文的重點，感興趣的朋友可以進一步挖掘，下面還是繼續回到NIPS演講現場，看看Schmidhuber這回究竟又是為何開炮。
只見他站起來之後，先講自己在1992年提出了一個叫做Predictability Minimization的模型，它如何如何，一個網絡幹嘛另一個網絡幹嘛，花了好幾分鐘，接著話鋒一轉，直問臺上的Goodfellow：“你覺得我這個PM模型跟你的GAN有沒有什麽相似之處啊？”
似乎只是一個很正常的問題，可是Goodfellow聽完後反應卻很激烈。Goodfellow表示，Schmidhuber已經不是第一次問我這個問題了，之前呢我和他就已經通過郵件私下交鋒了幾回，所以現在的情況純粹就是要來跟我公開當面對質，順便浪費現場幾百號人聽tutorial的時間。然後你問我PM模型和GAN模型有什麽相似之處，我早就公開回應過你了，不在別的地方，就在我當年的論文中，而且後來的郵件也已經把我的意思說得很清楚了，還有什麽可問的呢？
確實正如Goodfellow所言，早在2014年的第一篇GAN論文中，PM已經被拿出來跟GAN進行了比較，舉了三點不同之處。不過那只是論文的最終版本，而在一開始投遞NIPS的初稿中並沒有下面這段文字，也就是說很可能Goodfellow一開始是不知道有PM這麽一個東西的。
那為什麽在最終版本裏又出現了PM的內容呢？原來，當年Schmidhuber就是NIPS的審稿人，而且剛好就審到了Goodfellow的論文。我們現在知道這篇論文挖了一個巨大無比的坑，引得大批人馬前仆後繼都來做GAN的研究，以後也應該是能寫進教科書的經典工作。但就是這樣牛逼的一篇論文，當年Schmidhuber居然給出了拒稿意見！當然另外兩位審稿人識貨，所以論文最後還是被收了。
回到正題，當時Schmidhuber在評審意見中認為，他92年提出的PM模型才是“第一個對抗網絡”，而GAN跟PM的主要差別僅僅在於方向反過來了，可以把GAN名字改成“inverse PM”，即反過來的PM。按他的意思，GAN簡直就是個PM的變種模型罷了。
Goodfellow當然不同意，所以就有了14年最終版本裏的三點不同之處，具體細節放在最後模型比較的部分再講。然而Schmidhuber並不接受這些說法，私下裏又通過郵件跟Goodfellow進行了一番爭論，還到16年的NIPS大會上打斷演講，公開較勁，就是想讓對方承認PM模型的地位和貢獻，可謂不依不饒。
Goodfellow也不客氣，幹脆在2016年的GAN Tutorial中完全移除了對PM的比較和引用。他在Quora上公開表示，“我從沒有否認GAN跟另外一些模型有聯系，比如NCE，但是GAN跟PM之間我真的認為沒太大聯系。”更有意思的是，Goodfellow還透露說，“Jürgen和我準備合寫一篇paper來比較PM和GAN——如果我們能夠取得一致意見的話。”想必真要寫出來，背後又要經過一番激烈的爭論了。
說了這麽多，所謂的PM模型究竟是什麽？它跟GAN究竟有多少相同多少不同？還有，這個“古老”的模型能給今天的GAN研究帶來什麽啟發嗎？大家心裏肯定充滿了疑問。那麽八卦結束，我們現在就來走近科學，走近塵封多年的PM模型。
二、古老智慧
Predictability Minimization（可預測性最小化）模型，簡稱PM模型，出自1992年的論文《Learning Factorial Codes by Predictability Minimization》，Jürgen Schmidhuber是唯一的作者。對於類似我這樣二零一幾年才接觸深度學習的人來說，它幾乎就是“中古時期”的文獻了。
理解PM模型，首先得從自編碼器說起。大家知道機器學習分為有監督學習、無監督學習和強化學習，無監督學習中一個很重要的領域是表征學習，旨在從原始數據中學習到一個良好的表征，而自編碼器就是用於表征學習的代表模型。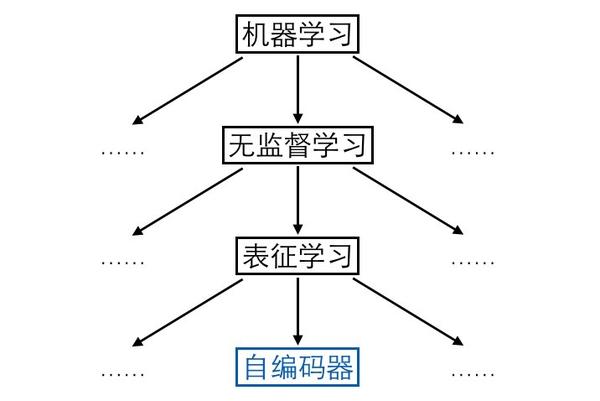
自編碼器由兩個模塊——編碼器（encoder）和解碼器（decoder）組成。編碼器負責輸入原始樣本，輸出壓縮編碼（code）；解碼器負責輸入編碼，還原出原始樣本。解碼還原出來的樣本跟真正的原始樣本進行比較，可以計算重構誤差，自編碼器的訓練目標就是盡可能地減少這個重構誤差。
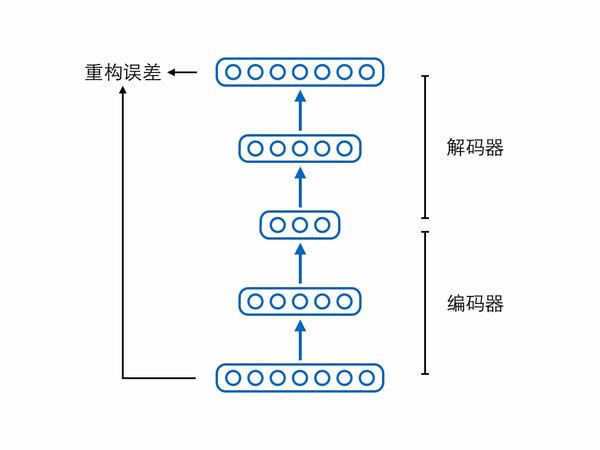如果自編碼器經過訓練能夠很好地重構樣本，那意味著編碼器和解碼器中間的隱藏層節點保留了原始樣本的重要信息，我們把中間這層節點構成的向量稱為表征（representation）、特征（feature）或編碼（code），這三個詞其實可以當成同義詞。
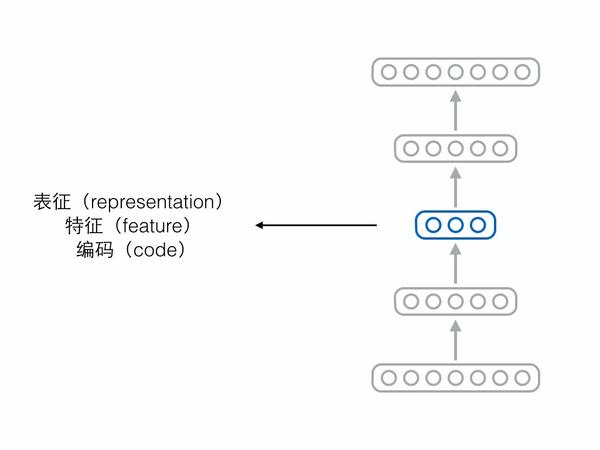但是僅僅保留樣本信息、僅僅學到一個表征，是不夠的，因為表征學習的一大難點就是想要學到一個“好”的表征。但什麽是“好”呢？有很多人提出了不同的標準。
比如有人認為編碼向量的各個維度代表了樣本所具有的屬性，而單獨一個樣本不應該同時具備那麽多種屬性，所以合理的情況是編碼向量中大多數維度都是0（不激活），只有少數維度不為0（激活），此為“稀疏”，附帶稀疏要求的編碼器就叫稀疏自編碼器。
再比如有人認為自編碼器不能死記硬背，需要在“理解”樣本的基礎上對樣本進行編碼，即便輸入的時候存在一些噪聲損壞了樣本，自編碼器也要能夠還原出完好的原始樣本，在此條件下編碼出來的向量可能會更具語義信息，此為“降噪”，附帶降噪要求的編碼器就叫降噪自編碼器。
除了稀疏、降噪，還有人認為編碼向量的各個維度之間應該相互獨立，此為“解耦”（factorial / disentangled），也是下文的重點。為了方便起見，我們考慮編碼只有3個維度的情況，此時解耦在數學形式上表現為：
（1）
其中是全部訓練樣本而非單個樣本，
對應編碼的第
個維度。為方便起見，下文省略
。
直觀上說，一個解耦的編碼（factorial code）把原本混雜在樣本中的各個獨立要素拆解開來，用一個個維度分別表示，就像人類通過拆解獨立要素來認知復雜事物一樣，所以可以認為它是一個“好”的表征。
現在問題來了，我們可以通過L1正則化給來自編碼器提出稀疏的要求，可以通過輸入加噪來給自編碼器提出降噪的要求，那要怎麽給自編碼器提出解耦的要求呢？當年Schmidhuber就想到了非常聰明的方法。
首先，上面公式（1）可以換一個表述，改寫成三個條件獨立表達式：
（2a）
（2b）
（2c）
直觀上可以把這組式子解釋為，一個編碼維度旁邊的“兄弟維度”對於預測該維度沒有額外幫助，比如說知道了和
並不能幫助我們將
猜得更準。
接著，使用三個預測器網絡把上述邏輯具體化，其中預測器1負責預測維度1，輸入維度2和3，以此類推，數學形式如下：
（3a）
（3b）
網絡形式如下：
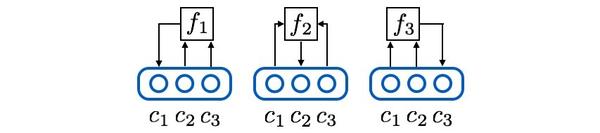為了讓預測器猜準它所負責的編碼維度，可以把它的loss函數定為L2 loss（或者其他預測誤差loss）：
（4a）
（4b）
（4c）
按Schmidhuber的思想，上述loss體現了各個編碼維度的解耦程度。怎麽說呢？以預測器1為例，如果和
很有關系，甚至極端情況下
恒等於
，那麽
就能夠猜得很準。此時
關於
條件不獨立，很有可預測性（predictability），我們就認為
沒能從
中解耦。
這顯然不是想要的局面。為了將與
解耦，編碼器就得盡可能讓預測器猜不中，loss上體現為：
（5）
預測器1想要猜中維度1，而編碼器想要讓它猜不中，loss函數剛好相反，，兩者之間存在對抗。如果編碼器贏了，就代表與
關系不大，成功解耦。
接下來考慮上所有維度，再把公式寫得通用一點。每個預測器試圖猜中它所負責的編碼維度，體現了編碼的可預測性，其loss為：
（6）
編碼器試圖讓所有預測器都猜不中，試圖最小化可預測性，其loss與預測器相反：
（7）
如果編碼器贏了，就解耦了編碼向量的各個維度。至此，讀者就可以理解Schmidhuber論文標題的含義了：Learning Factorial Codes by Predictability Minimization，通過最小化可預測性，來學習一個解耦的編碼表示。
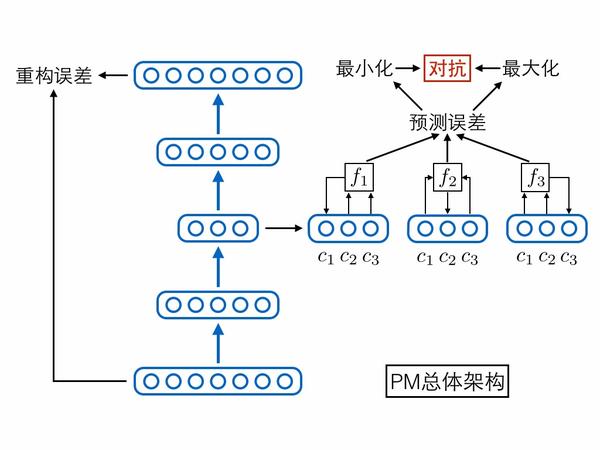
當然，除了上述兩個相互對抗可預測性loss，別忘了還有個自編碼器本身的重構誤差loss，它能夠保證編碼中盡可能保留了原始輸入樣本的重要信息。論文中其實還有其他loss，但不是重點，感興趣的人可以去讀原論文。將上述網絡模塊與loss函數全部集中在一起，就形成了PM模型的總體架構圖，我們用這張圖作為第二部分的總結：
三、三個後輩
知道了PM是啥，接下來的問題就是它跟GAN究竟有多相似，但實際上GAN的兩個後續變種——InfoGAN、對抗自編碼器反而跟PM更像，所以第三部分先簡單介紹這三個模型，再在第四部分跟PM進行綜合比較。相關論文如下：
Generative Adversarial NetsInfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets
Adversarial Autoencoders
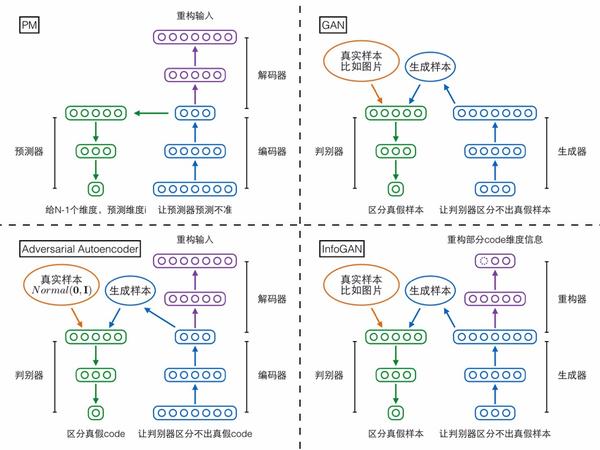
第一個模型是大家已經很熟悉的GAN，分為生成器（generator）和判別器（discriminator）兩個模塊。生成器輸入一個隨機編碼向量，輸出一個復雜樣本（如圖片）；判別器輸入一個復雜樣本，輸出一個概率表示該樣本是真實樣本還是生成器產生的假樣本。判別器的目標是區分真假樣本，生成器的目標是讓判別器區分不出真假樣本，兩者目標相反，存在對抗。
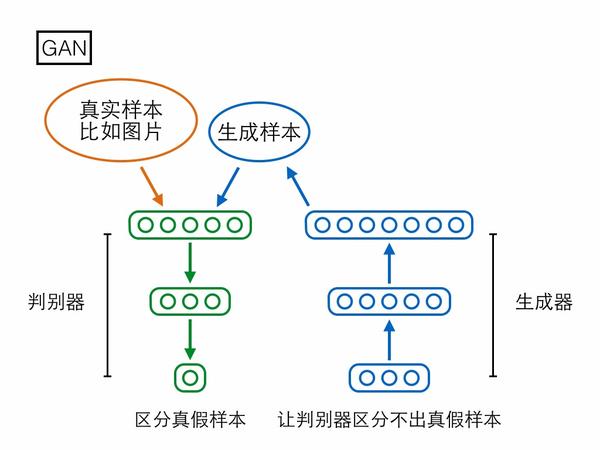GAN的生成器輸入一個100維的編碼向量，但在生成樣本的過程中未必會用上全部維度，可能有些維度提供了絕大部分重要信息，另外一些維度只是陪襯，提供一些無關痛癢的隨機擾動。然而究竟哪些維度編碼了重要信息，哪些維度僅僅提供隨機擾動？在GAN的架構下我們既沒法知道，也沒法控制。
第二個模型InfoGAN卻可以做到。先來看它的結構，相比GAN多了個重構器模塊，用於重構生成器輸入的隨機編碼向量，但是只重構由我們指定的一部分維度。
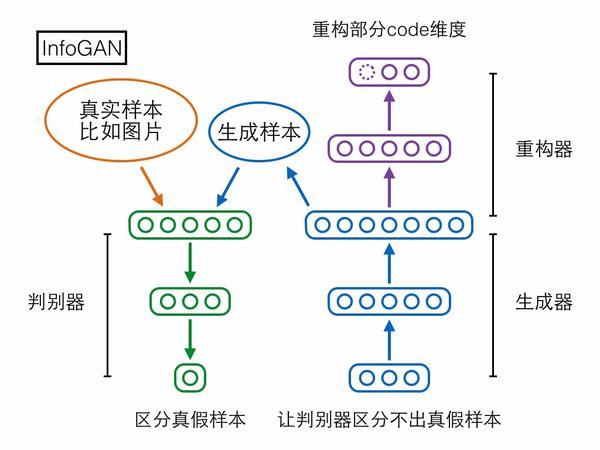加上重構器模塊之後，如果生成器拿這一部分維度當成無關痛癢的隨機擾動來用，那重構器的任務就會比較艱難；但如果生成器拿這一部分維度當成樣本的重要信息（或者套用PCA的術語，主成分）來用，那麽輸出樣本就會和這部分編碼維度高度相關，此時重構器能夠比較輕松地從樣本重構出原來的這部分編碼。兩相對比，生成器就會傾向於使用我們指定的這一部分維度來作為樣本的重要信息（主成分）。訓練結束後，甚至有機會觀察到有些維度具有非常顯著的語義信息，比如InfoGAN論文在MNIST手寫數字上訓練之後，可以觀察到某個維度完全控制著0-9的數字類別，某個維度完全控制著數字圖像從左到右的傾斜程度，這些顯然就是MNIST數據集的重要信息（主成分）：
對於已經讀過InfoGAN論文的人，我需要補充解釋一下，上述講法跟論文的講法不太一樣。論文是從互信息的角度開始推導，經過一些變分推斷的技巧最終得到模型的loss，但其實最終得到的loss基本上就是普通的重構誤差。對於離散維度，論文最終推出的loss是log likelihood，一般對離散維度設置的重構誤差也是如此；對於連續維度，論文最終推出的loss是對多維高斯分布取log，如果簡化高斯分布中的協方差矩陣是單位矩陣，該loss就等價於普通的L2 loss，也是一般對連續維度設置的重構誤差形式。
無論是GAN、InfoGAN還是其他GAN變種，基本上都想學習從零均值、一方差的標準高斯分布到復雜樣本分布的映射，而GAN的思路是先固定前者（標準高斯分布）作為網絡輸入，再慢慢調整網絡輸出去匹配後者（復雜樣本分布）。
第三個模型Adversarial Autoencoder（對抗自編碼器）卻采取了相反的思路！它是先固定後者（復雜樣本分布）作為網絡輸入，再慢慢調整網絡輸出去匹配前者（標準高斯分布）。具體來說，對抗自編碼器包含三個模塊——編碼器、解碼器、判別器，前兩者構成一個普通的自編碼器，輸入的復雜樣本，還是要求在解碼器的輸出端重構；判別器輸入編碼向量，判定它是來自一個真實的標準高斯分布，還是來自編碼器的輸出。判別器試圖區分編碼向量的真假，編碼器就試圖讓判別器區分不出真假，如果最終編碼器贏了，就意味著它輸出的編碼很接近標準高斯分布，導致判別器混淆不清，我們的目的也就達到了。對抗自編碼器嚴格來說應該不算GAN的變種，因為它的思路方向與GAN相反。
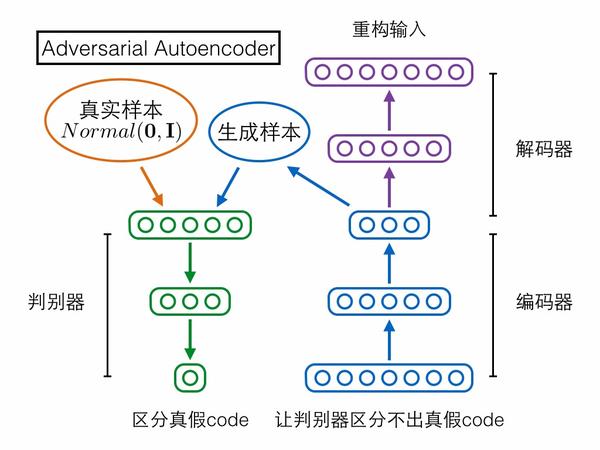說到跟GAN方向相反，讀者可能會記起上文提到Schmidhuber把GAN叫做“inverse PM”。PM跟GAN相反，對抗自編碼器也和GAN相反，那它們兩個會不會很像呢？答案是確實很像，如果把PM的架構圖參照上面三個模型重新畫一遍，就可以很清晰地看到PM跟對抗自編碼器的主體架構完全對的上。
需要註意的是，上圖其實把N個預測器合並畫成了一個。
最後，一圖總結第三部分：
四、縱橫融匯
最後是對上述四個模型做綜合比較。首先對比PM和GAN：
1.映射方向相反
- PM的編碼器把復雜分布映射為解耦分布
- PM的解碼器把解耦分布映射為復雜分布
- GAN的生成器把一個解耦的高斯分布映射為復雜分布
其中PM的編碼器和GAN的生成器方向相反，所以Schmidhuber把GAN稱為“inverse PM”。
2.都是對抗優化相反的目標
- PM的預測器要猜準某一維編碼，編碼器要讓它猜不準
- GAN的判別器要區分真假樣本，生成器要讓它區分不準
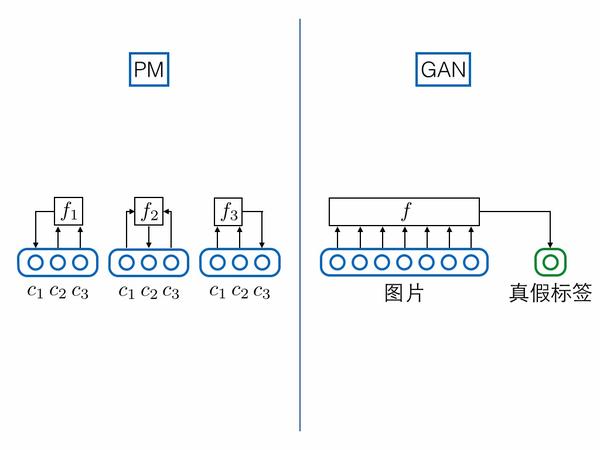
3.預測/判別結構相似
如果把真假標簽的節點跟圖片樣本節點拼接到一起，視為一個超長向量的話，GAN的判別器就可以強行視為PM預測器的特例：PM對每一個維度都要預測，但是GAN只預測真假標簽這一特殊維度。
4.模型主體不同（Goodfellow在GAN論文中提出）
- PM的主體是自編碼重構，對抗訓練僅僅作為一個正則，起到輔助作用
- GAN的主體就是對抗訓練，沒有其他目標
5.可拓展性不同
- PM的思想最多只能做到把編碼建模為解耦分布，沒辦法施加其他要求，施加其他要求那就不是PM的功勞了
- GAN雖然具體把編碼建模為解耦高斯分布，但其實對編碼的分布並沒有任何限制，完全可以直接換成其他分布來建模，無論是均勻分布還是別的什麽分布都沒問題，甚至可以用另一個復雜分布比如圖片來作為編碼，讓生成器輸入一張圖片輸出另一張圖片，可拓展性非常強大。
Goodfellow在GAN論文中還提了其他不同點，但是我個人覺得不合理，就忽略不講了。經過上述比較，我們可以看到PM和GAN確實有非常多的相似之處，但是差異也很大，我個人覺得並不能把GAN簡單看作PM的變種。
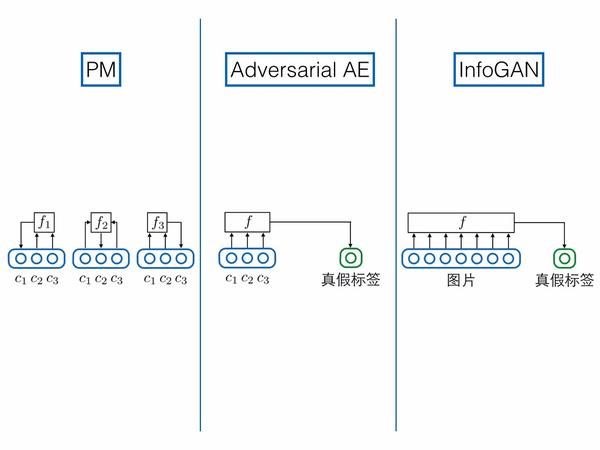
相比之下，PM和InfoGAN、對抗自編碼器反倒更像：
1.模型主體
- PM主體是自編碼器，要求重構復雜分布的樣本
- 對抗自編碼器主體是自編碼器，要求重構復雜分布的樣本
- InfoGAN主體可以視為自編碼器，要求重構（部分）編碼向量
2.對網絡中間層的要求
- PM要求編碼器和解碼器中間的隱藏層解耦，它是通過可預測性最小化的思想來做到的
- 對抗自編碼器要求編碼器和解碼器中間的隱藏層解耦，且滿足高斯分布，它是通過對抗訓練，拉近隱藏層編碼分布與一個真正的解耦高斯分布來做到的
- InfoGAN要求生成器和重構器中間的隱藏層滿足復雜樣本分布，它是通過對抗訓練，拉近生成分布與真實復雜分布來做到的
3.預測/判別結構相似
PM輸入編碼其他維度，預測某一維度；對抗自編碼器，輸入編碼全部維度，預測真假標簽；InfoGAN和前面GAN的情況相同，輸入圖片，預測真假標簽。在這個角度上對抗自編碼器與PM更相似。
四個模型對比完畢，我們能夠獲得什麽啟發嗎？下面試舉一例，來結束第四部分。
inference.vc是一個關於生成模型的著名博客，其中有篇文章認為對抗自編碼器中用GAN來拉近編碼分布和高斯分布，是殺雞用牛刀的做法。
文章認為，GAN模型強大的分布拉近能力適用於圖片這樣的復雜分布，但是對於像解耦高斯分布如此簡單的情況，並不需要動用到GAN這種大殺器，其實完全可以利用解耦高斯分布的特殊形式，采取更加高效的方式（比如文章中提了一個叫做MMD的方法，此處略過不講）。
看了PM之後就可以想到另一個思路——分別要求解耦和高斯。先把對抗自編碼器的判別器換成PM模型的N組預測器，用可預測性最小化的思想，實現編碼向量各個維度之間的解耦；接著對每個單獨的編碼維度，通過GAN使其滿足高斯分布。雖然還是用GAN，但是我們把向量上的對抗訓練轉化為標量上的對抗訓練，而後者可能比前者要容易和穩定得多。
五、總結
Schmidhuber在92年提出的PM模型通過可預測性最小化來學習一個解耦的編碼表示，編碼器和預測器優化相反的目標，確實是比GAN更早地使用了對抗訓練的思想。
PM不僅跟GAN，還跟InfoGAN、對抗自編碼器存在很多相似之處，但還是有很明顯的差異。其中PM和對抗自編碼器最像，主體都是自編碼器，但它們並不能簡單地視為GAN的變種。
我們現在都是盯著最新最前沿的研究工作，其實也許有很多像PM這樣“古老”但有趣的想法被我們忽視了，有的是因為當年提出的時候思想太過超前，或者硬件計算能力撐不起來，導致無人問津，最典型的例子就是LSTM。這些工作不應該被埋沒，如果能夠重新挖掘出來的話，就可能給今天的研究帶來很多新的啟發。
PM、GAN、InfoGAN、對抗自編碼模型對比