一個 names nload coin getc bbf continue cif 通過

C. Five Dimensional Points time limit per test 2 seconds memory limit per test 256 megabytes input standard input output standard output

You are given set of n points in 5-dimensional space. The points are labeled from 1 to n. No two points coincide.

We will call point a bad if there are different points b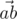

and c, not equal to a, from the given set such that angle between vectors and 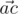is acute (i.e. strictly less than 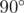). Otherwise, the point is called good.

The angle between vectors 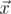and 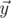in 5-dimensional space is defined as 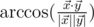, where 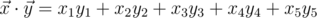is the scalar product and 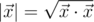is length of .

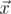Given the list of points, print the indices of the good points in ascending order.

Input

The first line of input contains a single integer n (1 ≤ n ≤ 103) — the number of points.

The next n lines of input contain five integers ai, bi, ci, di, ei (|ai|, |bi|, |ci|, |di|, |ei| ≤ 103) — the coordinates of the i-th point. All points are distinct.

Output

First, print a single integer k — the number of good points.

Then, print k integers, each on their own line — the indices of the good points in ascending order.

Examples input Copy

6
0 0 0 0 0
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1

output Copy

1
1

input Copy

3
0 0 1 2 0
0 0 9 2 0
0 0 5 9 0

output Copy

0

Note

In the first sample, the first point forms exactly a 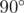angle with all other pairs of points, so it is good.

In the second sample, along the cd plane, we can see the points look as follows:

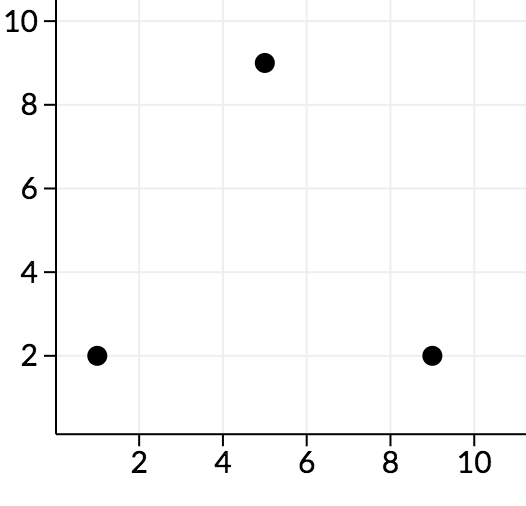
We can see that all angles here are acute, so no points are good.

題意：

給你n個五維空間上的n個點。

讓你求出“好”的點的數量。

“好”的點的定義是：

對於一個點i，不存在任何其他兩個點，j,k， （三個點互不相同） 使得向量 i->j和向量 i - > k 是銳角。

思路：

判斷兩個向量的夾角是否是銳角可以通過向量的點積來判斷。

五維空間的點積和二維三維的都一樣，都是對應坐標相乘再相加。

然後每一次點積後的結果都可以得出這樣的結論。

如圖，如果點積後的結果小於等於零，那麽證明∠J I K不是銳角。

那麽就得出結論 j 和k都不是good點，因為對於j，有i和k是的所成的角是銳角。

k同理。

而如果點積結果大於0，那麽證明 角jik是銳角，所以i不是good point

需要一個數組vis來維護哪些點是已經被確定不是good點的，以此來降低時間復雜度。

註意到枚舉的時候，第三個變量k，設為j+1開始枚舉，這樣不會讓i，j，k每一次重復計算而導致答案錯誤。

細節見代碼：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define rt return
#define dll(x) scanf("%I64d",&x)
#define xll(x) printf("%I64d\n",x)
#define sz(a) int(a.size())
#define all(a) a.begin(), a.end()
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), ‘\0‘, sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define db(x) cout<<"== [ "<<x<<" ] =="<<endl;
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
ll lcm(ll a,ll b){return a/gcd(a,b)*b;}
ll powmod(ll a,ll b,ll MOD){ll ans=1;while(b){if(b%2)ans=ans*a%MOD;a=a*a%MOD;b/=2;}return ans;}
inline void getInt(int* p);
const int maxn=1010;
const int inf=0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
int vis[maxn];
struct node
{
    ll a,b,c,d,e;
}arr[maxn];
int n;
ll f(int i,int j,int k)
{
    ll a1=arr[j].a-arr[i].a;
    ll a2=arr[k].a-arr[i].a;
    ll b1=arr[j].b-arr[i].b;
    ll b2=arr[k].b-arr[i].b;
    ll c1=arr[j].c-arr[i].c;
    ll c2=arr[k].c-arr[i].c;
    ll d1=arr[j].d-arr[i].d;
    ll d2=arr[k].d-arr[i].d;
    ll e1=arr[j].e-arr[i].e;
    ll e2=arr[k].e-arr[i].e;
    ll res=a1*a2+b1*b2+c1*c2+d1*d2+e1*e2;
    return res;
}
int main()
{
    //freopen("D:\\common_text\\code_stream\\in.txt","r",stdin);
    //freopen("D:\\common_text\\code_stream\\out.txt","w",stdout);

    gbtb;
    cin>>n;
    repd(i,1,n)
    {
        cin>>arr[i].a>>arr[i].b>>arr[i].c>>arr[i].d>>arr[i].e;
    }
    repd(i,1,n)
    {
        if(i==2)
        {
            i=2;
        }
        if(vis[i])
            continue;
        repd(j,1,n)
        {
            if(i==j)
            {
                continue;
            }
            repd(k,j+1,n)
            {
                if(k==j||k==i)
                {
                    continue;
                }
                if(f(i,j,k)<=0)
                {
                    vis[j]=vis[k]=1;
                    break;
                }else
                {
                    vis[i]=1;
                    break;
                }
            }
            if(vis[i])
                break;
        }
    }
    int ans=0;
    repd(i,1,n)
    {
        if(!vis[i])
        {
            ans++;
        }
    }
    cout<<ans<<endl;
    repd(i,1,n)
    {
        if(!vis[i])
        {
            cout<<i<<" ";
        }
    }cout<<endl;
    return 0;
}

inline void getInt(int* p) {
    char ch;
    do {
        ch = getchar();
    } while (ch == ‘ ‘ || ch == ‘\n‘);
    if (ch == ‘-‘) {
        *p = -(getchar() - ‘0‘);
        while ((ch = getchar()) >= ‘0‘ && ch <= ‘9‘) {
            *p = *p * 10 - ch + ‘0‘;
        }
    }
    else {
        *p = ch - ‘0‘;
        while ((ch = getchar()) >= ‘0‘ && ch <= ‘9‘) {
            *p = *p * 10 + ch - ‘0‘;
        }
    }
}

Five Dimensional Points CodeForces - 851C （計算幾何+暴力）