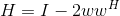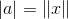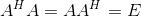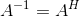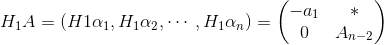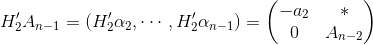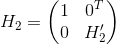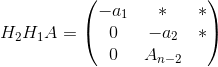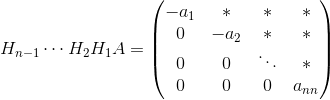Math-Model(五)正交分解(QR分解)
正交分解
矩陣的正交分解又稱為QR分解,是將矩陣分解為一個正交矩陣Q和一個上三角矩陣的乘積的形式。
任意實數方陣A,都能被分解為 。這裡的Q為正交單位陣,即 R是一個上三角矩陣。這種分解被稱為QR分解。 QR分解也有若干種演算法,常見的包括Gram–Schmidt、Householder和Givens演算法。 QR分解是將矩陣分解為一個正交矩陣與上三角矩陣的乘積。用一張圖可以形象地表示QR分解: 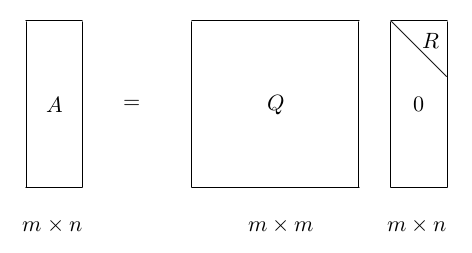
為啥我們需要正交分解呢?
實際運用過程中,QR分解經常被用來解線性最小二乘問題,這個問題我們後面講述。
提到正交分解就不得不討論(Householder transformation Householder變換)豪斯霍爾德變換和(Schmidt orthogonalization Schmidt正交化)施密特正交化
Schmidt正交化
定理1 設A是n階實非奇異矩陣,則存在正交矩陣Q和實非奇異上三角矩陣R使A有QR分解;且除去相差一個對角元素的絕對值(模)全等於1的對角矩陣因子外,分解是唯一的.
定理2 設A是m×n實矩陣,且其n個列向量線性無關,則A有分解A=QR,其中Q是m×n實矩陣,且滿足QHTQ=E,R是n階實非奇異上三角矩陣該分解除去相差一個對角元素的絕對值(模)全等於1的對角矩陣因子外是唯一的.用Schmidt正交化分解方法對矩陣進行QR分解時,所論矩陣必須是列滿秩矩陣。
演算法步驟
- 寫出矩陣的列向量;
- 列向量按照Schmidt正交化正交;
- 得出矩陣的Q′,R′;
- 對R′的列向量單位化得到Q,R′的每行乘R′每列的模得푹
matlab程式碼
function[X,Q,R] = QRSchmidt(A,b) %方陣的QR的Gram-Schmidt正交化分解法,並用於求解AX=b方程組[m,n]=size(A); if m~=n %如果不是方陣,則不滿足QR分解要求 disp('不滿足QR分解要求'); end Q=zeros(m,n); X=zeros(n,1); R=zeros(n); for k=1:nR(k,k)=norm(A(:,k)); if R(k,k)==0 break; end Q(:,k)=A(:,k)/R(k,k); for j=k+1:n R(k,j)=Q(:,k)'*A(:,j); A(:,j)=A(:,j)-R(k,j)*Q(:,k); end if nargin==2 b=Q'* b; X(n)=b(n)/R(n,n); for i=n-1:-1:1 X(i)=(b(i)-sum(R(i,i+1:n).*X(i+1:n)'))/R(i,i); end else X=[]; end end
Householder變換
設A為任一n階方陣,則必存在n階酉矩陣Q和n階上三角陣R,使得A=QR
設w∈Cn是一個單位向量,令
則稱H是一個Householder矩陣或Householder變換。則對於任意的存在Householder矩陣H,使得Hx=-au。其中
酉矩陣(unitary matrix)
若n階復矩陣A滿足
則稱A為酉矩陣,記之為其中,Ah是A的共軛轉置
酉矩陣性質
如果A是酉矩陣
也是酉矩陣;
- det(A)=1;
- 充分條件是它的n個列向量是兩兩正交的單位向量。
演算法步驟
- 將矩陣A按列分塊寫成A=(α1,α2,...,αn).如果α1≠0,則可得,存在n階householder矩陣H1使得
於是有
如果α1=0,則直接進行下一步,此時相當於取,而a1=0.
- 將矩陣An-1按列分塊寫成An-1=(αi,α2,... ,αn-1)。如果α1≠0,則可得,存在n-1階householder矩陣H’2使得
於是有
此時,令
則H2是n階Householder矩陣,且使
如果α1=0,則直接進行下一步- 對n-2階矩陣繼續進行類似的變換,如此下去,之多在第n-1步,我們可以找到Householder矩陣H1,H2,...,Hn-1使得
令,則Q是酉矩陣之積,從而必有酉矩陣並且A=QR
matlab程式碼
function[ X,Q,R ] = QRHouseholder(A,b)
%用Householder變換將方陣A分解為正交Q與上三角矩陣R的乘積,並用於求解AX=b方程組
[n,n]=size(A);
E=eye(n);
X=zeros(n,1);
R=zeros(n);
P1=E;
for k=1:n-1
%構造w,使Pk=I-2ww'
s=-sign(A(k,k))* norm(A(k:n,k));
R(k,k)=-s;
if k==1
w=[A(1,1)+s,A(2:n,k)']';
else
w=[zeros(1,k-1),A(k,k)+s,A(k+1:n,k)']';
R(1:k-1,k)=A(1:k-1,k);
end
if norm(w)~=0
w=w/norm(w);
end
P=E-2*w*w';
A=P*A;
P1=P*P1;
R(1:n,n)=A(1:n,n);
end
Q=P1';
if nargin==2
b=P1*b;
X(n)=b(n)/R(n,n);
for i=n-1:-1:1
X(i)=(b(i)-sum(R(i,i+1:n).*X(i+1:n)'))/R(i,i);
end
else
X=[];
end
matlab自帶方法
%產生一個3*3大小的魔方矩陣
A=magic(3)
[Q,R]=qr(A)
使用Eigen C++ Eigen提供了幾種矩陣分解的方法
| 分解方式 | Method | 矩陣滿足條件 | 計算速度 | 計算精度 |
|---|---|---|---|---|
| PartialPivLU | partialPivLu() | Invertible | ++ | + |
| FullPivLU | fullPivLu() | None | - | +++ |
| HouseholderQR | householderQr() | None | ++ | + |
| ColPivHouseholderQR | colPivHouseholderQr() | None | + | ++ |
| FullPivHouseholderQR | fullPivHouseholderQr() | None | - | +++ |
| LLT | llt() | Positive definite | +++ | + |
| LDLT | ldlt() | Positive or negative semidefinite | +++ | ++ |
其中HouseholderQR、ColPivHouseholderQR、FullPivHouseholderQR是我們目前要用到的QR分解方法
C++的QR分解程式碼為
#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
using namespace std;
int main() {
Matrix3d A;
A<<1,1,1,
2,-1,-1,
2,-4,5;
HouseholderQR<Matrix3d> qr;
qr.compute(A);
MatrixXd R = qr.matrixQR().triangularView<Upper>();
MatrixXd Q = qr.householderQ();
std::cout << "QR2(): HouseholderQR---------------------------------------------"<< std::endl;
std::cout << "A "<< std::endl <<A << std::endl << std::endl;
std::cout <<"qr.matrixQR()"<< std::endl << qr.matrixQR() << std::endl << std::endl;
std::cout << "R"<< std::endl <<R << std::endl << std::endl;
std::cout << "Q "<< std::endl <<Q << std::endl << std::endl;
std::cout <<"Q*R" << std::endl <<Q*R << std::endl << std::endl;
return 0;
}
輸出
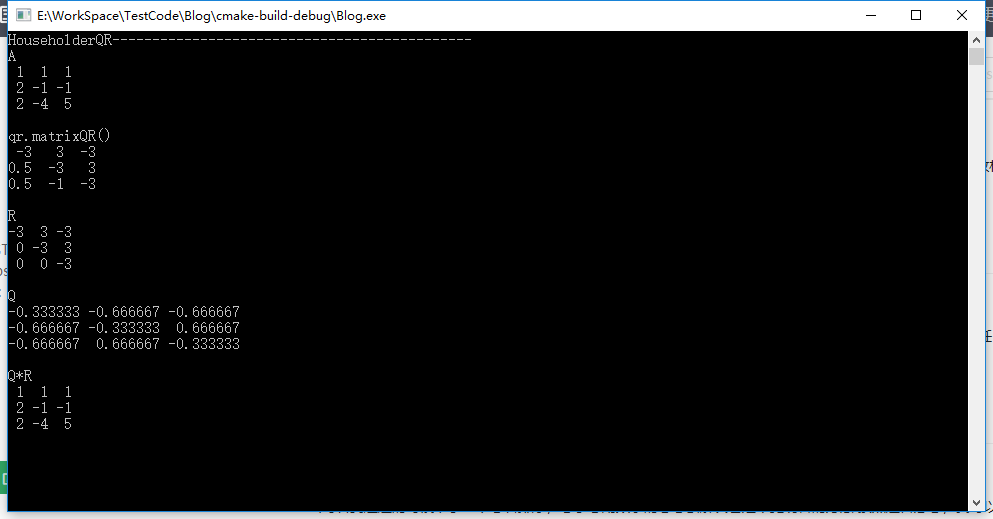
好了大功告成,為什麼我要寫計算方法的文章呢,雖然現在有很多的庫和包給我們呼叫,但是我們也不能忘了程式碼的本質是為了解決複雜的數學問題,從根源上去理解一種計算方法有助於我們對自身程式碼的優化,比如這些方法我們可以把它寫到FPGA和CUDA等並行或者分散式的計算當中,加速我們的計算方法,這比直接單機去呼叫這些庫會