poj 1179 Polygon (區間dp)
阿新 • • 發佈:2019-05-01
urn stand pick 最大值 sym step == layer range
On the first move, one of the edges is removed. Subsequent moves involve the following steps:
?replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2.
The game ends when there are no more edges, and its score is the label of the single vertex remaining.
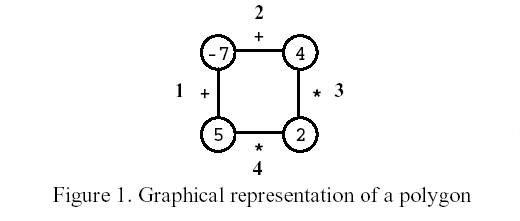
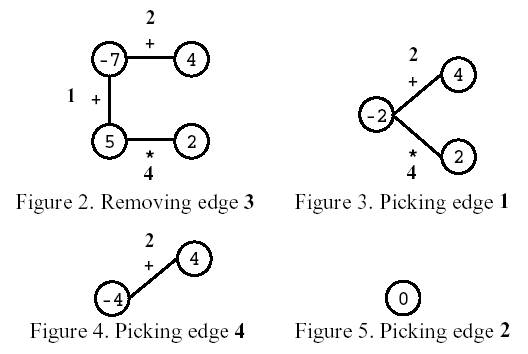
Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0.
Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score.
3 <= N <= 50
For any sequence of moves, vertex labels are in the range [-32768,32767].
Description
Polygon is a game for one player that starts on a polygon with N vertices, like the one in Figure 1, where N=4. Each vertex is labelled with an integer and each edge is labelled with either the symbol + (addition) or the symbol * (product). The edges are numbered from 1 to N.
On the first move, one of the edges is removed. Subsequent moves involve the following steps:
?replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2.
The game ends when there are no more edges, and its score is the label of the single vertex remaining.
Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0.

Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score.
Input
3 <= N <= 50
For any sequence of moves, vertex labels are in the range [-32768,32767].
Output
Your program is to write to standard output. On the first line your program must write the highest score one can get for the input polygon. On the second line it must write the list of all edges that, if removed on the first move, can lead to a game with that score. Edges must be written in increasing order, separated by one space.Sample Input
4
t -7 t 4 x 2 x 5
Sample Output
33
1 2
題意:已知一個環形的圓 有n個點和n條邊 現在讓你任意去掉一條邊 然後每次根據邊的符號合並兩個點 要求合並成1個點的最大值
思路:和石子合並很像 我們只需要把鏈擴大為原來的兩倍在這個長度上dp就行了 值得註意的是 最大值可能由兩個最小值相乘得到 所以我們既要維護最大值同時也要記錄最小值
在這個思路上區間dp即可
#include<cstdio> #include<cstring> #include<algorithm> #include<iostream> #include<string> #include<vector> #include<stack> #include<bitset> #include<cstdlib> #include<cmath> #include<set> #include<list> #include<deque> #include<map> #include<queue> #define ll long long int using namespace std; inline ll gcd(ll a,ll b){return b?gcd(b,a%b):a;} inline ll lcm(ll a,ll b){return a/gcd(a,b)*b;} int moth[13]={0,31,28,31,30,31,30,31,31,30,31,30,31}; int dir[4][2]={1,0 ,0,1 ,-1,0 ,0,-1}; int dirs[8][2]={1,0 ,0,1 ,-1,0 ,0,-1, -1,-1 ,-1,1 ,1,-1 ,1,1}; const int inf=0x3f3f3f3f; const ll mod=1e9+7; int dp[107][107][2]; char op[107]; int a[107]; int arry[107]; int main(){ ios::sync_with_stdio(false); int n; while(cin>>n){ for(int i=1;i<=n;i++){ cin>>op[i]>>a[i]; a[i+n]=a[i]; op[i+n]=op[i]; //兩倍長鏈 } for(int i=1;i<=2*n;i++) //初始化邊界 for(int j=1;j<=2*n;j++) dp[i][j][1]=inf,dp[i][j][0]=-inf; for(int i=1;i<=2*n;i++){ dp[i][i][0]=dp[i][i][1]=a[i]; //處理邊界 } for(int len=2;len<=n;len++) //長度 for(int i=1;i+len<=2*n;i++){ //起點 int j=i+len-1; for(int k=i;k<j;k++){ //分割點 if(op[k+1]==‘t‘){ dp[i][j][0]=max(dp[i][j][0],dp[i][k][0]+dp[k+1][j][0]); dp[i][j][1]=min(dp[i][j][1],dp[i][k][1]+dp[k+1][j][1]); }else{ dp[i][j][0]=max(dp[i][j][0], max(dp[i][k][1]*dp[k+1][j][1],dp[i][k][0]*dp[k+1][j][0])); dp[i][j][1]=min(dp[i][j][1], min(dp[i][k][1]*dp[k+1][j][0], min(dp[i][k][1]*dp[k+1][j][1],dp[i][k][0]*dp[k+1][j][1]))); } } } int ans=-inf; int sz=0; for(int i=1;i<=n;i++){ if(ans<dp[i][i+n-1][0]){ ans=dp[i][i+n-1][0]; sz=1; arry[sz]=i; }else if(ans==dp[i][i+n-1][0]){ arry[++sz]=i; } } cout<<ans<<endl; for(int i=1;i<=sz;i++){ if(i==1) cout<<arry[i]; else cout<<" "<<arry[i]; } cout<<endl; } return 0; }
poj 1179 Polygon (區間dp)
