題意

Description

XX在進行字符串研究的時候，遇到了一個十分棘手的問題。

在這個問題中，給定一個字符串S，與一個整數K，定義S的子串T=S(i, j)是關於第K位的識別子串，滿足以下兩個條件：

1、i≤K≤j。

2、子串T只在S中出現過一次。

例如，S="banana"，K=5，則關於第K位的識別子串有"nana"，"anan"，"anana"

現在，給定S，XX希望知道對於S的每一位，最短的識別子串長度是多少，請你來幫助他。

Input

僅一行，輸入長度為N的字符串S。

Output

輸出N行，每行一個整數，第i行的整數表示對於第i位的最短識別子串長度。

Sample Input

Sample Output

HINT

N<=5*10^5

Source

分析

參照jklover的題解。

SAM + 線段樹.

先建出 parent 樹,按照題意,我們只需要處理 right 集合大小為 1 的節點.
如下圖,先算出這樣的一個節點合法長度的 max,min ( min 可以用 max(fa)+1 計算).

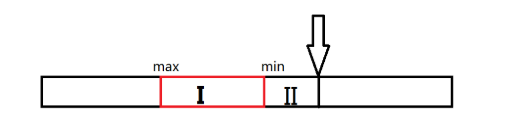
那麽區域 I 內每個點的貢獻就是區域 II 的長度加上這個點到區域 II 的距離.
區域 II 內每個點的貢獻就是區間 II 的長度.開兩顆線段樹分別修改就可以了.

如何維護區域1呢？考慮他的答案是pos[u]-i+1，直接更新pos[u]，那麽把最終線段樹上的值-i就是答案了。這種操作比較常見。

時間復雜度\(O(n \log n)\)

代碼

#include<bits/stdc++.h>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
    rg T data=0,w=1;rg char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') w=-1;ch=getchar();}
    while(isdigit(ch)) data=data*10+ch-'0',ch=getchar();
    return data*w;
}
template<class T>il T read(rg T&x) {return x=read<T>();}
typedef long long ll;
using namespace std;

co int N=2e5,INF=0x3f3f3f3f;
struct node{int min,tag;};
#define lc (x<<1)
#define rc (x<<1|1)
struct SegTree{
    node t[N*4];
    void pushup(int x){
        t[x].min=min(t[lc].min,t[rc].min);
    }
    void modify(int x,int v){
        t[x].min=min(t[x].min,v),t[x].tag=min(t[x].tag,v);
    }
    void pushdown(int x){
        if(t[x].tag<INF){
            modify(lc,t[x].tag),modify(rc,t[x].tag);
            t[x].tag=INF;
        }
    }
    void build(int x,int l,int r){
        t[x].min=t[x].tag=INF;
        if(l==r) return;
        int mid=l+r>>1;
        build(lc,l,mid),build(rc,mid+1,r);
    }
    void update(int x,int l,int r,int ql,int qr,int v){
        if(ql<=l&&r<=qr) return modify(x,v);
        pushdown(x);
        int mid=l+r>>1;
        if(ql<=mid) update(lc,l,mid,ql,qr,v);
        if(qr>mid) update(rc,mid+1,r,ql,qr,v);
        pushup(x);
    }
}T1,T2;
int ans[N];
void query(int x,int l,int r){
    if(l==r) return ans[l]=min(T1.t[x].min-l,T2.t[x].min),void();
    T1.pushdown(x),T2.pushdown(x);
    int mid=l+r>>1;
    query(lc,l,mid),query(rc,mid+1,r);
}
// SAM
char buf[N];
int n,tot=1,last=1;
int ch[N][26],fa[N],len[N],pos[N],siz[N];
void extend(int c,int po){
    int p=last,cur=last=++tot;
    len[cur]=len[p]+1,pos[cur]=po,siz[cur]=1;
    for(;p&&!ch[p][c];p=fa[p]) ch[p][c]=cur;
    if(!p) fa[cur]=1;
    else{
        int q=ch[p][c];
        if(len[q]==len[p]+1) fa[cur]=q;
        else{
            int clone=++tot;
            memcpy(ch[clone],ch[q],sizeof ch[q]);
            fa[clone]=fa[q],len[clone]=len[p]+1,pos[clone]=pos[q];
            fa[q]=fa[cur]=clone;
            for(;ch[p][c]==q;p=fa[p]) ch[p][c]=clone;
        }
    }
}
int cnt[N],ord[N];
int main(){
    scanf("%s",buf+1),n=strlen(buf+1);
    for(int i=1;i<=n;++i) extend(buf[i]-'a',i);
    for(int i=1;i<=tot;++i) ++cnt[len[i]];
    for(int i=1;i<=n;++i) cnt[i]+=cnt[i-1];
    for(int i=1;i<=tot;++i) ord[cnt[len[i]]--]=i;
    T1.build(1,1,n),T2.build(1,1,n);
    for(int i=tot;i>=1;--i){
        int u=ord[i];
        siz[fa[u]]+=siz[u];
        if(u==1||siz[u]>1) continue;
        int l=pos[u]-len[u]+1,r=pos[u]-len[fa[u]];
        if(l<=r-1) T1.update(1,1,n,l,r-1,pos[u]+1);
        T2.update(1,1,n,r,pos[u],len[fa[u]]+1);
    }
    query(1,1,n);
    for(int i=1;i<=n;++i) printf("%d\n",ans[i]);
    return 0;
}

BZOJ1396 識別子串 和 BZOJ2865 字符串識別