前文連結

【動態規劃】01揹包問題

【動態規劃】01揹包問題【續】

【動態規劃】完全揹包問題

【動態規劃】多重揹包問題

說明

看完前面四篇關於揹包問題的文章，你會發現揹包問題其實也不過如此，而且它們之間有很多相似的地方，本篇文章就來揭開它們面紗，將揹包問題徹底搞定。

三種揹包問題的比較

先來回顧一下三個揹包問題的定義：

01揹包：
有N件物品和一個容量為V的揹包，第i件物品消耗的容量為Ci，價值為Wi，求解放入哪些物品可以使得揹包中總價值最大。

完全揹包：
有N種物品和一個容量為V的揹包，每種物品都有無限件可用，第i件物品消耗的容量為Ci，價值為Wi，求解放入哪些物品可以使得揹包中總價值最大。

多重揹包：
有N種物品和一個容量為V的揹包，第i種物品最多有Mi件可用，每件物品消耗的容量為Ci，價值為Wi，求解入哪些物品可以使得揹包中總價值最大。

三種揹包問題都有一個共同的限制，那就是揹包容量，揹包的容量是有限的，這便限制了物品的選擇，而三種揹包問題的共同目的，便是讓揹包中的物品價值最大。

不同的地方在於物品數量的限制，01揹包問題中，每種物品只有一個，對於每種物品而言，便只有選和不選兩個選擇。完全揹包問題中，每種物品有無限多個，所以可選的範圍要大很多。在多重揹包問題中，每種物品都有各自的數量限制。

三種揹包問題雖然對於物品數量的限制不一樣，但都可以轉化為01揹包問題來進行思考。在完全揹包問題中，雖然每種物品都可以選擇無限個，但由於揹包容量有限，實際上每種物品可以選擇的數量也是有限的，那麼將每種物品都看做是 V/Ci 種只有一件的不同物品，不就成了01揹包問題嗎？對於多重揹包也是如此，只是每種物品的膨脹數量變成了 min{Mi, V/Ci}。

所以說，01揹包問題是所有揹包問題的基礎，弄懂了01揹包問題後，完全揹包和多重揹包就沒有什麼難的地方了。

下面我們來對比一下三種揹包問題的狀態轉移方程，以便更好的理解它們之間的聯絡：

01揹包的狀態轉移方程：

F[i,v] = max{F[i-1,v], F[i-1,v-Ci] + Wi}

完全揹包的狀態轉移方程：

F[i,v] = max{F[i-1,v-kCi] + kWi | 0 <= kCi <= v}

多重揹包的狀態轉移方程：

F[i,v] = max{F[i-1,v-kCi] + kWi | 0 <= k <= Mi}

把這三個方程放到一起，便能很清晰的看到它們之間的關係了，三種揹包問題都是基於子問題來選取價值最大的一個，只是選擇的範圍不一樣。

01揹包考慮的是選和不選，所有隻需要比較兩種策略的最大值即可，而完全揹包和多重揹包要考慮的是選幾個的問題。

這樣說也許還是不夠形象，舉個栗子就能比較好的說明了：

假設揹包容量為10，有兩個物品可選，價值分別為：3，2，容量佔用分別為，4，3。

初始狀態：

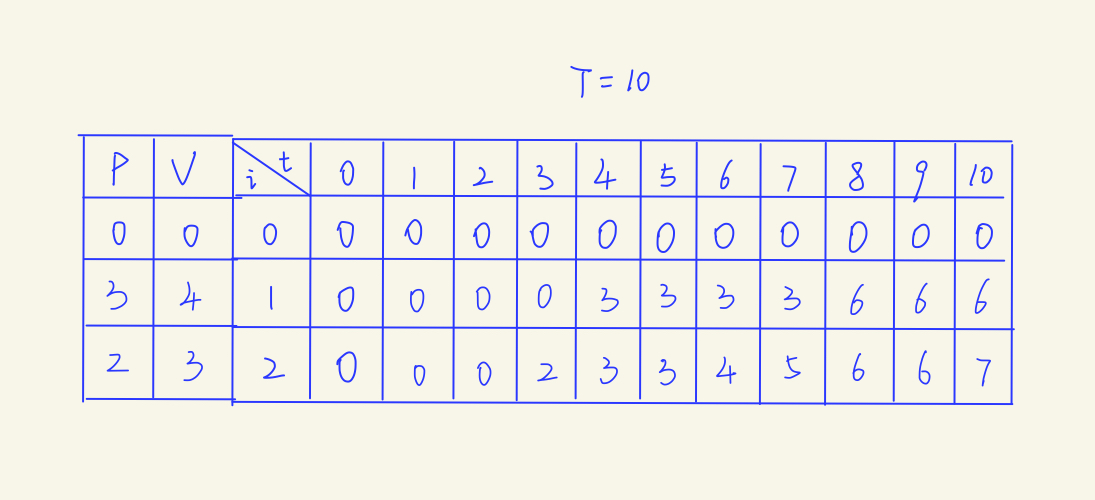
01揹包的填表法：

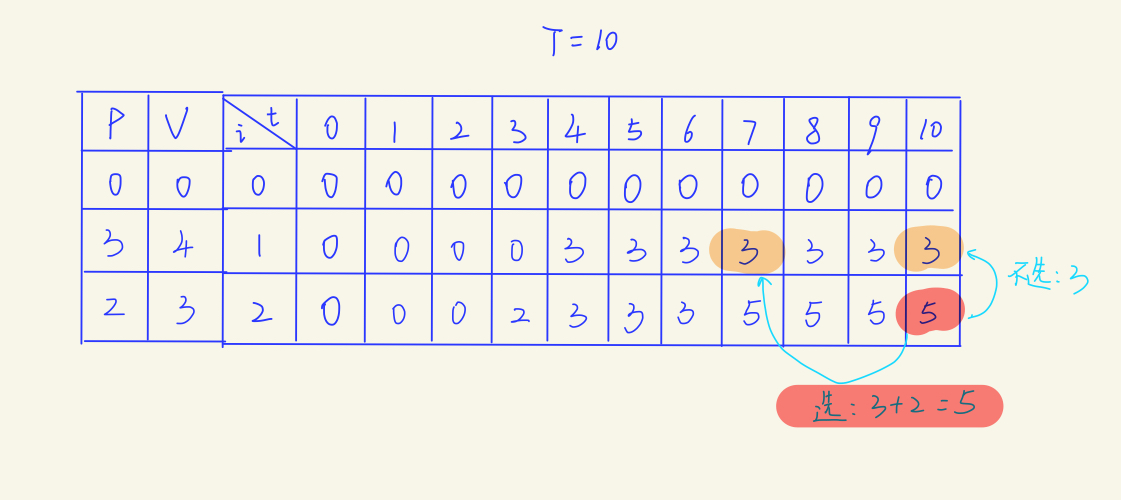
完全揹包的填表法：

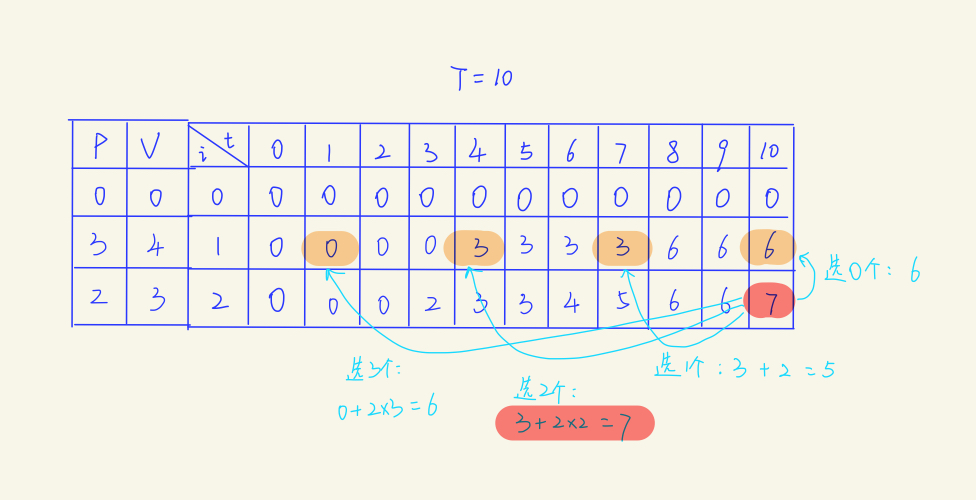
多重揹包的填表法：

假設兩種物品的可選數量分別為：2，1.

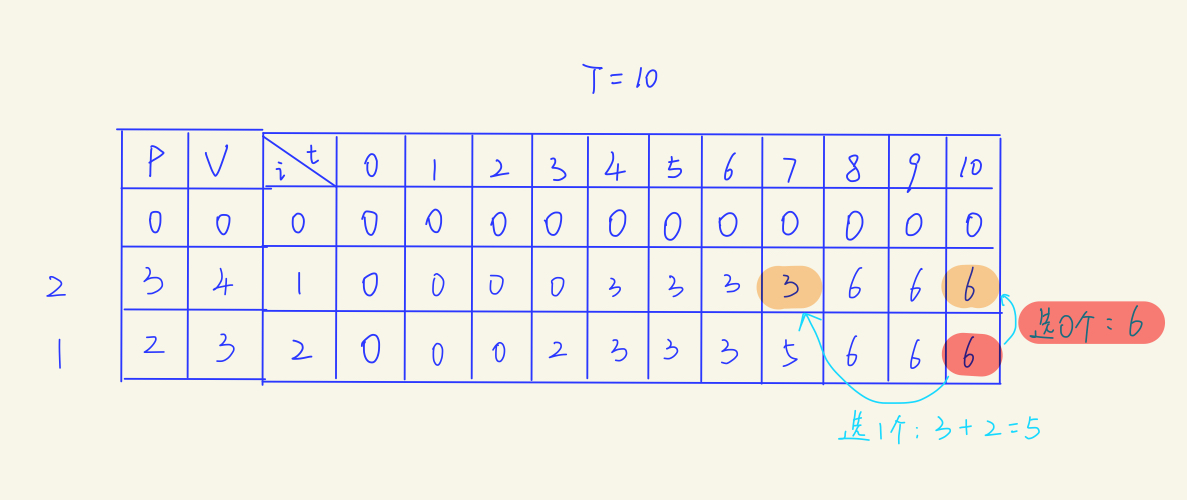
下面再來看看三種揹包問題的一維陣列解決方案。

01揹包：

for i <- 1 to N
    for v <- V to Ci
        F[v] = max{F[v],F[v-Ci] + Wi}

將其核心部分抽象出來：

def ZeroOneKnapsack(F,C,W)
    for v <- V to C
        F[v] = max{F[v],F[v-C] + W}

則01揹包問題可以表示為：

for i <- 1 to N
    ZeroOneKnapsack(F,Ci,Wi)

N代表物品數量，Ci代表第i個物品佔用的容量，V代表揹包總容量，Wi代表第i個物品的價值，下同。

完全揹包：

for i <- 1 to N
    for v <- Ci to V
        F[v] = max{F[v],F[v-Ci] + Wi}

將其核心部分抽象出來：

def CompleteKnapsack(F,C,W)
    for v <- C to V
        F[v] = max{F[v],F[v-C] + W}

則完全揹包問題的解可以表示為：

for i <- 1 to N
    CompleteKnapsack(F,Ci,Wi)

多重揹包：

for i <- 1 to N
    if v < Ci * Mi
        F[v] = max{F[v],F[v-Ci] + Wi}
    else
        for v <- Ci to V
            k <- 1
            while k < M && v > Ci * k
                F[v] = max{F[v],F[v-Ci*k] + Wi*k}
                k++

抽象出核心邏輯：

def MultiKnapsack(F,C,W,M)
    if C * M >= V
        CompleteKnapsack(F,C,W)
        return
    else
        k <- 1
        while k < M
            ZeroOneKnapsack(F,KC,KW)
            k++
        return

則多重揹包問題的解可以表示為：

for i <- 1 to N
    MultiKnapsack(F,Ci,Wi,Mi)

Mi 代表第i件物品最多可選數量

混合揹包問題

現在我們來考慮一種更為複雜的情況，如果可選的物品同時具有上述三種特性，即：有的物品只能選一個，有的物品可以選擇任意多個，有的物品只能選擇有限多個，那麼此時該如何決策呢？

其實有了上面的總結和抽象，這種混合揹包問題就小菜一碟了。

回顧一下上面的三種揹包問題的抽象解，就會發現他們每次都只會考慮一種物品，區別只在於第i個物品的可選策略。所以對於混合揹包問題，同樣也可以一個一個物品考慮，如果這個物品是最多選一個，那麼就採用01揹包的解決策略，如果是可以選擇任意多個，那麼就使用完全揹包的解決策略，如果只能選擇有限多個，那麼就使用多重揹包的解決策略。

虛擬碼如下：

for i <- 1 to N
    if 第i件物品屬於01揹包
        ZeroOneKnapsack(F,Ci,Wi)
    else if 第i件物品屬於完全揹包
        CompleteKnapsack(F,Ci,Wi)
    else if 第i件物品屬於多重揹包
        MultiKnapsack(F,Ci,Wi,Mi)

總結

到此為止，我們就已經比較完美的解決了三種揹包問題，順便還解決了一下混合揹包問題。雖然條件各不相同，但是解題思路卻很相似，相信經過這一篇文章的總結，你對於揹包問題也會有更好的理解，並且領會到這種抽象問題的好處。

當然，更深層次的揹包問題還有很多，比如二維費用問題，物品依賴問題，鑑於博主學疏才淺，暫時也沒有探索的興趣，所以就不一一進行說明了，有興趣的話可以自行搜尋相關內容。

如果本文對你有幫助，不要吝嗇你的點贊哦。也歡迎關注我的公眾號進行留言交流。

文末再贈送一個小福利，關注公眾號並回復： python電子書大全 即可無套路獲得上百本python電子書資源