概述

　　聚類屬於機器學習的無監督學習，在資料中發現數據物件之間的關係，將資料進行分組，組內的相似性越大，組間的差別越大，則聚類效果越好。它跟分類的最主要區別就在於有沒有“標籤”。比如說我們有一組資料，資料對應著每個“標籤”，我們通過這些資料與標籤之間的相關性，預測出某些資料屬於哪些“標籤”，這屬於分類；而聚類是沒有“標籤”的，因此說它屬於無監督學習，分類則屬於監督學習。

　　k-means(k-均值)屬於聚類演算法之一，籠統點說，它的過程是這樣的，先設定引數k，通過歐式距離進行計算，從而將資料集分成k個簇。為了更好地理解這個演算法，下面更加詳細的介紹這個演算法的思想。

演算法思想

　　我們先過一下幾個基本概念：

　（1） K值：即要將資料分為幾個簇；

　（2） 質心：可理解為均值，即向量各個維度取平均值，這個是我們聚類演算法一個重要的指標；

　（3） 歐式距離：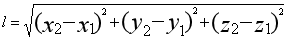

　　上面的這3條基本概念你大可不必太糾結，因為這是為了讓你看下面的內容時，能夠更好理解。假如說，我們現在有一堆資料集，在影象上的分佈是這樣的：

　　從影象上看，貌似可以直接把他分為3個簇，因此，我們設定 k=3，然後我們隨機生成3個點，再通過歐式距離公式，計算每個點到這三個點之間的距離，距離哪個點最近的，就歸類，於是它就變成了這樣：

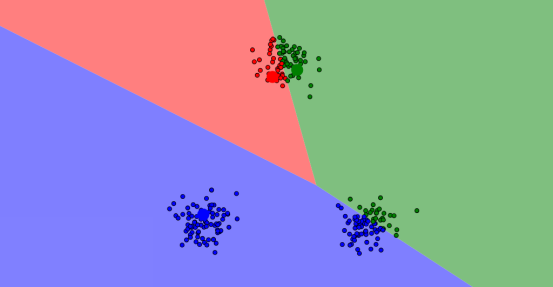
　　當然，這樣還不夠，畢竟這三個點只是隨機生成的，而且我們還需要不斷調整以達到更好的聚類效果；因此我們計算初次分好的簇的均值，即上面提到的質心，讓這三個質心替代掉隨機點，然後迭代重複上面的過程，以達到最優。

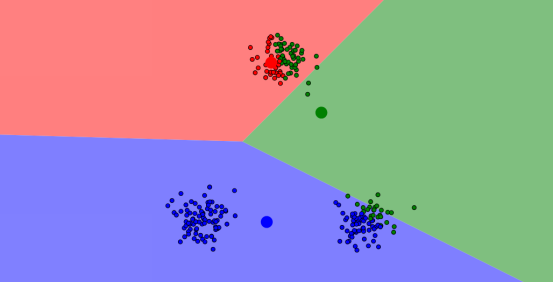
　　......(重複迭代n次)......

　　最後，才生成最優解，如圖：

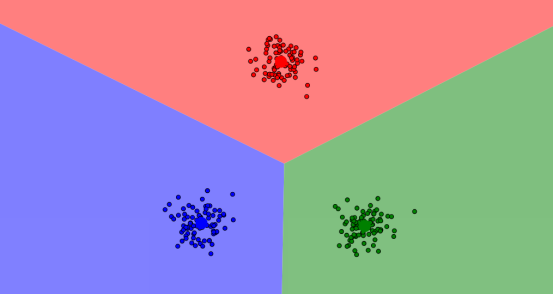
　　上面的圖是在這個網站通過演示得到的，可以上這個網址實際操作一波，加深理解。

 缺點

　　幾乎每個演算法都有其缺點，這個演算法也不例外，優點是原理簡單，實現容易，缺點如下：

　（1）不規則點的聚類結果會有所偏差，如下圖，比如我們想分成4個簇，倆眼睛一嘴巴以及外輪廓，但效果總是難以達到。

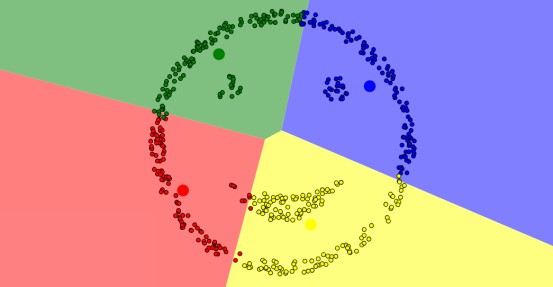
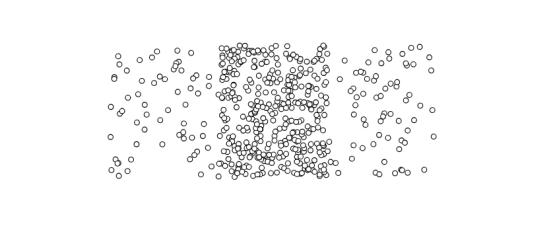
　（2）k值難以確定。比如下面這樣的圖，應該把它從中間分割得到兩塊呢還是分成左中右三塊呢，難以確定。

　　想要第一時間獲取更多有意思的推文，可關注公眾號： Max的日常操作

&n