阿里妹導讀：網際網路黑產盛行，其作弊手段層出不窮，導致廣告效果降低，APP推廣成本暴增。精準識別作弊是網際網路公司和廣告主的殷切期望。今天我們將從時間序列、統計、距離、線性方法、分佈、樹、圖、行為序列、有監督機器學習和深度學習模型等多個角度探討異常檢測。

背景

異常點檢測(Outlier detection)，又稱為離群點檢測，是找出與預期物件的行為差異較大的物件的一個檢測過程。這些被檢測出的物件被稱為異常點或者離群點。異常點檢測在生產生活中有著廣泛應用，比如信用卡反欺詐、工業損毀檢測、廣告點選反作弊等。

異常點（outlier）是一個數據物件，它明顯不同於其他的資料物件。如下圖1所示，N1、N2區域內的點是正常資料。而離N1、N2較遠的O1、O2、O3區域內的點是異常點。

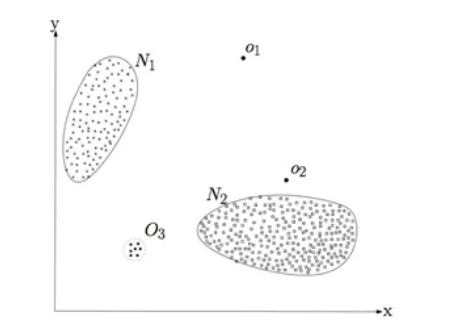
圖1.異常點示例

異常檢測的一大難點是缺少ground truth。常見的方法是先用無監督方法挖掘異常樣本，再用有監督模型融合多個特徵挖掘更多作弊。

近期使用多種演算法挖掘異常點，下面從不同視角介紹異常檢測演算法的原理及其適用場景，考慮到業務特殊性，本文不涉及特徵細節。

1.時間序列

1.1 移動平均（Moving Average，MA）

移動平均是一種分析時間序列的常用工具，它可過濾高頻噪聲和檢測異常點。根據計算方法的不同，常用的移動平均演算法包括簡單移動平均、加權移動平均、指數移動平均。假設移動平均的時間視窗為T，有一個時間序列：

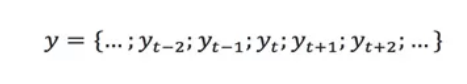
1.1.1 簡單移動平均（Simple Moving Average,SMA）

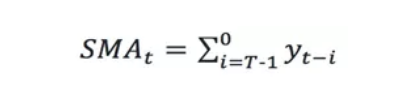
從上面的公式容易看出可以用歷史的值的均值作為當前值的預測值，在序列取值隨時間波動較小的場景中，上述移動均值與該時刻的真實值的差值超過一定閾值則判定該時間的值異常。

適用於：

a.對噪聲資料進行平滑處理，即用移動均值替代當前時刻取值以過濾噪聲；

b.預測未來的取值。

1.1.2 加權移動平均（Weighted Moving Average, WMA）

由於簡單移動平均對視窗內所有的資料點都給予相同的權重，對近期的最新資料不夠敏感，預測值存在滯後性。按著這個思路延伸，自然的想法就是在計算移動平均時，給近期的資料更高的權重，而給視窗內較遠的資料更低的權重，以更快的捕捉近期的變化。由此便得到了加權移動平均和指數移動平均。

加權移動平均比簡單移動平均對近期的變化更加敏感，加權移動平均的滯後性小於簡單移動平均。但由於僅採用線性權重衰減，加權移動平均仍然存在一定的滯後性。

1.1.3 指數移動平均（Exponential Moving Average, EMA）

指數移動平均（Exponential Moving Average, EMA）和加權移動平均類似，但不同之處是各數值的加權按指數遞減，而非線性遞減。此外，在指數衰減中，無論往前看多遠的資料，該期資料的係數都不會衰減到 0，而僅僅是向 0 逼近。因此，指數移動平均實際上是一個無窮級數，即無論多久遠的資料都會在計算當期的指數移動平均數值時，起到一定的作用，只不過離當前太遠的資料的權重非常低。在實際應用中，可以按如下方法得到t時刻的指數移動平均：

其中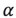表示權重的衰減程度，取值在0和1之間。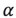越大，過去的觀測值衰減得越快。

1.2 同比和環比

圖2.同比和環比

同比和環比計算公式如圖2所示。適合資料呈週期性規律的場景中。如：1.監控APP的DAU的環比和同比，以及時發現DAU上漲或者下跌；2.監控實時廣告點選、消耗的環比和同比，以及時發現變化。當上述比值超過一定閾值（閾值參考第10部分）則判定出現異常。

1.3 時序指標異常檢測(STL+GESD)

STL是一種單維度時間指標異常檢測演算法。大致思路是：

(1)先將指標做STL時序分解，得到seasonal，trend，residual成分，如圖3所示；
(2)用GESD (generalized extreme studentized deviate)演算法對trend+residual成分進行異常檢測；
(3)為增強對異常點的魯棒性，將GESD演算法中的mean,std等統計量用median, MAD(median absolute deviation)替換；
(4)異常分輸出：abnorm_score = (value - median)/MAD, value為當前值，median為序列的中位數。負分表示異常下跌，正分表示異常上升。

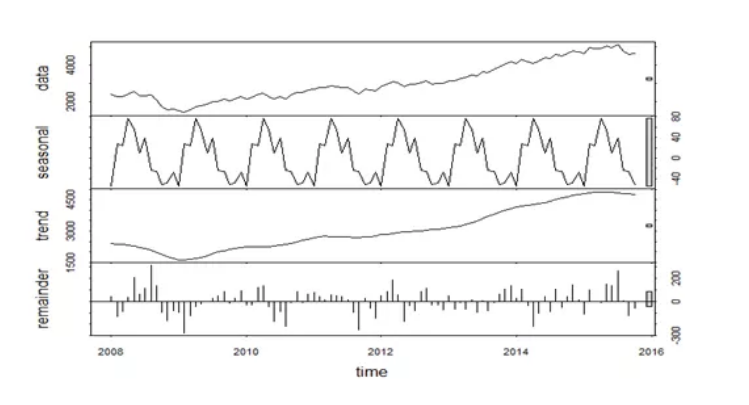
圖3.STL分解示例

2.統計

2.1 單特徵且符合高斯分佈

如果變數x服從高斯分佈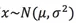：，則其概率密度函式為：

我們可以使用已有的樣本資料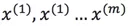來預測總體中的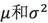，計算方法如下：

2.2 多個不相關特徵且均符合高斯分佈

假設n維的資料集合形如：

且每一個變數均符合高斯分佈，那麼可以計算每個維度的均值和方差

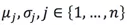，具體來說，對於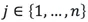，可以計算：

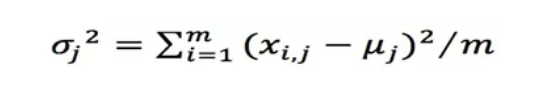
如果有一個新的資料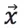，可以計算概率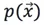如下：

2.3 多個特徵相關，且符合多元高斯分佈

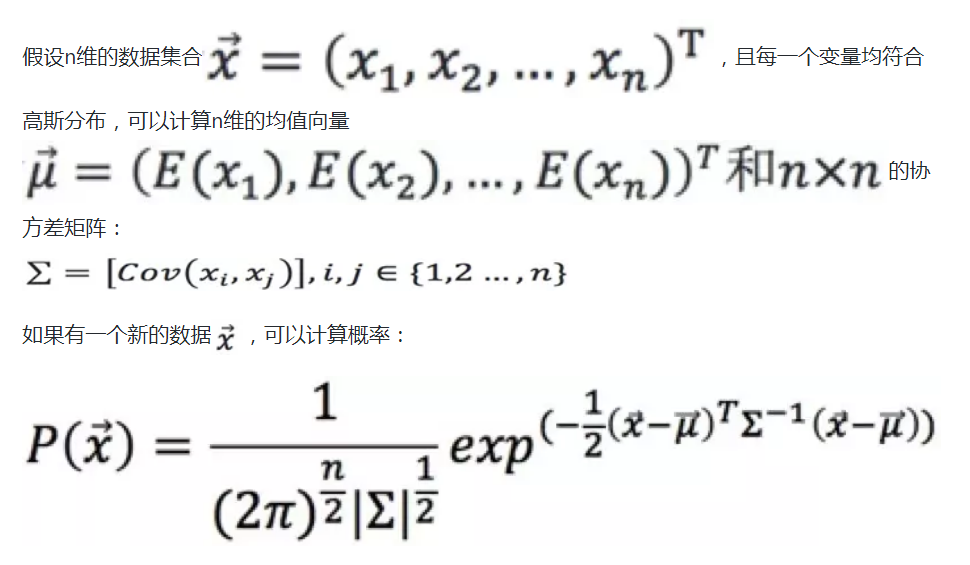
2.4 馬氏距離(Mahalanobis distance)

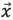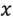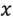對於一個多維列向量的資料集合D，假設是均值向量，那麼對於資料集D中的任意物件，從到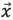的馬氏距離是：

其中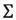是協方差矩陣。可以對數值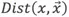進行排序，如果數值過大，那麼就可以認為點是離群點。

2.5 箱線圖

箱線圖演算法不需要資料服從特定分佈，比如資料分佈不符合高斯分佈時可以使用該方法。該方法需要先計算第一四分位數Q1（25%）和第三四分位數Q3（75%）。令IQR=Q3-Q1，然後算出異常值邊界點Q3+λIQR和Q1- λIQR，通常λ取1.5（類似於正態分佈中的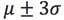，如下圖4所示：

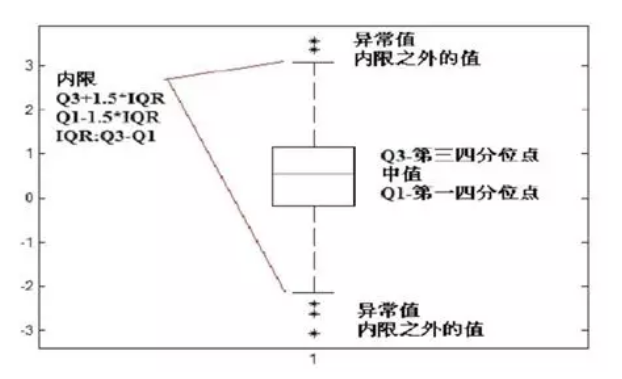
圖4.箱線圖演算法示意圖

3.距離

3.1、基於角度的異常點檢測

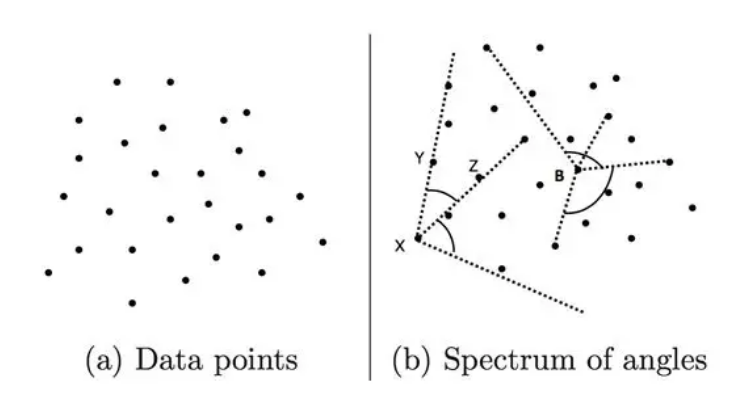
圖5.點集和角度

如上圖5所示，現在有三個點X，Y，Z，和兩個向量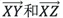，如果對任意不同的點Y，Z，角度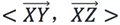變化都較小，則點X是異常點。通過餘弦夾角公式易得角度：

D是點集，則對於任意不同的點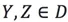，點X的所有角度的方差為：

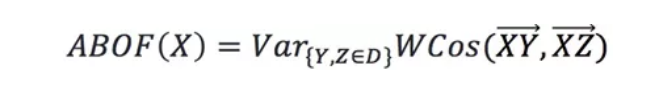
異常點的上述方差較小。該演算法的時間複雜度是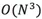，適合資料量N較小的場景。

3.2 基於KNN的異常點檢測

D是點集，則對於任意點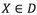，計算其K近鄰的距離之和Dist(K,X)。Dist(K,X)越大的點越異常。時間複雜度是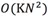，其中N是資料量的大小。

4.線性方法（矩陣分解和PCA降維）

基於矩陣分解的異常點檢測方法的主要思想是利用主成分分析（PCA）去尋找那些違反了資料之間相關性的異常點。為了找到這些異常點，基於主成分分析的演算法會把資料從原始空間投影到主成分空間，然後再從主成分空間投影回原始空間。對於大多數的資料而言，如果只使用第一主成分來進行投影和重構，重構之後的誤差是較小的；但是對於異常點而言，重構之後的誤差相對較大。這是因為第一主成分反映了正常點的方差，最後一個主成分反映了異常點的方差。

假設X是一個p維的資料集合，有N個樣本，它的協方差矩陣是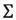。那麼協方差矩陣就可以分解為：

其中P是一個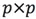維正交矩陣，它的每一列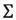都是的特徵向量。D是一個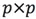維對角矩陣，包含了特徵值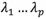。在圖形上，一個特徵向量可以看成2維平面上的一條線，或者高維空間裡面的一個平面。特徵向量所對應的特徵值反映了這批資料在這個方向上的拉伸程度。通常情況下，將特徵值矩陣D中的特徵值從大到小的排序，特徵向量矩陣P的每一列也進行相應的調整。

資料集X在主成分空間的投影可以寫成Y=XP，注意可以只在部分的維度上做投影，使用top-j的主成分投影之後的矩陣為：。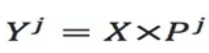

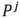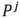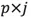其中是矩陣P的前j列，也就是說是一個維的矩陣。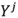是矩陣Y的前j列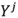，是一個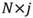維的矩陣。按同樣的方式從主成分空間對映到原始空間，重構之後的資料集合是 。

其中是使用top-j的主成分重構之後的資料集，是一個維的矩陣。如圖6所示：

圖6.矩陣變換示意圖

定義資料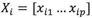
的異常值分為：

其中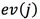表示的是top-j主成分佔所有主成分的比例，特徵值是按照從大到小的順序排列的。因此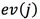是遞增的，這就意味著j越大，越多的方差就會被算到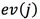中，因為是從 1 到 j 的求和。在這個定義下，偏差最大的第一個主成分獲得最小的權重，偏差最小的最後一個主成分獲得了最大的權重1。根據 PCA 的性質，異常點在最後一個主成分上有著較大的偏差，因此會有更大的異常分。

5.分佈

即對比基準流量和待檢測流量的某個特徵的分佈。

5.1 相對熵（KL散度）

相對熵（KL散度）可以衡量兩個隨機分佈之間的距離，當兩個隨機分佈相同時，它們的相對熵為零，當兩個隨機分佈的差別增大時，它們的相對熵也會增大。所以相對熵可以用於比較兩個分佈的相似度。設是兩個概率分佈的取值，則對應相對熵為。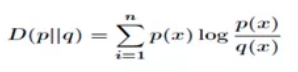

5.2 卡方檢驗

卡方檢驗通過檢驗統計量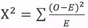來比較期望結果和實際結果之間的差別，然後得出實際結果發生的概率。其中O代表觀察值，E代表期望值。這個檢驗統計量提供了一種期望值與觀察值之間差異的度量辦法。最後根據設定的顯著性水平查詢卡方概率表來判定。

6.樹（孤立森林）

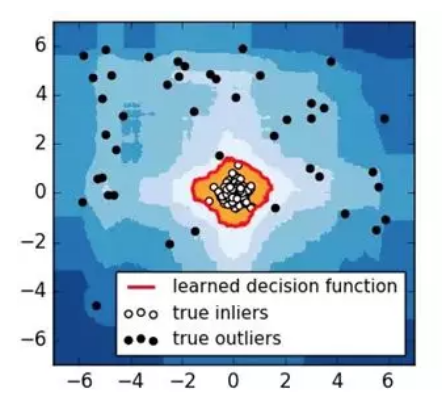
圖7.iForest檢測結果

孤立森林（Isolation Forest）假設我們用一個隨機超平面來切割資料空間, 每切一次便可以生成兩個子空間。接著繼續用一個隨機超平面來切割每個子空間，迴圈下去，直到每個子空間裡面只有一個數據點為止。那些密度很高的簇是需要被切很多次才能讓子空間中只有一個數據點，但是那些密度很低的點的子空間則很快就被切割成只有一個數據點。如圖7所示，黑色的點是異常點，被切幾次就停到一個子空間；白色點為正常點，白色點聚焦在一個簇中。孤立森林檢測到的異常邊界為圖7中紅色線條，它能正確地檢測到所有黑色異常點。

如圖8所示，用iForest切割4個數據，b和c的高度為3，a的高度為2，d的高度為1，d最先被孤立，它最有可能異常。

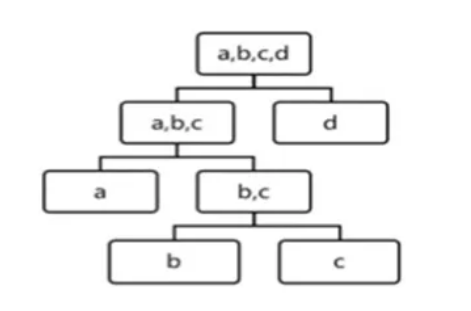
圖8.iForest切割過程

7.圖

7.1 最大聯通圖

在無向圖G中，若從頂點A到頂點B有路徑相連，則稱A和B是連通的；在圖G中存在若干子圖，其中每個子圖中所有頂點之間都是連通的，但不同子圖間不存在頂點連通，那麼稱圖G的這些子圖為最大連通子圖。

如圖9所示，device是裝置id，mbr是會員id，節點之間有邊表示裝置上有對應的會員登入過，容易看出device_1、device_2、device_3、device_4是同人，可以根據場景用於判斷作弊，常用於挖掘團伙作弊。

圖9.最大聯通圖結果

最大聯通圖的前提條件是每條邊必須置信。適用場景：找所有連通關係。當資料中存在不太置信的邊時，需要先剔除髒資料，否則會影響最大聯通圖的效果。

7.2 標籤傳播聚類

標籤傳播圖聚類演算法是根據圖的拓撲結構，進行子圖的劃分，使得子圖內部節點的連線較多，子圖之間的連線較少。標籤傳播演算法的基本思路是節點的標籤依賴其鄰居節點的標籤資訊，影響程度由節點相似度決定，通過傳播迭代更新達到穩定。圖10中的節點經標籤傳播聚類後將得2個子圖，其中節點1、2、3、4屬於一個子圖，節點5、6、7、8屬於一個子圖。

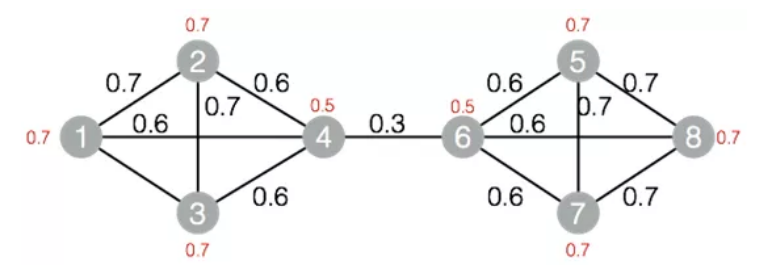
圖10.標籤傳播聚類演算法的圖結構

標籤傳播聚類的子圖間可以有少量連線。適用場景：節點之間“高內聚低耦合”。圖10用最大聯通圖得1個子圖，用標籤傳播聚類得2個子圖。

8.行為序列（馬爾科夫鏈）

如圖11所示，使用者在搜尋引擎上有5個行為狀態：頁面請求（P），搜尋（S），自然搜尋結果（W），廣告點選（O），翻頁（N）。狀態之間有轉移概率，由若干行為狀態組成的一條鏈可以看做一條馬爾科夫鏈。

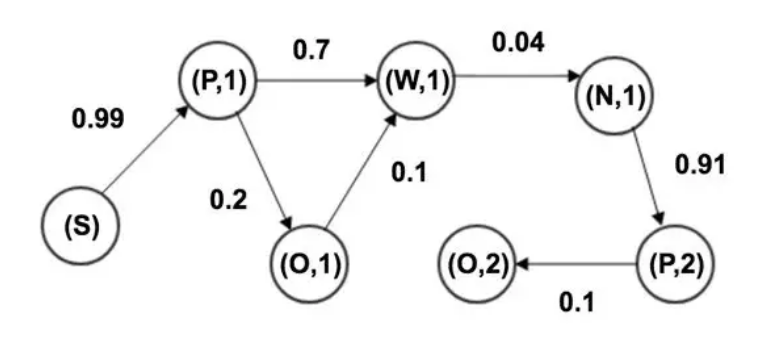
圖11.使用者行為狀態圖

統計正常行為序列中任意兩個相鄰的狀態，然後計算每個狀態轉移到其他任意狀態的概率，得狀態轉移矩陣。針對每一個待檢測使用者行為序列，易得該序列的概率值，概率值越大，越像正常使用者行為。

9.有監督模型

上述方法都是無監督方法，實現和理解相對簡單。但是由於部分方法每次使用較少的特徵，為了全方位攔截作弊，需要維護較多策略；另外上述部分方法組合多特徵的效果取決於人工經驗。而有監督模型能自動組合較多特徵，具備更強的泛化能力。

9.1 機器學習模型GBDT

樣本：使用前面的無監督方法挖掘的作弊樣本作為訓練樣本。如果作弊樣本仍然較少，用SMOTE或者GAN生成作弊樣本。然後訓練GBDT模型，用轉化資料評估模型的效果。

9.2 深度學習模型Wide&Deep

Wide&Deep通過分別提取wide特徵和deep特徵，再將其融合在一起訓練，模型結構如圖12所示。wide是指高維特徵和特徵組合的LR。LR高效、容易規模化（scalable）、可解釋性強。出現的特徵組合如果被不斷加強，對模型的判斷起到記憶作用。但是相反的泛化性弱。

deep則是利用神經網路自由組合對映特徵，泛化性強。deep部分本質上挖掘一些樣本特徵的更通用的特點然後用於判斷，但是有過度泛化的風險。

演算法通過兩種特徵的組合去平衡記憶（memorization）和泛化（ generalization）。

為了進一步增加模型的泛化能力，可以使用前面的無監督方法挖掘的作弊樣本作為訓練樣本，訓練Wide&Deep模型識別作弊。

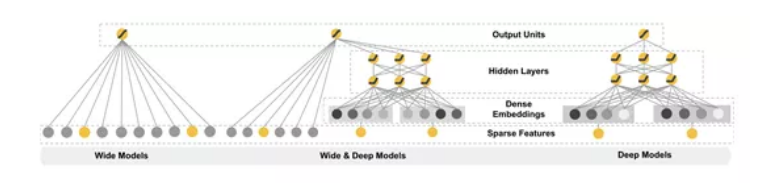
圖12.Wide&Deep模型

10.其他問題

10.1 常用選擇閾值的思路

上述各種方法都需要計算異常閾值，可以用下述思路先選閾值，再用轉化資料驗證該閾值的合理性。

a.無監督方法：使用分位點定閾值、找歷史資料的分佈曲線的拐點；

b.有監督模型：看驗證集的準召曲線

10.2 非高斯分佈轉高斯分佈

有些特徵不符合高斯分佈，那麼可以通過一些函式變換使其符合高斯分佈，以便於使用上述統計方法。常用的變換函式：，其中c為非負常數；，c為0-1之間的一個分數。

原文連結
本文為雲棲社群原創內容，未經