為什麼選擇B+樹作為資料庫索引結構?
背景
首先,來談談B樹。為什麼要使用B樹?我們需要明白以下兩個事實:
【事實1】
不同容量的儲存器,訪問速度差異懸殊。以磁碟和記憶體為例,訪問磁碟的時間大概是ms級的,訪問記憶體的時間大概是ns級的。有個形象的比喻,若一次記憶體訪問需要1秒,則一次外存訪問需要1天。所以,現在的儲存系統,都是分級組織的。最常用的資料儘可能放在更高層、更小的儲存器中,只有在當前層找不到,才向更低層、更大的儲存器中尋找。這也就解釋了,當處理大規模資料的時候(指無法將資料一次性存入記憶體),演算法的實際執行時間,往往取決於資料在不同儲存級別之間的IO次數。因此,要想提升速度,關鍵在於減少IO。
【事實2】
磁碟讀取資料是以資料塊(block)(或者:頁,page)為基本單位的,位於同一資料塊中的所有資料都能被一次性全部讀取出來。換句話說,從磁碟中讀1B,與讀1KB幾乎一樣快!因此,想要提升速度,應該利用外存批量訪問的特點,在一些文章中,也稱其為磁碟預讀。系統之所以這麼設計,是基於一個著名的區域性性原理:
當一個數據被用到時,其附近的資料也通常會馬上被使用,程式執行期間所需要的資料通常比較集中
B樹
假設有10億條記錄(1000*1000*1000),如果使用平衡二叉搜尋樹(Balanced Binary Search Tree, BBST),最壞的情況下,查詢需要log(2, 10^9) = 30次 I/O 操作,且每次只能讀出一個關鍵字(即如果這次讀出來的關鍵字不是我要查詢的,就要再進行一次I/O去讀取資料)。如果換成B樹,會是怎樣的情況呢?
B 樹是為了磁碟或其它輔助儲存裝置而設計的一種多叉平衡搜尋樹。多級儲存系統中使用B樹,可針對外部查詢,大大減少I/O次數。通過B樹,可充分利用外存對批量訪問的高效支援,將此特點轉化為優點。每下降一層,都以超級結點為單位(超級結點就是指一個結點內包含多個關鍵字),從磁碟中讀入一組關鍵字。那麼,具體多大為一組呢?
一個節點存放多少資料視磁碟的資料塊大小而定,比如磁碟中1 block的大小有1024KB,假設每個關鍵字的大小為 4 Byte,則可設定每一組的大小m = 1024 KB / 4 Byte = 256。目前,多數資料庫系統採用 m = 200~300。假設取m = 256,則B樹儲存1億條資料的樹的高度大概是 log(256, 10^9) = 4,也就是單次查詢所需要進行的I/O次數不超過 4 次,由此大大減少了I/O次數。
一般來說,B樹的根節點常駐於記憶體中,B樹的查詢過程是這樣的:首先,由於一個節點內包含多個(比如,是256個)關鍵碼,所以需要先順序/二分來查詢,如果找到則查詢成功;如果失敗,則根據相應的引用從磁碟中讀入下一層的節點資料(這裡就涉及到一次磁碟I/O),同樣的在節點內順序查詢,如此往復進行...事實上,B樹查詢所消耗的時間很大一部分花在了I/O上,所以減少I/O次數是非常重要的。
B樹的定義
B樹就是平衡的多路搜尋樹,所謂的m階B樹,即m路平衡搜尋樹。根據維基百科的定義,一棵m階B樹需滿足以下要求:
- 每個結點至多含有m個分支節點(m>=2)。
- 除根結點之外的每個非葉結點,至少含有┌m/2┐個分支。
- 若根結點不是葉子結點,則至少有2個孩子。
- 一個含有k個孩子的非葉結點包含k-1個關鍵字。 (每個結點內的關鍵字按升序排列)
- 所有的葉子結點都出現在同一層。實際上這些結點並不存在,可以看作是外部結點。
根據節點的分支的上下限,也可以稱其為(┌m/2┐, m)樹。比如,階數m=4時,這樣的B樹也可以稱為(2,4)樹。(事實上,(2,4)樹是一棵比較特殊的B樹,它和紅黑樹有著特別的淵源!後面談及紅黑樹時會談到。)
並且,每個內部結點的關鍵字都作為其子樹的分隔值。比如,某結點含有2個關鍵字(假設為a1和a2),也就是說該結點含有3個子樹。那麼,最左子樹的關鍵字均小於a1;中間子樹的關鍵字介於a1~a2;最右子樹的關鍵字均大於a2。
示例,一棵3階的B樹是這個樣子:
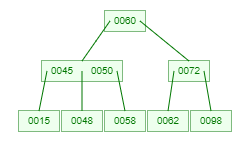
B樹的高度(瞭解)
假定一棵B樹非空,具有n個關鍵字、高度為h(令根結點為第1層)、階數為m,那麼該B樹的最大高度和最小高度分別是多少?
最大高度
當樹的高度最大時,則每個結點含有的關鍵字數應該儘量少。根據定義,根結點至少有2個孩子(即1個關鍵字),除根結點之外的非葉結點至少有┌m/2┐個孩子(即┌m/2┐-1個關鍵字),為了描述方便,這裡令p = ┌m/2┐。
第1層 1個結點 (含1個關鍵字)
第2層 2個結點 (含2*(p-1)個關鍵字)
第3層 2p個結點 (含2p*(p-1)^2個關鍵字)
...
第h層 2p^(h-2)個結點
故總的結點個數n
≥ 1+(p-1)*[2+2p+2p^2+...+2p^(h-2)]
≥ 2p^(h-1)-1
從而推匯出 h ≤ log_p[(n+1)/2] + 1 (其中p為底數,p=┌m/2┐)最小高度
當樹的高度最低時,則每個結點的關鍵字都至多含有m個孩子(即m-1個關鍵字),則有
n ≤ (m-1)*(1 + m + m^2 +...+ m^(h-1)) = m^h - 1
從而推匯出 h ≥ log_m(n+1) (其中m為底數)B+樹
B+樹的定義
B+樹是B樹的一個變體,B+樹與B樹最大的區別在於:
- 葉子結點包含全部關鍵字以及指向相應記錄的指標,而且葉結點中的關鍵字按大小順序排列,相鄰葉結點用指標連線。
- 非葉結點僅儲存其子樹的最大(或最小)關鍵字,可以看成是索引。
一棵3階的B+樹示例:(好好體會和B樹的區別,兩者的關鍵字是一樣的)
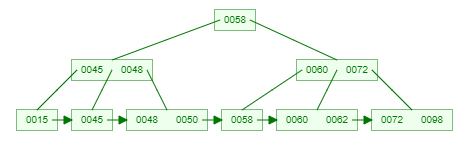
問:為什麼說B+樹比B樹更適合實際應用中作業系統的檔案索引和資料庫索引?
答:
- B+樹更適合外部儲存。由於內結點不存放真正的資料(只是存放其子樹的最大或最小的關鍵字,作為索引),一個結點可以儲存更多的關鍵字,每個結點能索引的範圍更大更精確,也意味著B+樹單次磁碟IO的資訊量大於B樹,I/O的次數相對減少。
- MySQL是一種關係型資料庫,區間訪問是常見的一種情況,B+樹葉結點增加的鏈指標,加強了區間訪問性,可使用在區間查詢的場景;而使用B樹則無法進行區間查詢。
參考:
1)清華大學鄧俊輝資料結構-高階搜尋樹
2)https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html (資料結構視覺化
