NN入門,手把手教你用Numpy手撕NN(一)
前言
這是一篇包含極少數學推導的NN入門文章
大概從今年4月份起就想著學一學NN,但是無奈平時時間不多,而且空閒時間都拿去做比賽或是看動漫去了,所以一拖再拖,直到這8月份才正式開始NN的學習。
這篇文章主要參考了《深度學習入門:基於Python的理論與實現》一書,感覺這本書很不錯,偏向實踐,蠻適合入門。
話不多說,下面開始我們的NN入門(手撕NN)之旅
基礎數學知識
這裡只對張量進行簡單介紹,關於矩陣運算之類的,就靠你們自己另外學啦。
標量(0D張量)
僅包含一個數字的張量叫作標量(scalar,也叫標量張量、零維張量、0D 張量)。在 Numpy 中,一個 float32 或 float64 的數字就是一個標量張量(或標量陣列)。你可以用 ndim 屬性來檢視一個 Numpy 張量的軸的個數。
>>> import numpy as np
>>> x = np.array(1)
>>> x
array(1)
>>> x.ndim
0向量(1D張量)
數字組成的陣列叫作向量(vector)或一維張量(1D 張量)。一維張量只有一個軸。下面是 一個 Numpy 向量。
>>> x = np.array([1, 2, 3, 4, 5])
>>> x
array([1, 2, 3, 4, 5])
>>> x.ndim
1 這個向量有5 個元素,也被稱為5D 向量。
矩陣(2D張量)
向量組成的陣列叫作矩陣(matrix)或二維張量(2D 張量)。矩陣有 2 個軸(通常叫作行和列),下面是一個 Numpy 矩陣。
>>> x = np.array([[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]])
>>> x.ndim
2 第一個軸上的元素叫作行(row),第二個軸上的元素叫作列(column)。在上面的例子中, [5, 78, 2, 34, 0] 是 x 的第一行,[5, 6, 7] 是第一列。
3D張量與更高維張量
將多個矩陣組合成一個新的陣列,可以得到一個3D 張量,可以將其直觀地理解為數字 組成的立方體。下面是一個 Numpy 的 3D 張量。
>>> x = np.array([[[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]],
[[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]],
[[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]]])
>>> x.ndim
3 將多個3D 張量組合成一個數組,可以建立一個4D 張量,以此類推。深度學習處理的一般 是 0D 到 4D 的張量,但處理視訊資料時可能會遇到 5D 張量。
神經網路(Neural Network)
神經網路實際上是由多個層(神經網路的基本資料結構)堆疊而成,層是一個數據處理模組,可以將一個 或多個輸入張量轉換為一個或多個輸出張量。下圖是一個最簡單的網路

這是一個三層神經網路(但實質上只有2層神經元有權重,因此也可稱其為“2層網路”),包括輸入層、中間層(隱藏層)和輸出層。(個人認為,對於任意一個網路,都可以簡化成上圖所示的一個三層的神經網路,資料從輸入層進入,經過一層運算進入隱藏層,然後在隱藏層中進行各種運算,最後再通過一層運算到達輸出層,輸出我們所需的結果)。
那麼,對於一個最簡單的網路,每一層的運算是如何的呢?
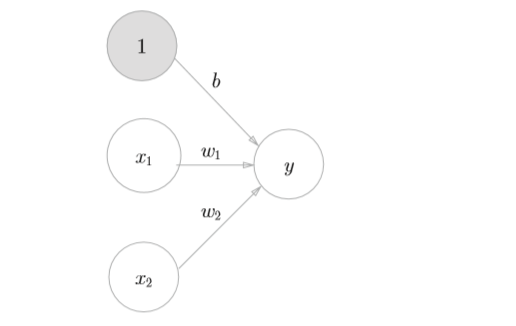
如上圖所示,假設我們輸入了 \(x_1, x_2\), \(x_1, x_2\) 分別乘上到下一層的權重,再加上偏置,得到一個y值,這個y值將作為下一層的輸入,用公式表達如下
\[
y = w_1x_1+w_2x_2+b {\tag 1}
\]
可想而知,如果所有的計算都是這樣的話,那神經網路就只是一個線性模型,那要如何使其具有非線性呢?
很簡單,可以加入啟用函式\(h(x)\),那麼,我們的公式便可改成
\[
a=w_1x_1+w_2x_2+b {\tag {2.1}}
\]
\[ y=h(a) {\tag {2.2}} \]
首先,式(2.1)計算加權輸入訊號和偏置的總和,記為a。然後,式(2.2) 用h(x)函式將a轉換為輸出y。
啟用函式
這裡介紹下常用的啟用函式
sigmoid函式
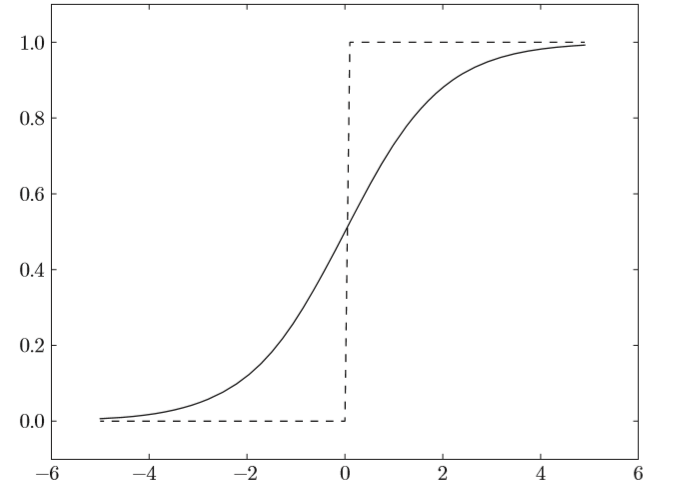
說到非線性,比較容易想到的應該是階躍函式,比如下面程式碼所示的
def step_function(x):
if x > 0:
return 1
else:
return 0但是,由於階躍函式只有兩個值,不存在平滑性,在計算過程中表示能力肯定不夠好,所以,又想到sigmoid函式
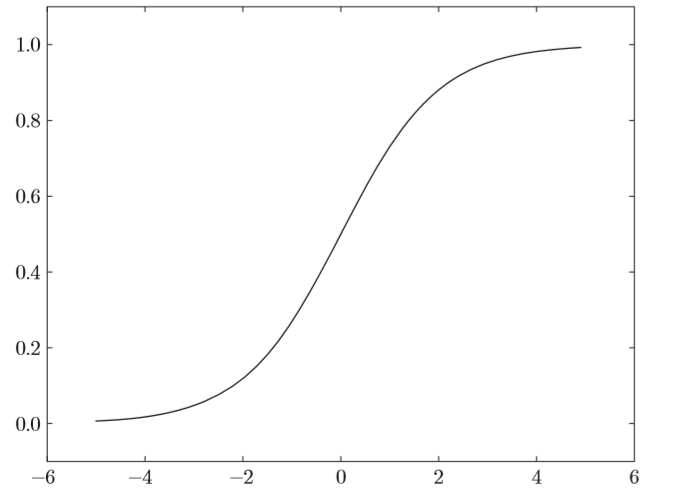
def sigmoid(x):
return 1 / (1 + np.exp(-x))sigmoid函式的平滑性對神經網路的學習具有重要意義。
ReLU函式
在神經網路發展的歷史上,sigmoid函式很早就開始被使用了,而最近則主要使用ReLU(Rectified Linear Unit)函式。
\[
h(x)=
\begin{cases}
x,\quad x > 0\\
0,\quad x<=0
\end{cases}
\tag{3}
\]
def relu(x):
return np.maximum(0, x)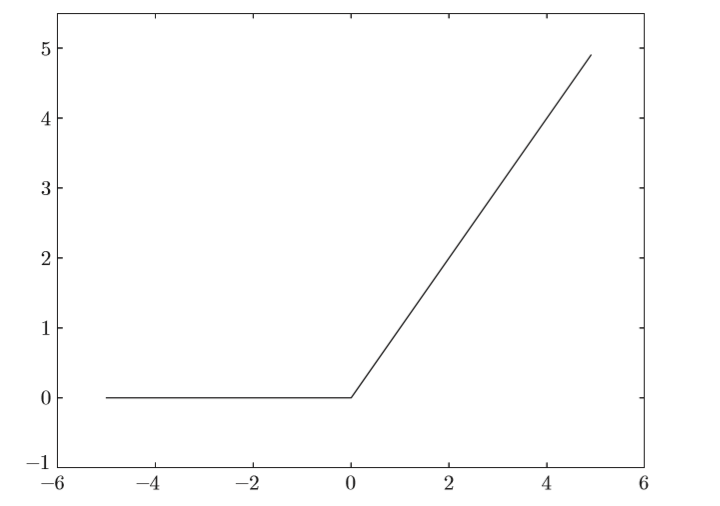
恆等函式和softmax函式(輸出層啟用函式)
神經網路可以用在分類問題和迴歸問題上,不過需要根據情況改變輸出 層的啟用函式。一般而言,迴歸問題用恆等函式,分類問題用softmax函式。
恆等函式會將輸入按原樣輸出,對於輸入的資訊,不加以任何改動地直 接輸出。因此,在輸出層使用恆等函式時,輸入訊號會原封不動地被輸出。
分類問題中使用的softmax函式可以用下面的式子表示。
\[
y_k = \frac{exp(a_k)}{\sum^n_{i=1}exp(a_i)} \tag{4}
\]
def softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y上面的softmax函式的實現在計算機的運算上存在有溢位問題。softmax函式的實現中要進行指數函式的運算,但是此時指數函式的值很容易變得非常大。比如,\(e^{10}\)的值 會超過20000,\(e^{100}\)會變成一個後面有40多個0的超大值,\(e^{1000}\)的結果會返回 一個表示無窮大的inf。如果在這些超大值之間進行除法運算,結果會出現“不確定”的情況。
因此對softmax做如下改進
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c) # 溢位對策
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
網路的學習
從之前的介紹來看,設定好神經網路的引數,設定好啟用函式,似乎就可以利用該神經網路來做預測了,事實也是入此。但這裡存在一個很重要的問題,網路的各個權重引數如何設定?1. 人為設定,這好像就成了人工神經網路,並且十分不現實,一旦網路結構比較大,具有數萬個神經元的時候,完全無法設定引數。2. 從資料中學習,這是所有機器學習、深度學習模型的一個很重要的特徵,從資料中學習。
下面將介紹神經網路在學習中需要的一些東西
損失函式(loss function)
相信有機器學習基礎的對此都不陌生。神經網路每次在學習時,會更新一組權重,通過這組新的權重然後產生一組預測值,那我們如何判斷這組權重是否是較優的呢?通過損失函式即可,這裡介紹兩個損失函式(可跳過)。
損失函式是表示神經網路效能的“惡劣程度”的指標,即當前的 神經網路對監督資料在多大程度上不擬合,在多大程度上不一致。 以“效能的惡劣程度”為指標可能會使人感到不太自然,但是如 果給損失函式乘上一個負值,就可以解釋為“在多大程度上不壞”, 即“效能有多好”。並且,“使效能的惡劣程度達到最小”和“使性 能的優良程度達到最大”是等價的,不管是用“惡劣程度”還是“優 良程度”,做的事情本質上都是一樣的。
均方誤差(mean squared error)
\[ E=\frac{1}{2}\sum_k(y_k-t_k)^2 \tag{5} \]
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)
該損失函式常用於迴歸問題
交叉熵誤差(cross entropy error)
\[ E=-\sum_k{t_klogy_k} \tag{6} \]
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))
這裡,引數y和t是NumPy陣列。函式內部在計算np.log時,加上了一 個微小值delta。這是因為,當出現np.log(0)時,np.log(0)會變為負無限大的-inf,這樣一來就會導致後續計算無法進行。作為保護性對策,新增一個微小值可以防止負無限大的發生。
交叉熵誤差常用於分類問題上
mini-batch 學習
介紹了損失函式之後,其實已經可以利用損失函式開始訓練我們的神經網路了,但是,我們每次訓練都不止一條資料,如果想要訓練出比較好的神經網路模型,在計算損失函式時就必須將所有的訓練資料作為物件。以交叉熵誤差為例,損失函式改寫成下面的式子
\[
E=-\frac{1}{N}\sum_n\sum_kt_{nk}logy_{nk} \tag{7}
\]
但是,同時需考慮,在MNIST資料集中,訓練資料有60000條,如果以全部資料為物件求損失函式的和,則計算過程需要花費較長的時間。再者,如果遇到大資料, 資料量會有幾百萬、幾千萬之多,這種情況下以全部資料為物件計算損失函式是不現實的。因此,我們從全部資料中選出一部分,作為全部資料的“近似”。神經網路的學習也是從訓練資料中選出一批資料(稱為mini-batch,小 批量),然後對每個mini-batch進行學習。比如,從60000個訓練資料中隨機選擇200筆,再用這200筆資料進行學習。這種學習方式稱為mini-batch學習。
此時交叉熵程式碼實現如下
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7)) / batch_size
當監督資料是標籤形式(非one-hot表示,而是像“2”“ 7”這樣的標籤)時,交叉熵誤差可通過如下程式碼實現。
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
引數(權重和偏置)優化
上面介紹了更新權重時需要的損失函式,但是,我們要如何利用損失函式來更新權重呢?這裡用到了我們熟知的梯度法。
梯度法
機器學習的主要任務是在學習時尋找最優引數。同樣地,神經網路也必 須在學習時找到最優引數(權重和偏置)。這裡所說的最優引數是指損失函式取最小值時的引數。但是,一般而言,損失函式很複雜,引數空間龐大,我 們不知道它在何處能取得最小值。而通過巧妙地使用梯度來尋找函式最小值 (或者儘可能小的值)的方法就是梯度法,數學表示如下
\[
x_0=x_0-\eta \frac{\partial f}{\partial x_0} \\
x_1=x_1-\eta \frac{\partial f}{\partial x_1} \tag{8}
\]
式中η表示更新量,在神經網路的學習中,稱為學習率(learning rate)。學習率決定在一次學習中,應該學習多少,以及在多大程度上更新引數。
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x) # 生成和x形狀相同的陣列
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
# f(x+h)的計算
x[idx] = tmp_val + h
fxh1 = f(x)
# f(x-h)的計算
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 還原值
it.iternext()
return grad
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
for i in range(step_num):
grad = numerical_gradient(f, x)
x -= lr * grad
return x
引數f是要進行最優化的函式,init_x是初始值,lr是學習率learning rate,step_num是梯度法的重複次數。numerical_gradient(f,x)會求函式的梯度,用該梯度乘以學習率得到的值進行更新操作,由step_num指定重複的 次數。
學習率需要事先確定為某個值,比如0.01或0.001。一般而言,這個值 過大或過小,都無法抵達一個“好的位置”。在神經網路的學習中,一般會 一邊改變學習率的值,一邊確認學習是否正確進行了。
神經網路的梯度
\[ \mathbf{W}=\left( \begin{matrix} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \end{matrix} \right) \\ \frac{\partial L}{\partial \mathbf{W}} = \left( \begin{matrix} \frac{\partial L}{\partial w_{11}} & \frac{\partial L}{\partial w_{12}} &\frac{\partial L}{\partial w_{13}} \\ \frac{\partial L}{\partial w_{21}} & \frac{\partial L}{\partial w_{22}} &\frac{\partial L}{\partial w_{23}} \end{matrix} \right) \tag{9} \]
就是需要一個一個算比較麻煩,但是計算機就無所謂了
迭代虛擬碼如下
def f(W):
return net.loss(x, t)
dW = numerical_gradient(f, net.W)
學習演算法的實現
根據前面的介紹,差不多可以理清神經網路的學習步驟了
mini-batch
從訓練資料中隨機選出一部分資料,這部分資料稱為mini-batch。我們 的目標是減小mini-batch的損失函式的值。
梯度計算
為了減小mini-batch的損失函式的值,需要求出各個權重引數的梯度。 梯度表示損失函式的值減小最多的方向。
更新引數
將權重引數沿梯度方向進行微小更新。
迭代
重複步驟1、步驟2、步驟3。
神經網路的學習按照上面4個步驟進行。這個方法通過梯度下降法更新引數,不過因為這裡使用的資料是隨機選擇的mini batch資料,所以又稱為 隨機梯度下降法(stochastic gradient descent)。
下面給出一個兩層的簡單神經網路的實現
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
"""
:param: input_size - 輸入層的神經元數
:param: hidden_size - 隱藏層的神經元數
;param: output_size - 輸出層的神經元數
"""
# 初始化權重
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size) self.params['b2'] = np.zeros(output_size)
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
# x:輸入資料, t:監督資料
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# x:輸入資料, t:監督資料
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
訓練
# 資料載入程式碼
try:
import urllib.request
except ImportError:
raise ImportError('You should use Python 3.x')
import os.path
import gzip
import pickle
import os
import numpy as np
url_base = 'http://yann.lecun.com/exdb/mnist/'
key_file = {
'train_img':'train-images-idx3-ubyte.gz',
'train_label':'train-labels-idx1-ubyte.gz',
'test_img':'t10k-images-idx3-ubyte.gz',
'test_label':'t10k-labels-idx1-ubyte.gz'
}
dataset_dir = os.path.dirname(os.path.abspath(__file__))
save_file = dataset_dir + "/mnist.pkl"
train_num = 60000
test_num = 10000
img_dim = (1, 28, 28)
img_size = 784
def _download(file_name):
file_path = dataset_dir + "/" + file_name
if os.path.exists(file_path):
return
print("Downloading " + file_name + " ... ")
urllib.request.urlretrieve(url_base + file_name, file_path)
print("Done")
def download_mnist():
for v in key_file.values():
_download(v)
def _load_label(file_name):
file_path = dataset_dir + "/" + file_name
print("Converting " + file_name + " to NumPy Array ...")
with gzip.open(file_path, 'rb') as f:
labels = np.frombuffer(f.read(), np.uint8, offset=8)
print("Done")
return labels
def _load_img(file_name):
file_path = dataset_dir + "/" + file_name
print("Converting " + file_name + " to NumPy Array ...")
with gzip.open(file_path, 'rb') as f:
data = np.frombuffer(f.read(), np.uint8, offset=16)
data = data.reshape(-1, img_size)
print("Done")
return data
def _convert_numpy():
dataset = {}
dataset['train_img'] = _load_img(key_file['train_img'])
dataset['train_label'] = _load_label(key_file['train_label'])
dataset['test_img'] = _load_img(key_file['test_img'])
dataset['test_label'] = _load_label(key_file['test_label'])
return dataset
def init_mnist():
download_mnist()
dataset = _convert_numpy()
print("Creating pickle file ...")
with open(save_file, 'wb') as f:
pickle.dump(dataset, f, -1)
print("Done!")
def _change_one_hot_label(X):
T = np.zeros((X.size, 10))
for idx, row in enumerate(T):
row[X[idx]] = 1
return T
def load_mnist(normalize=True, flatten=True, one_hot_label=False):
if not os.path.exists(save_file):
init_mnist()
with open(save_file, 'rb') as f:
dataset = pickle.load(f)
if normalize:
for key in ('train_img', 'test_img'):
dataset[key] = dataset[key].astype(np.float32)
dataset[key] /= 255.0
if one_hot_label:
dataset['train_label'] = _change_one_hot_label(dataset['train_label'])
dataset['test_label'] = _change_one_hot_label(dataset['test_label'])
if not flatten:
for key in ('train_img', 'test_img'):
dataset[key] = dataset[key].reshape(-1, 1, 28, 28)
return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label'])
# NN訓練程式碼
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_ laobel = True)
train_loss_list = []
train_acc_list = []
test_acc_list = []
# 平均每個epoch的重複次數
iter_per_epoch = max(train_size / batch_size, 1)
# 超引數
iters_num = 10000
batch_size = 100
learning_rate = 0.1
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
for i in range(iters_num):
# 獲取mini-batch
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 計算梯度
grad = network.numerical_gradient(x_batch, t_batch)
# grad = network.gradient(x_batch, t_batch) # 高速版!
# 更新引數
for key in ('W1', 'b1', 'W2', 'b2'): n
etwork.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
# 計算每個epoch的識別精度
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))
小節
這篇中介紹了NN的一些基礎知識,也給出了一個用numpy實現的十分簡單的一個2層神經網路的實現,將在下篇中介紹反向傳播法,對現在實現的神經網路進行更進一步的優化。
本文首發於我的知
