【2017cs231n】:課程筆記-第2講:影象分類
【2017cs231n】:課程筆記-第2講:影象分類
搜尋微信公眾號:'AI-ming3526'或者'計算機視覺這件小事' 獲取更多演算法、機器學習乾貨
csdn:https://blog.csdn.net/baidu_31657889/
github:https://github.com/aimi-cn/AILearners
課程簡介
斯坦福CS231n(面向視覺識別的卷積神經網路)課程大家都很熟悉了,深度學習入門必備課程。
這是一門每學期的視訊更新都會引起一波尖叫的明星課。我參照的是2017版。
課程資源
課程地址:http://cs231n.stanford.edu/
課程地址中文版-網易雲課程
課程地址中文版-b站
課程筆記github地址
課程ppt地址:關注公眾號“計算機視覺這件小事”或者“AI-ming3526” 回覆關鍵字“cs231n”免費獲取
課程作業
官方筆記作業地址:http://cs231n.github.io/
在寫筆記的過程中 我會尋找一下19年或者18年的課程作業來做一下 可能會有用到pytorch和tensorflow可以順便鍛鍊一下程式碼能力
section2.1 資料驅動方法
在上一講,提到了關於影象分類的任務,這是一個計算機視覺中真正核心的任務,同時也是本課程中關注的重點。
當做影象分類時,分類系統接收一些輸入影象,並且系統已經清楚了一些已經確定了分類或者標籤的集合,標籤可能是貓、狗、汽車以及一些固定的類別標籤集合等等;計算機的工作就是觀察圖片並且給它分配其中一些固定的分類標籤。對於人來說這是非常簡單的事情,但對計算機來說,卻是非常困難的事情。
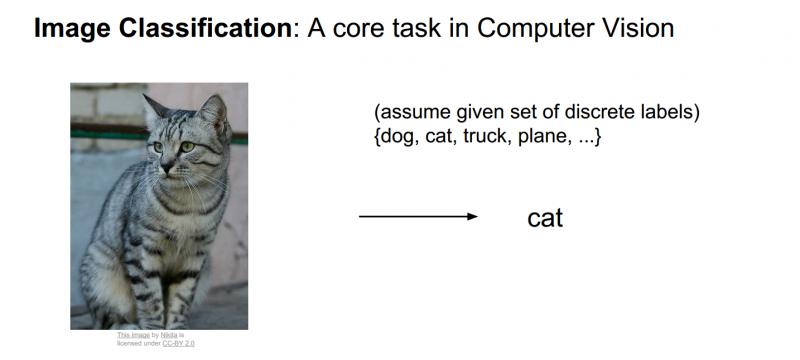
當一個計算機看這些圖片的時候,他看到的是什麼那,他肯定沒有一直貓咪的整個概念,而不像我們看到的一樣,計算機圖片的方式其實就是一大堆數字。所以影象大小(如上圖)可能是寬600畫素,高800畫素,有3個顏色通道,分別是紅、綠和藍(簡稱RGB)。如此,該影象就包含了600X800X3=1440000個數字,每個數字都是在範圍0-255之間的整型,其中0表示全黑,255表示全白。我們的任務就是把這些上百萬的數字變成一個簡單的標籤,比如“貓”。
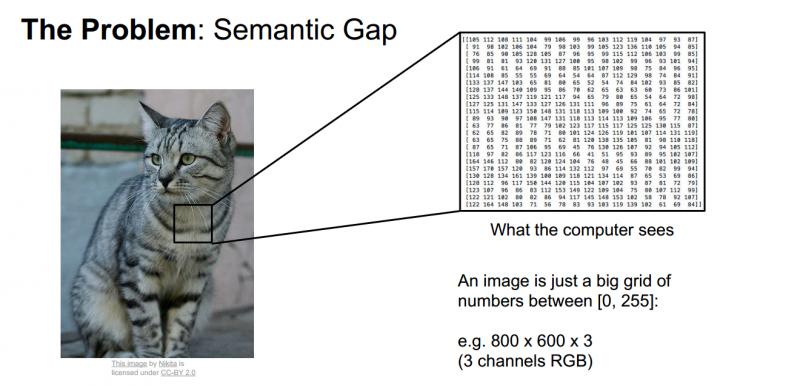
所以,對計算機來說,這就是一個巨大的數字陣列,很難從中提取出貓咪的特徵,我們把這個問題稱為“語義鴻溝”。對於貓咪的概念或者它的標籤,是我們賦予影象的一個語義標籤,而貓咪的語義標籤和計算機實際看到的畫素值之間有很大的差距。
困難和挑戰:對於人來說,識別出一個像“貓”一樣視覺概念是簡單至極的,然而從計算機視覺演算法的角度來看就值得深思了。我們在下面列舉了計算機視覺演算法在影象識別方面遇到的一些困難,要記住影象是以3維陣列來表示的,陣列中的元素是亮度值。
- 視角變化:同一個物體,攝像機可以從多個角度來展現。
- 大小變化:物體可視的大小通常是會變化的(不僅是在圖片中,在真實世界中大小也是變化的)。
- 形變:很多東西的形狀並非一成不變,會有很大變化。
- 遮擋:目標物體可能被擋住。有時候只有物體的一小部分(可以小到幾個畫素)是可見的。
- 光照條件:在畫素層面上,光照的影響非常大。
- 背景干擾:物體可能混入背景之中,使之難以被辨認。
- 類內差異:一類物體的個體之間的外形差異很大,比如椅子。這一類物體有許多不同的物件,每個都有自己的外形。
面對以上所有變化及其組合,好的影象分類模型能夠在維持分類結論穩定的同時,保持對類間差異足夠敏感。




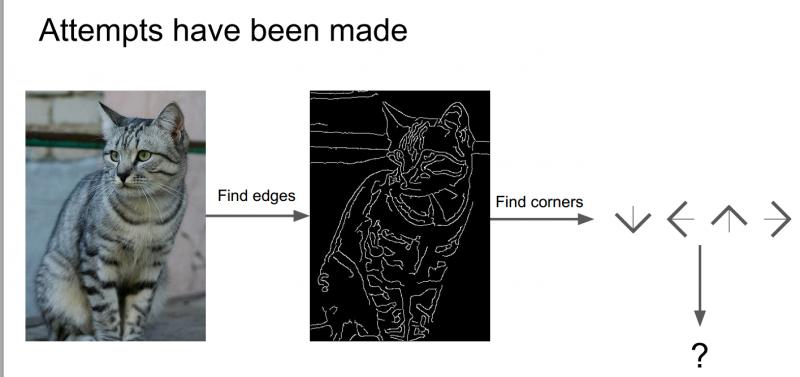
如果使用python寫一個影象分類器,定義一個方法,接受圖片作為輸入引數,來一波神操作,最終返回到圖片上進行標記是貓還是狗等等。但是並什麼簡單明瞭的演算法可以直接完成這些識別,所以影象識別演算法很難。

對於貓來說,它有耳朵、眼睛、鼻子、嘴巴,而通過上一章中Hubel和Wiesel的研究,我們瞭解到邊緣對於視覺識別是十分重要的,所以嘗試計算出影象的邊緣,然後把邊、角各種形狀分類好,可以寫一些規則來識別這些貓。
但是如果想識別比如卡車、其他動物等,又需要重新從頭再來一遍,所以這不是一種可推演的方法,我們需要的是一種識別演算法可以拓展到識別世界上各種物件,由此我們想到了一種資料驅動的方法。
我們並不需要具體的分類規則來識別一隻貓或魚等其他的物件,取而代之的方法是:
(1)首先收集不同類別圖片的示例圖,製作成帶有標籤的影象資料集;
(2)然後用機器學習的方法來訓練一個分類器;
(3)最後用這個分類器來識別新的圖片,看是否能夠識別。
所以,如果寫一個方法,可以定義兩個函式,一個是訓練函式,用來接收圖片和標籤,然後輸出模型;另一個數預測函式,接收一個模型,對圖片種類進行預測。

這種資料驅動類的演算法是比深度學習更廣義的一種理念,通過這種過程,最簡單的分類器(最近鄰分類器),在訓練過程中,我們只是單純的記錄所有的訓練資料;在預測過程中,拿新的影象與已訓練好的訓練對比,進行預測。
影象分類資料集:CIFAR-10。一個非常流行的影象分類資料集是CIFAR-10。這個資料集包含了60000張32X32的小影象。每張影象都有10種分類標籤中的一種。這60000張影象被分為包含50000張影象的訓練集和包含10000張影象的測試集。在下圖左側中你可以看見10個類的10張隨機圖片。

左邊:從CIFAR-10資料庫來的樣本影象。右邊:第一列是測試影象,然後第一列的每個測試影象右邊是使用Nearest Neighbor演算法,根據畫素差異,從訓練集中選出的10張最類似的圖片。
我們需要知道一個細節問題:給定兩幅圖片,該怎麼對它們進行比較?
如果將測試圖片和所有訓練圖片進行比較,將有很多不同的選擇來確定需要什麼樣的比較函式。我們可以使用L1距離(有時稱為曼哈頓距離),這是一個簡單的比較圖片的方法,只是對這些圖片中的單個畫素進行比較:
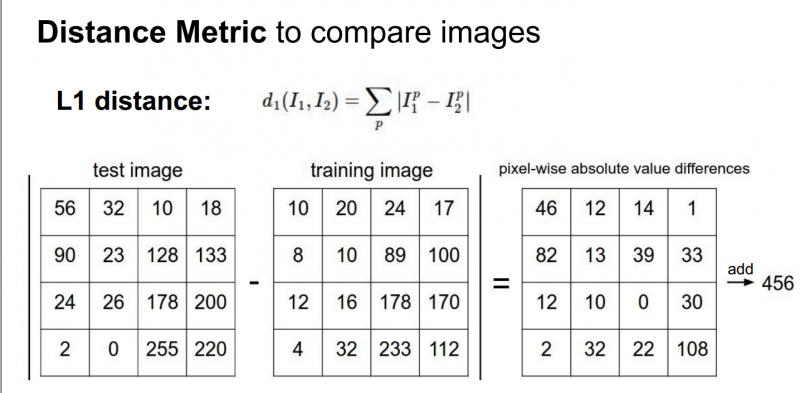

測試和訓練兩張圖片使用L1距離來進行比較。影象逐個畫素求差值,然後將所有差值加起來得到一個數值。如果兩張圖片一模一樣,那麼L1距離為0,但是如果兩張圖片很是不同,那L1值將會非常大。
雖然這個方法有些笨,但是有些時候卻有它的合理性,它給出了比較兩幅圖片的具體方法。
下面是最近鄰分類器的python程式碼


但是最近鄰演算法會出現下面的問題,如果我們在訓練集中有N個例項,訓練和測試的過程時間複雜度的情況那,答案是訓練:O(1) 測試:O(N),由此看來最近鄰演算法有點落後了,它在訓練中花的時間很少,而在測試中花了大量時間;而看卷積神經網路和其他引數模型,則正好相反,它們會花很多時間在訓練上,而在測試過程中則非常快。我們希望的是測試能夠更快一點,而訓練慢一點沒有關係,它是在資料中心完成的。
那麼在實際應用中,最近鄰演算法到底表現如何?可以看到下面的影象:
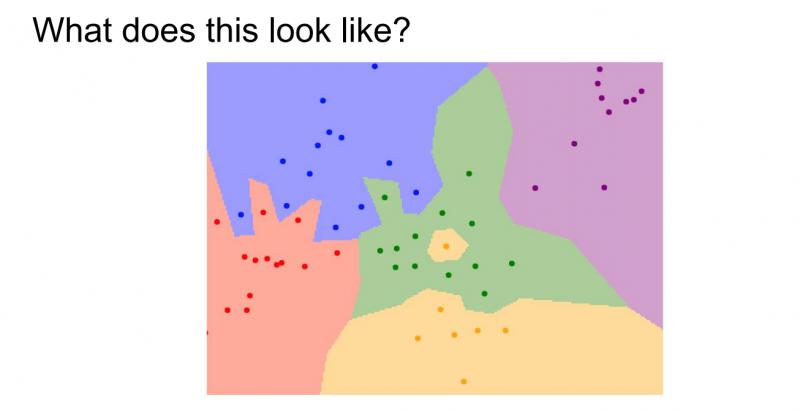

它是最近鄰分類器的決策區域,訓練集包含二維平面中的這些點,點的顏色代表不同的類別或不同的標籤,這裡有五種型別的點。對於這些點來說,將計算這些訓練資料中最近的例項,然後在這些點的背景上著色,標示出它的類標籤,可以發現最近鄰分類器是根據相鄰的點來切割空間並進行著色。
但是通過上述圖片中,可以看到綠色區域中間的黃色區域(事實上該點應該是綠色的),藍色區域中有綠色區域的一部分,這些都說明了最近鄰分類器的處理是有問題的。
那麼,基於以上問題,產生了K-近鄰演算法,它不僅是尋找最近的點,還會做一些特殊的操作,根據距離度量,找到最近的K個點,然後在這些相鄰點中進行投票,票數多的近鄰點預測出結果。
下面用同樣的資料集分別使用K=1、K=3、K=5的最近鄰分類器:


在K=3時,可以看到綠色區域中的黃色點不再會導致周圍的區域被劃分成黃色,因為使用了多數投票,中間的這個綠色區域都會被劃分成綠色;在K=5時,可以看到藍色和紅色區域間的決策邊界變得更加平滑好看。
所以使用最近鄰分類器時,總會給K賦一個比較大的值,這會是決策邊界變得更加平滑,從而得到更好的結果。當然這個值也不能太大,要在你測試或者訓練樣本的大小上調整。
之前寫過的一個機器學習實戰的k-近鄰演算法例子-識別手寫數字:https://blog.csdn.net/baidu_31657889/article/details/89095213
學生提問:上圖中白色區域代表什麼?
答:白色區域表示這個區域沒有獲得K-最近鄰的投票,可以做大膽的假設,把它劃分為一個不同的類別。
section2.2 K-近鄰演算法
繼續討論KNN(K-最近鄰演算法),回到圖片中來,它實際表現的並不好,用紅色和綠色分別標註了影象分類的正確與否:


取決於它的近鄰值,可以看到KNN的表現效果不是很好,但如果可以使用一個更大的K值,那麼投票操作的結果就可能會達到很好的分類效果。
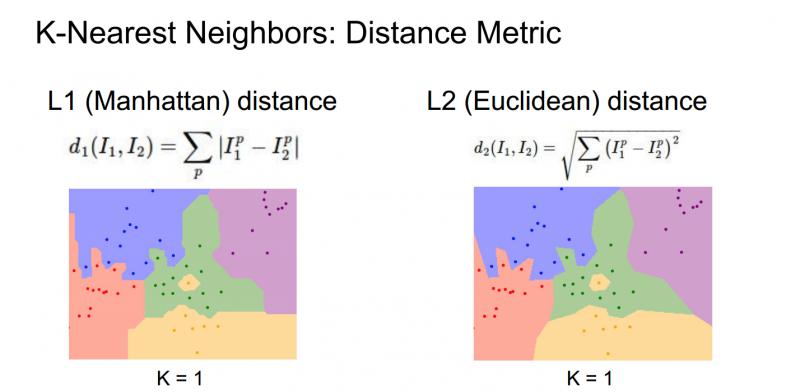
當我們使用K-最近鄰演算法時,確定應該如何比較相對近鄰資料距離值。比如,已經討論過的L1距離,它是畫素之間絕對值的總和;另一種常見的選擇是L2距離,也就是歐式距離(平方和的平方根)。
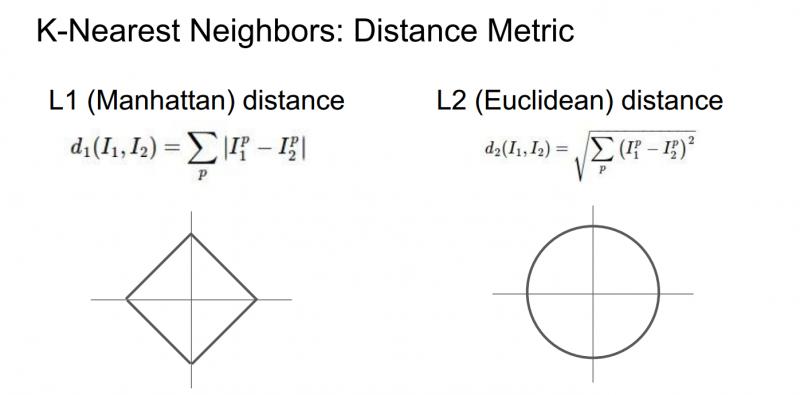

這兩種方式,L1取決於你選擇的座標系統,所以如果轉動座標軸,將會改變點之間的L1距離;而改變座標軸對L2距離無影響。
下面不同距離的決策邊界的形狀變化很大,L1中這些決策邊界趨於跟隨座標軸,又是因為L1取決於我們選擇的座標系,L2對距離的排序不會受到座標軸的影響,只是吧邊界放置在最自然的地方。(好吧,我竟然看不出來太大區別==) 但是 http://vision.stanford.edu/teaching/cs231n-demos/knn/ 這個網站上的效果真的很明顯,大家去看看,顯然使用L2歐氏距離對擬合效果更好,邊緣更加自然,這個KNN,實際上是非常有趣的,可以很好地培養決策邊界的直覺。

所以,一旦真的嘗試在實踐中使用這個演算法,有幾個選擇是需要做的。比如,討論過的選擇K的不同值,選擇不同的距離度量,該如何根據問題和資料來選擇這些超引數,K值和距離度量稱之為超引數,它們不一定能從訓練資料中學到。
在實際中,大多使用k-NN分類器。但是k值或者說這些超引數如何確定呢?
錯誤的兩種想法 Idea1 and Idea2
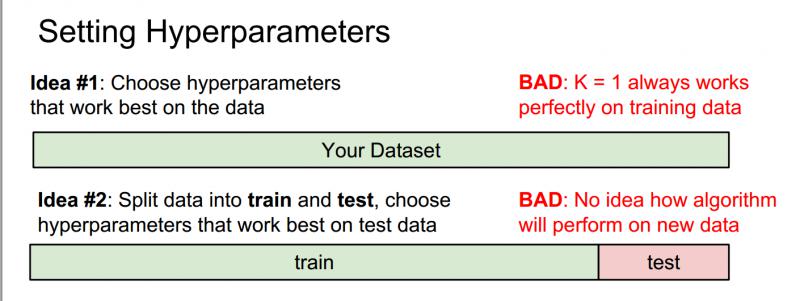

(1)選擇能對訓練集給出最高的準確率、表現最佳的超引數;
不要這麼做,在機器學習中,不是要儘可能擬合訓練集,而是要讓分類器在訓練集以外的未知資料上表現更好。如在k最近鄰演算法中,假設k=1,我們總能完美的分類訓練集資料,在實踐中,讓k取更大的值,儘管會在訓練集中分錯個別資料,但對於訓練集中未出現過的資料分類效能更佳。
(2)所有的資料分成兩部分:一部分是訓練集,另一部分是測試集,然後在訓練集上使用不同的超引數來訓練演算法,將訓練好的分類器用在測試集上,再選擇一組在測試集上表現最好的超引數;
同樣不要這麼做,機器學習系統的目的是讓我們瞭解演算法表現究竟如何,所以測試集的目的是給我們一種預估方法,如果採用這種方法,只能讓我們演算法在這組測試集上表現良好,但它無法代表在未見過的資料上的表現。
正確的兩種想法 Idea3 Idea4



(3)所有資料分成三部分:訓練集、驗證集和測試集,大部分資料作為訓練集,通常所做的是在訓練集上用不同的超引數來訓練演算法,在驗證集上進行評估,然後用一組超參選擇在驗證集上表現最好的,再把這組驗證集上表現最好的分類器拿出來在測試集上執行,這才是正確的方法。
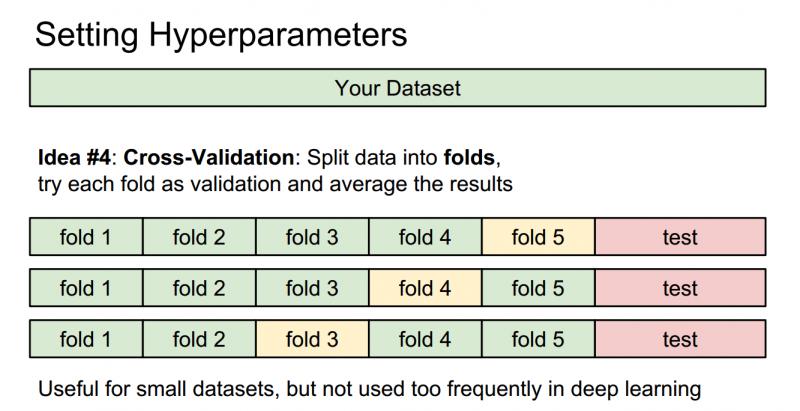
(4)交叉驗證:在深度學習中不太常見。有時候,訓練集數量較小(因此驗證集的數量更小),這種方法更加複雜些。還是用剛才的例子,如果是交叉驗證集,我們就不是取1000個影象,而是將訓練集平均分成5份,其中4份用來訓練,1份用來驗證。然後我們迴圈著取其中4份來訓練,其中1份來驗證,最後取所有5次驗證結果的平均值作為演算法驗證結果。
那麼經過交叉驗證可能會得到這樣的一張圖:
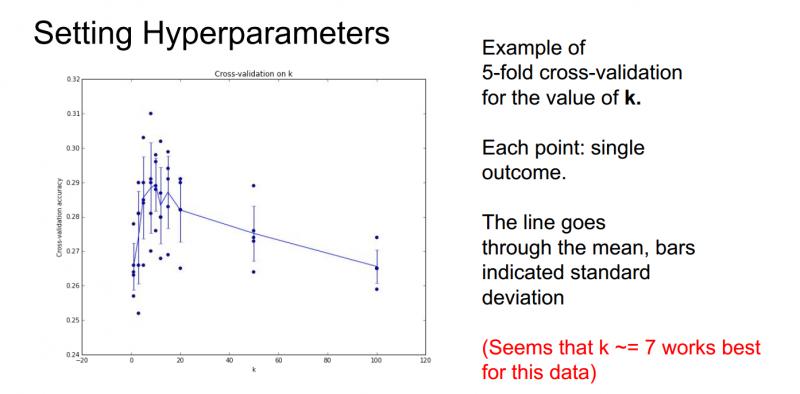

橫軸表示K-近鄰分類器中的引數K值,縱軸表示分類器對不同K值在資料上的準確率。這裡用了5折交叉驗證,對每個K值,都對演算法進行了5次不同的測試來了解這個演算法表現如何;所以當訓練一個機器學習的模型時,最後要畫這樣一張圖,從中可以看出演算法的表現以及各個超引數之間的關係,最終可以選出在驗證集上最好的模型以及相應的超引數。
其實,KNN在影象分類中很少用到。
(1)它的測試時間非常長
(2)像歐式距離或者L1距離這樣的衡量標準用在比較影象上不太合適,這種向量化的距離函式不太適合表示影象之間視覺的相似度
究竟我們是如何區分影象不同呢?


最左邊是最原始的圖片,右邊是經過處理的圖片,如遮住嘴,向下平移幾個畫素的距離,或者把整幅圖染的偏藍,如果計算原圖和遮擋的圖、平移、染色的圖之間的歐幾里得距離,結果是一樣的,L2確實不適合表示影象之間視覺感知的差異。
為什麼L2的距離是一樣的,原因是我們在處理的時候故意這樣做成原圖和這些圖計算L2距離相同,這樣就可以顯示L2距離甚至KNN都不適合影象之間的計算。
(3)維度災難:KNN有點像把樣本空間分成幾塊,意味著如果希望分類器有好的效果,需要訓練資料密集的分佈在空間中;而問題在於,想要密集的分佈在樣本空間中,需要指數倍的訓練資料,然而不可能拿到這樣高維空間中的畫素。
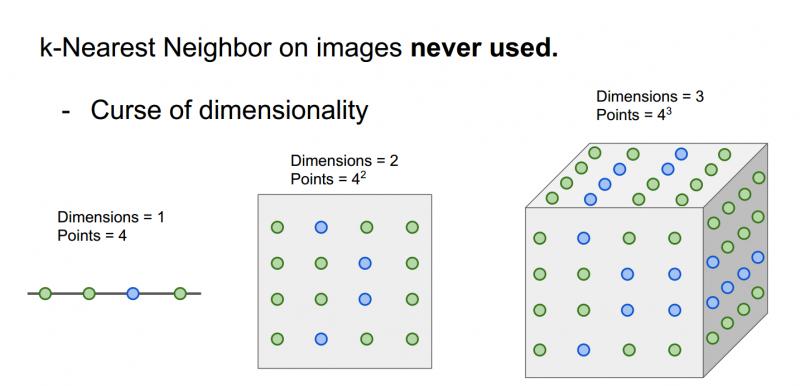

注意:這裡的點是表示訓練資料,點的顏色代表他們的類別。在一維空間,兩個類別只需要4個點就可以把空間覆蓋,二維空間的話就需要16個點,三維需要64個點,訓練樣本的個數是指數增長的,很恐怖。
KNN:總結
在 影象分類 中,我們從一組 訓練資料集 的影象和標籤開始,並且必須預測 測試集 上的標籤
k近鄰分類器 基於最近的訓練例項預測標籤
距離度量(L1 L2)和K是 超引數
使用 驗證集 選擇超引數;我們的測試集要放到最後執行,而且只執行一次。
section2.3 線性分類
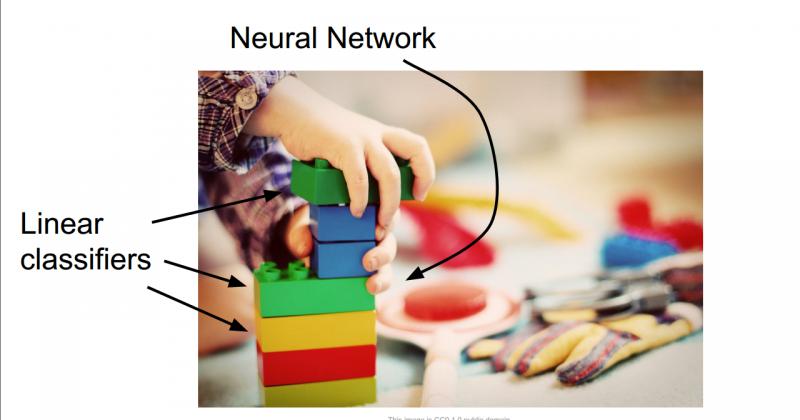
線性分類非常重要,同時它也是一個相對簡單的學習演算法,這有助於我們建立起來整個神經網路和卷積網路。
線性分類就例如,你在玩樂高玩具的時候,搭出來的整個大的城堡或者什麼東西相當於整個神經網路,而線性分類器就相當於整個樂高城堡的基礎模組。

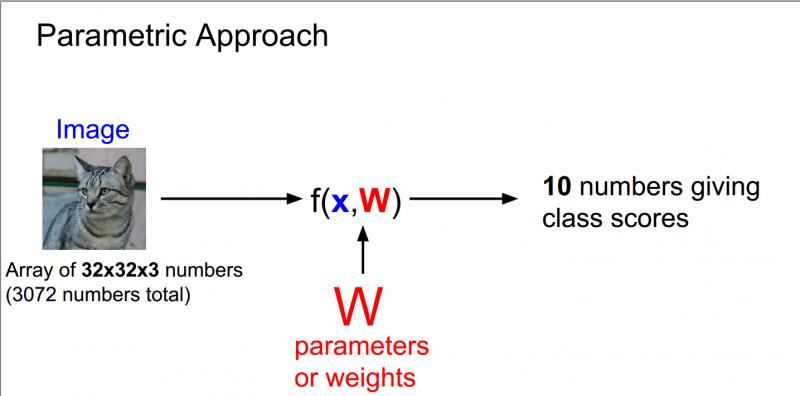
線上性分類中,將採用與K-最近鄰稍有不同的方法,線性分類是引數模型中最簡單的例子,以下圖為例,我們使用的還是CIFAR10資料集,裡面10個類別,每個影象大小為32 * 32 * 3。

上圖中32 * 32 * 3中3指的是RGB三通道,因為是彩色影象所以有三個通道,而灰色影象是二維的。
通常把輸入資料設為x,權重設為w,現在寫一些函式包含了輸入引數x和引數w,然後就會有10個數字描述的輸出,即在CIFAR-10中對應的10個類別所對應的分數。 現在,在這個引數化的方法中,我們總結對訓練資料的認知並把它都用到這些引數w中,在測試的時候,不再需要實際的訓練資料,只需要這些引數來預測結果,這使得模型更有效率。
在深度學習中,整個描述都是關於函式F正確的結構,可以來編寫不同的函式形式用不同的、複雜的方式組合權重和資料,這些對應於不同的神經網路體系結構,將他們相乘是最簡單的組合方式,這就是一個線性分類器。
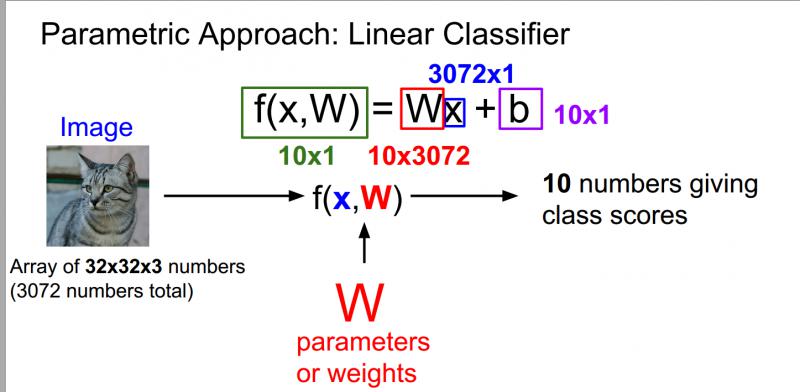

用自己的語言解釋一下上圖:最左邊的貓是輸入的影象,就相當於中間公式的X,輸入影象大小是32 * 32 * 3一共是展開是3072 * 1的列向量,W我們可以把他相當於一個權重矩陣,他的作用就是記錄我們在深度學習學習到的東西,在測試的時候只需要W矩陣就可以預測結果,W的大小是10 * 3072,W和X相乘之後,就會得到一個列向量,剛好是10 * 1,就對應最後十個分類的值,哪個分類的值最大,我們就認定這個影象的分類是那一類。有時候也會加上b,這是一個偏置項,他是給我們一些資料獨立的偏好值,針對僅僅一類的偏好值。
線性分類器工作的例子如下:
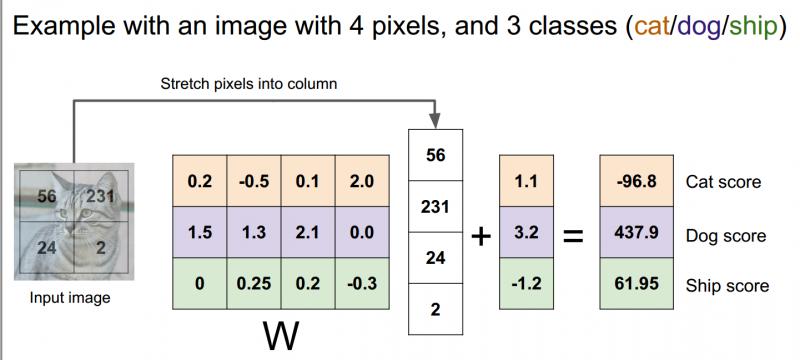

我們把2*2的影象拉伸成一個有4個元素的列向量,在這個例子中,只限制了3類:貓,狗,船;權重矩陣w是3行4列(4個畫素3個類);加上一個3元偏差向量,它提供了每個類別的資料獨立偏差項;現在可以看到貓的分數是影象畫素和權重矩陣之間的輸入乘積加上偏置項。
下圖是我們已經訓練好的一個線性分類器,最下方是我們資料集中訓練得到的權重矩陣中的行向量對應於10個類別相關的視覺化結果。


線性分類器的另一個觀點是迴歸到影象,作為點和高維空間的概念,可以想像每一張影象都是類似高維空間中的一個點,現線上性分類器嘗試線上性決策邊界上畫一個線性分類面來劃分一個類別和剩餘其他類別,如下圖所示:
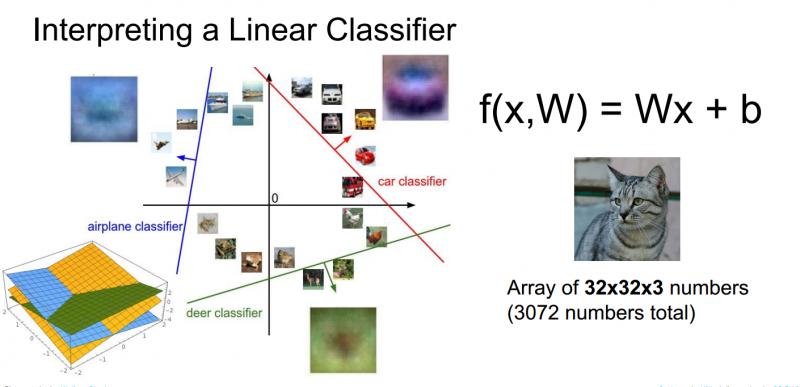

在訓練過程中,這些線條會隨機地開始,然後快速變化,試圖將資料正確區分開,但是從這個高維的角度考慮線性分類器,就能再次看到線性分類器中出現的問題。
假設有一個兩類別的資料集,藍色和紅色,藍色類別是影象中畫素數量大於0且都是奇數;紅色類別是影象中畫素數量大於0且都是偶數,如果去畫這些不同的決策,能看到奇數畫素點的藍色類別在平面上有兩個象限,所以沒有辦法能夠繪製一條單獨的直線來劃分藍色和紅色,這就是線性分類器的問題所在。如下圖最左邊。
當然線性分類器還有其他難以解決的情況,比如多分類問題,如下圖所示中間和最右邊。
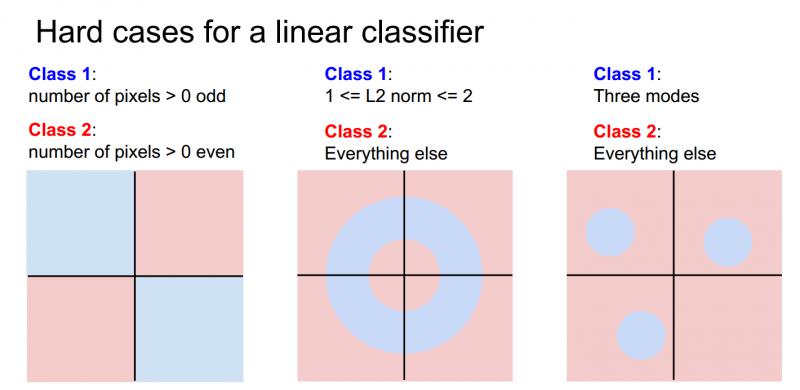

因此,線性分類器的確存在很多問題,但它是一個非常簡單的演算法,易於使用和理解。
總結:
本節中討論了線性分類器對應的函式形式(矩陣向量相乘),對應於模版匹配和為每一類別學習一個單獨的模板,一旦有了這個訓練矩陣,可以用他得到任何新的訓練樣本的得分。
思考問題:如何給資料集選擇一個正確的權重?這裡包括損失函式和一些其他的優化方法,將在下一章中繼續討論。
AIMI-CN AI學習交流群【1015286623】 獲取更多AI資料
分享技術,樂享生活:我們的公眾號計算機視覺這件小事每週推送“AI”系列資訊類文章,歡迎您的關注
