GCN和GCN在文字分類中應用
1.GCN的概念
傳統CNN卷積可以處理圖片等歐式結構的資料,卻很難處理社交網路、資訊網路等非歐式結構的資料。一般圖片是由c個通道h行w列的矩陣組成的,結構非常規整。而社交網路、資訊網路等是圖論中的圖(定點和邊建立起的拓撲圖)。
傳統CNN卷積面對輸入資料維度必須是確定的,進而CNN卷積處理後得到的輸出資料的維度也是確定的。歐式結構資料中的每個點周邊結構都一樣,如一個畫素點周圍一定有8個畫素點,即每個節點的輸入維度和輸出維度都是固定的。而非歐式結構資料則不一定,如社交網路中A和B是朋友,A有n個朋友,但B不一定有n個朋友,即每個節點的輸入維度和輸出維度都是不確定的。
所以不能使用CNN來對社交網路、資訊網路等資料進行處理,因為對A節點處理後得到輸出資料的維度和對B節點處理後得到輸出資料維度是不一樣的。為了得到社交網路、資訊網路的空間特徵所以我們使用GCN(Graph Convolutional Network)來處理。
2. GCN工作原理

圖1 一個GCN的例項(圖片來源網頁[3])
同一般的卷積神經網路不同,GCN輸入的資料是一個圖拓撲矩陣,這個拓撲矩陣一般是圖的鄰接矩陣。
2.1 概念定義
| 概念 | 定義 |
|---|---|
| G | 一個拓撲圖定義為G=(V,E) 其中V是節點集合,E是邊集合。 |
| N | N是圖中節點個數,即|V| |
| F | 節點的特徵數,不同學習任務F不同 |
| X | 網路初始化矩陣, X是N行F列的矩陣 |
| D | 圖的度矩陣,Dij表示點i和點j是否存在連線 |
| A | 圖結構表徵矩陣, A是N行N列的矩陣,A通常是G的鄰接矩陣 |
| Hi | GCN中每層輸出矩陣 Hi是一個N行F列矩陣 |
| Wi | GCN中每層權值矩陣 Wi是一個F行F列矩陣 |
2.2 GCN計算方式
在GCN中,第1層又H0 = X,從i層到i+1層網路計算其中一個簡單傳播規則,即傳播規則1:
\[\begin{array}{l} {{\bf{H}}^{i + 1}} = f\left( {{{\bf{H}}^i},{\bf{A}}} \right) \\ \quad \;\;\; = \sigma \left( {{\bf{A}}{{\bf{H}}^i}{{\bf{W}}^i}} \right) \\ \end{array}\]
其中啟用函式σ一般為ReLu函式。盡然這個規則下GCN是一個簡單模型,但已經足夠強大,當然實際使用傳播規則是下面幾個:
傳播規則2
\[\begin{array}{l}
{{\bf{H}}^{i + 1}} = f\left( {{{\bf{H}}^i},{\bf{A}}} \right) \\
\quad \;\;\; = \sigma \left( {{{\bf{D}}^{ - \frac{1}{2}}}{\bf{A}}{{\bf{D}}^{ - \frac{1}{2}}}{{\bf{H}}^i}{{\bf{W}}^i}} \right) \\
\end{array}\]
傳播規則3
\[\begin{array}{l}
{{\bf{H}}^{i + 1}} = f\left( {{{\bf{H}}^i},{\bf{A}}} \right) \\
\quad \;\;\; = \sigma \left( {\left( {{\bf{I}} + {{\bf{D}}^{ - \frac{1}{2}}}{\bf{A}}{{\bf{D}}^{ - \frac{1}{2}}}} \right){{\bf{H}}^i}{{\bf{W}}^i}} \right) \\
\end{array}\]
傳播規則4
\[\begin{array}{l} {{\bf{H}}^{i + 1}} = f\left( {{{\bf{H}}^i},{\bf{A}}} \right) \\ \quad \;\;\; = \sigma \left( {{{\bf{D}}^{ - \frac{1}{2}}}\left( {{\bf{D}} - {\bf{A}}} \right){{\bf{D}}^{ - \frac{1}{2}}}{{\bf{H}}^i}{{\bf{W}}^i}} \right) \\ \end{array}\]
傳播規則5
\[\begin{array}{l}
{{\bf{H}}^{i + 1}} = f\left( {{{\bf{H}}^i},{\bf{A}}} \right) \\
\quad \;\;\; = \sigma \left( {{{{\bf{\hat D}}}^{ - \frac{1}{2}}}{\bf{\hat A}}{{{\bf{\hat D}}}^{ - \frac{1}{2}}}{{\bf{H}}^i}{{\bf{W}}^i}} \right) \\
\end{array}\]
其中\({\bf{\hat A}}{\rm{ = }}{\bf{A}}{\rm{ + }}{\rm I}\),I是一個N×N的單位矩陣。而\({\bf{\hat D}}\)是\({\bf{\hat A}}\)
是一個對角線矩陣,其中${{\bf{\hat D}}{ii}} = \sum\limits_j {{{{\bf{\hat A}}}{ij}}} $。
最後根據不同深度學習任務來定製相應的GCN網路輸出。
3 GCN在文字分類中的應用
3.1 文字分類常用演算法
文字分類是自然語言處理比較常見的問題,常見的文字分類主要基於傳統的cnn、lstm以及最近幾年比較熱門的transform、bert等方法,傳統分類的模型主要處理排列整齊的矩陣特徵,也就是很多論文中提到的Euclidean Structure,但是我們科學研究或者工業界的實際應用場景中,往往會遇到非Euclidean Structure的資料,如社交網路、資訊網路,傳統的模型無法處理該類資料,提取特徵進一步學習,因此GCN 應運而生,本文主要介紹GCN在文字分類中的應用。
3.2 GCN在文字分類中具體應用
首先我們將我們的文字語料構建拓撲圖,改圖的節點由文件和詞彙組成,即圖中節點數|v|=|doc|+|voc| 其中|doc|表示文件數,|voc|表示詞彙總量,對於特徵矩陣X,我們採用單位矩陣I表示,即每個節點的向量都是one-hot形式表示,下面我們將介紹如何定義鄰接矩陣A,其公式如所示,對於文件節點和詞彙節點的權重,我們採用TF-IDF表示,對於詞彙節點之間的權重,我們採用互資訊表示(PMI, point-wise mutual information),在實驗中,PMI表現好於兩個詞彙的共現詞彙數,其公式如所示:
\[{A_{ij}} = \left\{ \begin{array}{l}
{\rm{PMI}}\left( {i,j} \right)\quad \quad \quad \quad i和j是詞語而且{\rm{PMI}}\left( {i,j} \right) > {\rm{0}} \\
{\rm{TF - IDF}}\left( {i,j} \right)\quad \;\;i是文件j是詞語 \\
1\quad \quad \quad \quad \quad \quad \quad \;\;\;i = j \\
0\quad \quad \quad \quad \quad \quad \quad \;\;其他\\
\end{array} \right.\]

其中#W(i)表示在固定滑動視窗下詞彙i出現的數量,#W(i, j)表示在固定滑動視窗下詞彙i,j同時出現的數量,當PMI(i, j)為正數表示詞彙i和詞彙j有較強的語義關聯性,當PMI(i, j)為負數的時候表示詞彙i,j語義關聯性較低,在構建完圖後,我們代入GCN中,構建兩層GCN,如下:

我們採用經典的交叉熵來定義損失函式:

其中YD表示帶標籤的文擋集合,Ydf 表示標註類別,Zdf為預測的類別。
下面介紹GCN在多個公開資料集上的實驗結果,其中資料來源為:

GCN在文字分類上的實驗結果見表2。
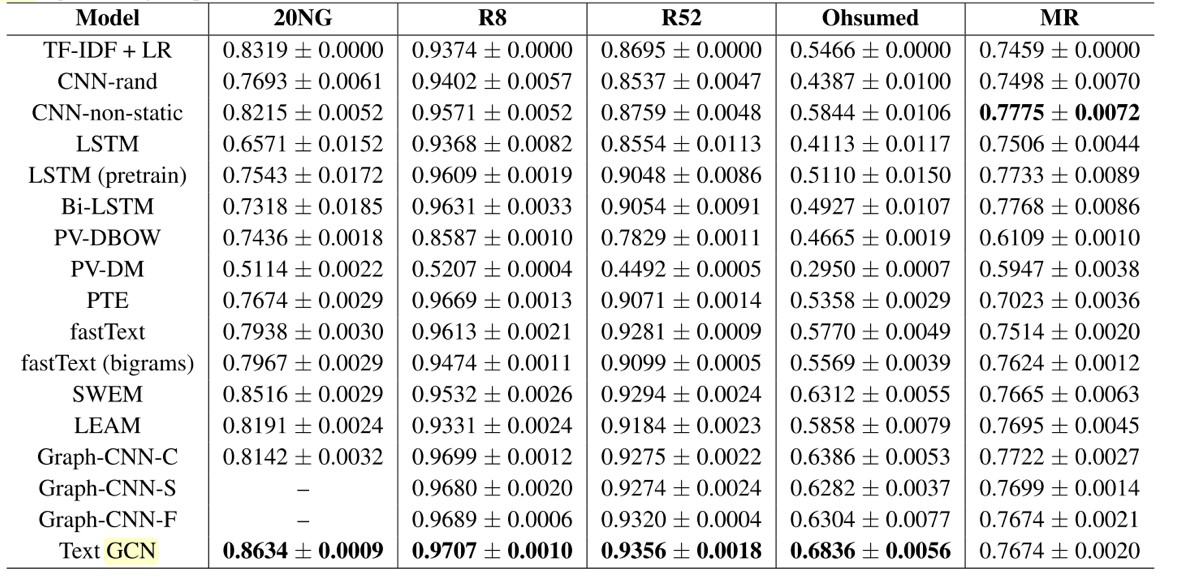
這種新穎的文字分類方法稱為文字圖卷積網路(Text-GCN),巧妙地將文件分類問題轉為圖節點分類問題。Text-GCN可以很好地捕捉文件地全域性單詞共現資訊和利用好文件有限地標籤。一個簡單的雙層Text-GCN已經取得良好地成果。
參考文獻
[1] Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv:1609.02907, 2016.
[2] Yao L, Mao C, Luo Y. Graph convolutional networks for text classification[J]. arXiv preprint arXiv:1809.05679, 2018.
[3] http://tkipf.github.io/graph-convolutional-networ
