【強化學習】階段總結
馬爾可夫決策過程 MDP
-
基於模型的動態規劃方法(Model-Based,DP)
-
策略搜尋
-
策略迭代
-
值迭代
-
-
無模型的強化學習方法(Model-Free)
-
蒙特卡洛方法(MC):效率不高,但是能夠展現 model-free 類演算法的特性;
-
時序差分方法(TD,Important):直接從 episode 學習,不需要了解模型本身,即 model-free;可以學習不完整的 episode,通過自身的引導(bootstrapping),猜測 episode 的結果,同時持續更新這個猜測;
TD vs. MC
-
MC 沒有偏差(Bias),但是有著較高的方差(Variance)
-
更好的收斂性質
-
對初始值不太敏感
-
使用簡單
-
-
TD 較低的方差,但是有一定程度的偏差
-
通常比 MC 更加高效
-
TD(0) 收斂到 Vπ(s)
-
對初始值更加敏感
-
MC 演算法試圖收斂至一個能夠最小化狀態價值與實際收穫的均方差的解決方案;
TD 演算法收斂到一個根據已有經驗構建的最大可能的馬爾可夫模型的狀態價值,也就是說 TD 演算法首先根據已有經驗估計狀態空間的轉移概率,同時估計某一個狀態的即時獎勵,最後計算該 MDP 的狀態函式。
換句話說:
MC 方法並不利用馬爾可夫性質,故在非馬爾可夫環境中更有效率;
TD(0) 利用馬爾可夫性質,在馬爾可夫環境中更有效率。
總結以上內容:
| Monte-Carlo | Temporal Difference |
| 要等到 episode 結束才能獲得 return | 每一步執行完都能獲得一個return |
| 只能使用完整的 episode | 可以使用不完整的 episode |
| 高方差,零偏差 | 低方差,有偏差 |
| 沒有體現出馬爾可夫性質 | 體現出了馬爾可夫性質 |
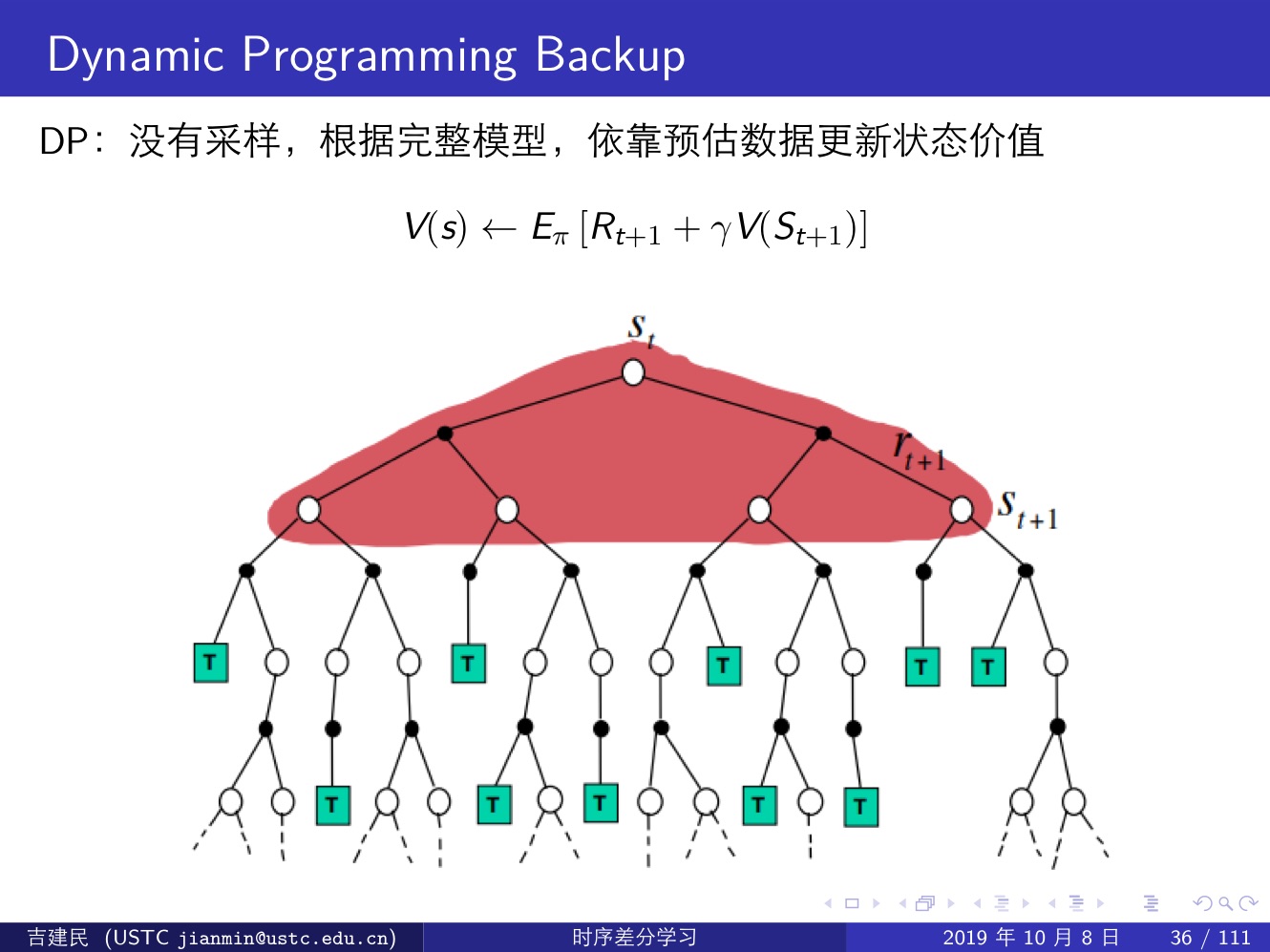
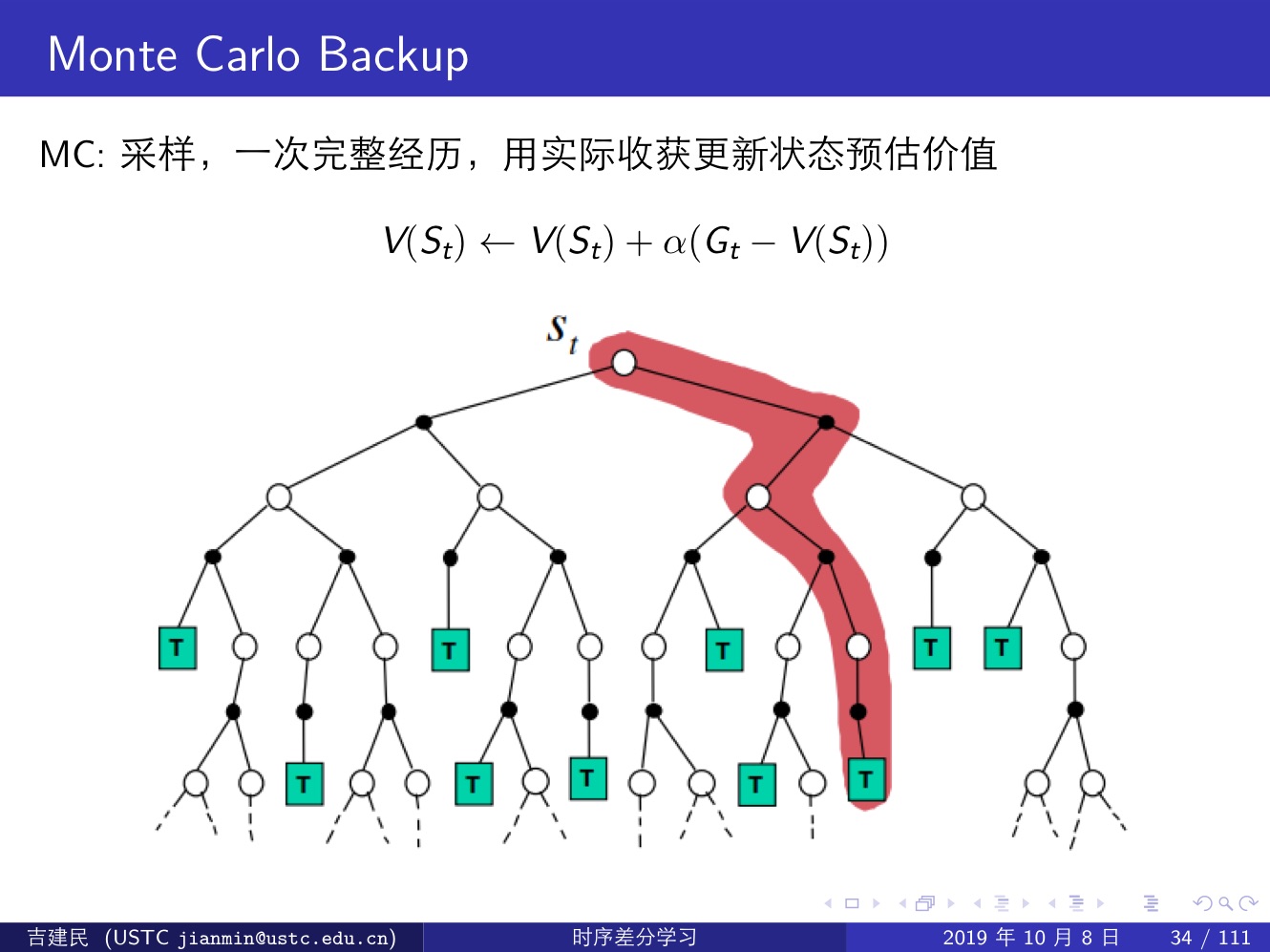
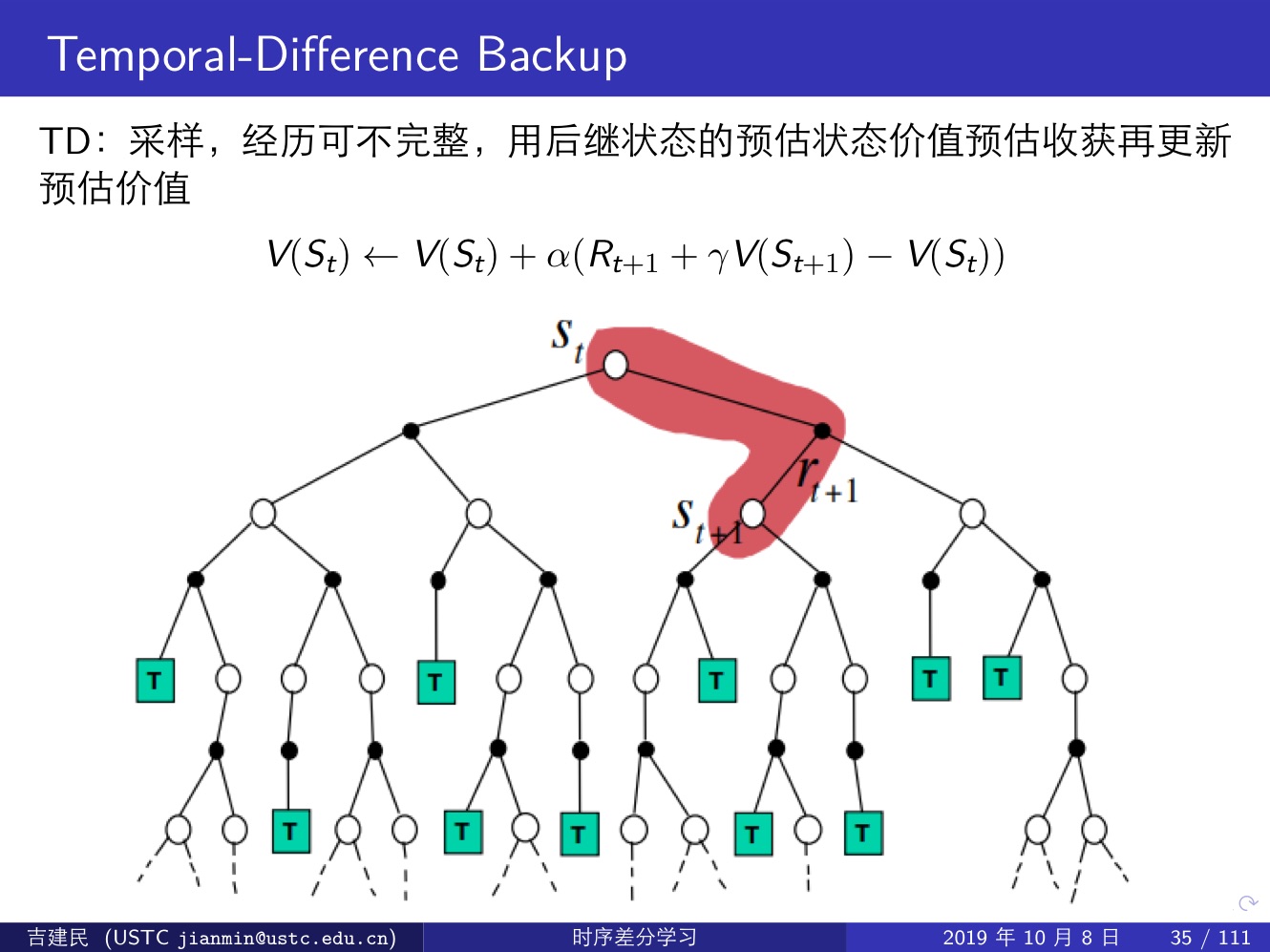
三種強化學習方法:Monte-Carlo,Temporal-Difference 和 Dynamic Programming,前兩種屬於 Model-Free 類方法(這其中 MC 需要一個完整的 episode,TD 則不需要完整的 episode),最後一種屬於 Model-Based 類方法,它通過計算一個狀態 s 所有可能的轉移狀態 s′ 及其轉移概率以及對應的即時獎勵來計算這個狀態 s 的價值
- 關於是否 Bootstrap:MC 沒有引導資料,只使用實際收穫;DP 和 TD 都有引導資料;
- 關於是否用樣本來計算:MC 和 TD 都是應用樣本來估計實際的價值函式;而 DP 則是利用模型直接計算得到實際價值函式,沒有樣本或者取樣之說。
- MC 方法使用值函式最原始的定義,該方法利用所有回報的累積和估計值函式;DP 方法和 TD 方法則利用一步預測方法計算當前狀態值函式。其共同點是利用了 bootstrapping 方法,不同的是,DP 方法利用模型計算後繼狀態,而 TD 方法利用試驗得到後繼狀態。
下面幾張提很好的說明了這三類演算法的區別:
強化學習大一統:
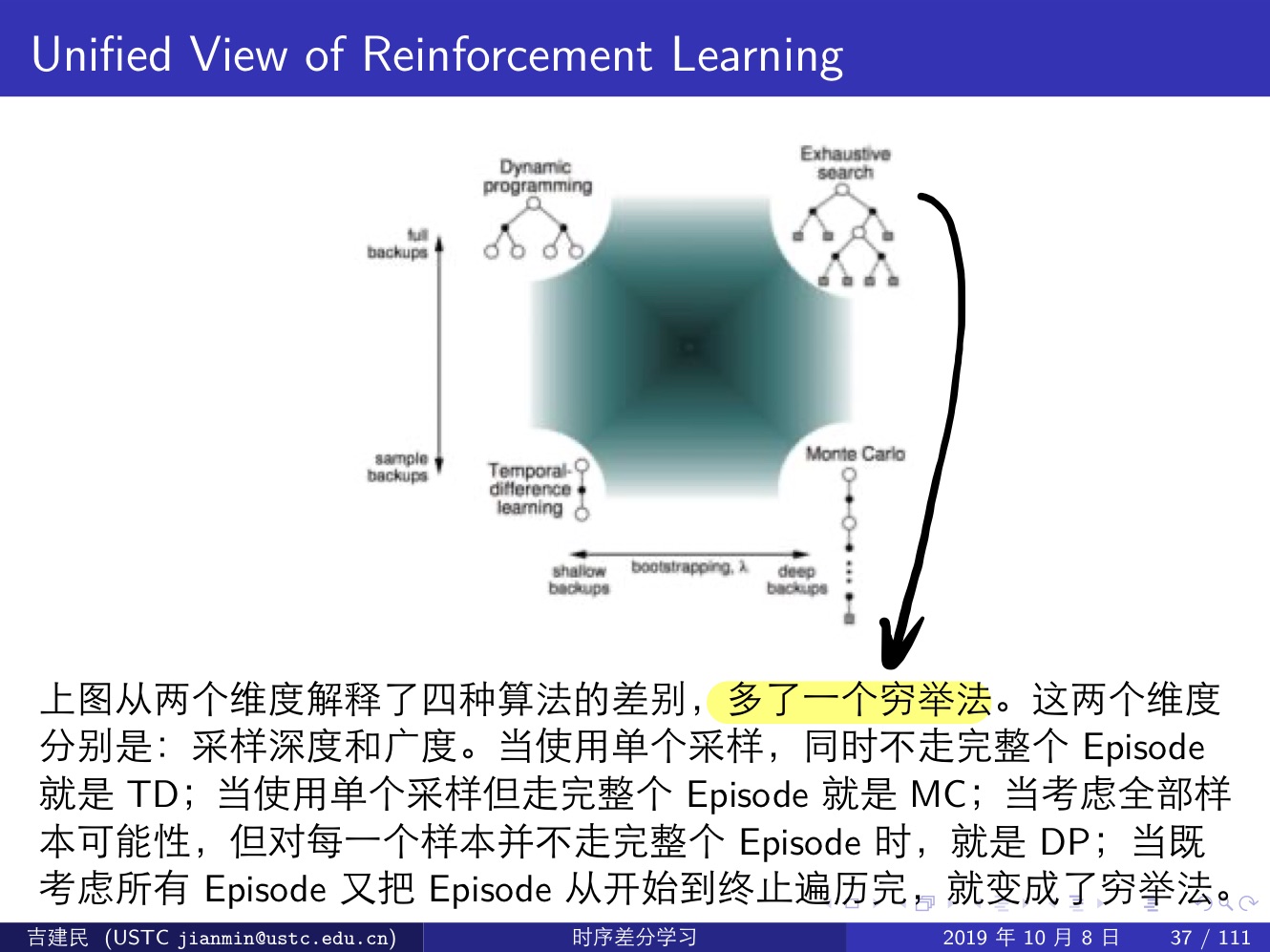
我們可以發現,MC 和 TD 方法都過於極端:
- MC 方法需要 episode 走到終止狀態才能更新,相當於 ∞-step TD target;
- TD 方法只走一步就更新,相當於 1-step TD target
通常好的方法都是在兩個極端之間進行選擇,也就是 n-step TD target,這要等到下次才寫了。
&n
