基於圖的半監督學習

以一個無標籤資料的例子作為墊腳石

        Alice正在翻閱一本《Sky and Earth》的雜誌，裡面是關於天文學和旅行的文章。Alice不會英文，她只能通過文章中的圖片來猜測文章的類別。比如第一個故事是“Bridge Asteroid”有一張多坑的小行星圖片，那麼它很明顯是天文學類別的。第二個故事是“Yellowstone Camping”有張灰熊的圖片，那麼將它分類到旅行類別。但是其它文章沒有圖片，Alice不能給它們分類。Alice是一個聰明的人，她注意到其他文章的標題“Asteroid and Comet,” “Comet Light Curve,” “Camping in Denali,” and “Denali Airport.”她猜測如果兩個文章的標題中有相同的單詞，它們可能是一個類的，然後他就畫出這樣一幅圖：

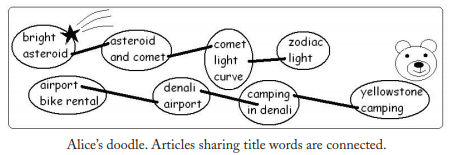
        這其實就是基於圖的半監督學習的一個例子。

圖的概念

        我們首先來看看如何從訓練資料中構建出圖，給定半監督資料集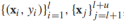 ，每個資料樣本（有標籤&無標籤）是圖上的一個頂點，顯然，圖會非常大，因為無標籤資料很多，一旦圖構建完成，學習的過程就包括給圖中的每一個定點設定標籤y值。在圖中可以通過邊將有標籤和無標籤資料點相連，邊通常是無向的，表示的是兩個節點（樣本）之間的相似性。將邊權重記作wij，wij越大，xi和xj越相似，兩者的標籤越可能相同。所以邊權重非常重要，人們常常將邊的權值定義為如下形式：

• 全連線圖：

　　每一對定點之間都有邊相連，邊的權重隨歐式距離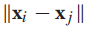 的增加而降低，常用的權重方程如下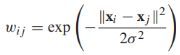： ，σ叫做頻寬引數用來控制權重衰減的速度。這個權重方程和高斯方程的形式相同，也叫做高斯核或者徑向基函式；

• KNN圖：

　　每一個定點定義它的歐式距離上的最近鄰，注意，如果xi在xj的k近鄰內，xj不一定在xi的k近鄰內，如果xi,xj中有一個在對方的k近鄰內我們就用邊將它們連線，這就意味著一個定點可能會有超過k條邊，如果xi,xj有邊相連，邊的權重wij就是1，否則為0。KNN圖可以自適應地適應樣本在特徵空間的密度（密集區KNN範圍的半徑小）；

• εNN圖：

　　將距離小於ε的頂點連一條邊。

　　當然，這些都是很一般的方法，如果有問題相關領域知識，可以構建更好的圖，可以定義更好的距離方程，連線性以及邊權值。

　　接下來，我們介紹一些基於圖的半監督學習演算法，它們在損失函式和正則化的選擇上不同，為了簡單起見，我們假設標籤為{-1,1}。

MINCUT

　　我們將帶有正標籤的樣本作為源點（就好像流從這裡出發流經邊），相似的，負標籤樣本作為終點（流消失的點），目標是找到一個最小的邊集，使得刪除這些邊可以阻止所有從源點到終點的流，我們定義這樣的一組邊集叫做“cut”，割的大小用這些邊的權重和來定義。一旦圖被“割”開，與源點相連的點都被標記為正，反之為負。也就是說，我們想要找到這樣的一個作用在頂點上的函式f(x){-1,1}用來標記x的標籤，使得對於有標籤樣本來說f(xi)=yi，而且cut最小：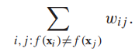

　　我們將最小割問題形式化為正則化風險最小化問題（合適的損失函式和正則化器）。對任何有標籤的頂點xi，f(xi)就是給定的標籤yi，可以用這樣一個損失函式來表示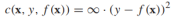： ，而正則化項則對應cut的大小，考慮到所有無標籤樣本的類別非負即正，cut的大小可以重寫為 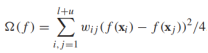。注意，當前的和是針對所有點對的，如果xi,xj不相連，wij=0。那麼最小割的正則化風險最小化問題可以寫作

 　　這是一個整數規劃問題，因此，最小割問題可以有許多多項式時間演算法可以解決。

　　這種形式的最小割問題可能存在多個最優解，比如下圖有兩個帶標籤點一正一負，每條邊有相同的權重，有6種最小割解決方案（移除任意一條邊即可）

HARMONIC FUNCTION

　　第二種基於圖的半監督學習演算法是調和函式，對於有標籤資料，調和函式的值為標籤值，對於無標籤資料，標籤值是權重平均：

 　　也就是說，無標籤頂點的值就是其鄰居頂點標籤值的權重平均，然後把它代入上面提到過的目標函式，並鬆弛f使它的值域為實數：

相當於求解：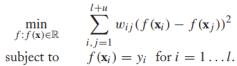

　　對f進行鬆弛使得f有一個閉式解，也就是說上述目標方程有全域性最優解，缺點是f(x)現在是一個[-1,1]的實數，並不能直接作為一個標籤。這可以通過設定閾值進行處理（如，如果f(x)>=0，預測標籤y=1，否則為-1）.

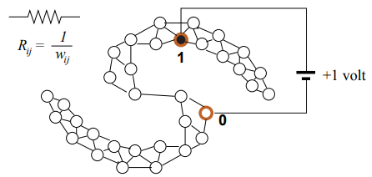
　　調和函式有許多有趣的解釋，比如，將圖看作一張電網，每一條邊的電阻為1/wij，有標籤的點連線到1v的電池，正標籤頂點連線電池正極，負標籤頂點連線電池負極，每個節點兩端的電壓就是調和函式值，如下圖所示：

　　調和函式也可以解釋為圖上的隨機遊走，想象一個粒子在頂點i上，那麼這個粒子會隨機走到下一個頂點j的概率是 ，隨機遊走以這種方式繼續，直到粒子到達一個有標記的頂點。那麼頂點i的調和函式值f(xi)就是粒子從i頂點出發最終走到一個正標籤的頂點的概率，如下圖所示：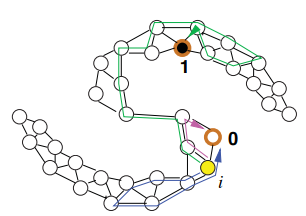

　　求解調和函式的過程是迭代的，初始的，我們設定：對於有標籤頂點，f(xi)=yi，對於無標籤頂點，f為任意值。每一輪迭代都用無標籤頂點鄰居的權重平均更新該無標籤頂點的標籤值：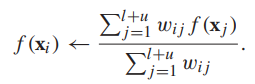

　　可以看出，無論初始值是多少，該迭代過程可以保證調和函式值收斂。這個過程也被稱為標籤傳播。

　　最後，我們來討論調和函式的閉式解：令W是一個（l+u）*（l+u）的權重矩陣，其中的元素是權重值wij。由於圖是無向的，所以W是一個對稱矩陣。它的元素是非負的， 是頂點i的加權度（與i相連的所有邊的和）。令D是（l+u）*（l+u）的對角矩陣，對角元素是Dii，定義非標準化的圖拉普拉斯矩陣L=D-W。

　　令 是所有頂點f值的向量，那麼正則化項可以寫作：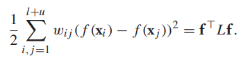

流形正則化

　　上面說的Mincut和harmonic function 都是轉換式的學習方法，它們無法直接一個之前沒有出現過的樣本的標籤，除非把該新樣本加入圖中成為新的節點，然後重新計算。如果我們要預測大量的資料，這顯然是不現實的，所以我們需要的是一種歸納的半監督學習演算法。而且，Mincut和harmonic function都規定有標籤資料的f(x)=y，在真實資料集中，可能存在標籤錯誤點或是噪聲點，我們希望f可以偶爾與給定標籤不同。

流形正則可以解決這兩個問題。這是一種歸納學習演算法，它在整個特徵空間上定義f： ，通過圖拉普拉斯變換，f被正則為對圖平滑。然而這個正則器只能控制f的值在（l+u）訓練集上的大小，為了防止f在訓練集以外的樣本上變化不平滑（泛化能力較差），有必要加第二個正則項，所以，流形正則的正則項可以寫作：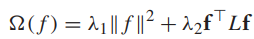

 　　那麼完整的流形正則目標函式可以寫作（損失函式可以根據實際情況進行替換）：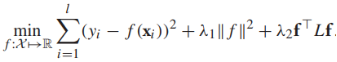

　　已經有有效的演算法找到最優的f。除了非標準化的圖拉普拉斯矩陣L之外，也常常使用標準化的圖拉普拉斯矩陣：

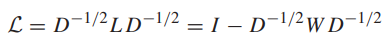
　　這使得正則項有一些不同

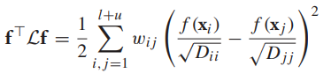
The Assumption of graph-based method

　　基於圖的半監督學習假設：圖的標籤是“平滑”的，標籤在圖上的變化非常緩慢，也就是說如果兩個樣本在圖上有強邊相連，它們的標籤很大概率相同。平滑的概念可以用譜圖理論來精確表示。向量φ是方陣A的一個特徵向量如果Aφ=λφ（λ是特徵向量對應的特徵值）。如果φ是一個特徵向量，cφ（c!=0）也是一個特徵向量。但是我們關注單位特徵向量||φ||=1，普圖理論涉及一個圖的特徵向量和特徵值，用拉普拉斯矩陣L來表示。我們將分析非正則化拉普拉斯矩陣L，它有如下特性：

• L有（l+u）個特徵值（可重複）和對應的特徵向量 ，這些對叫做圖譜，特徵向量是正交的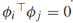 （i!=j）。
• 拉普拉斯矩陣可分解為外積的加權和:
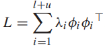
• 特徵值是非負實數，

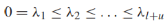
• 圖有k個連通分量當且僅當 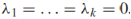對應的特徵向量在單個連通分量上是常數或0。

小結：

　　本章主要介紹了使用圖的相關知識解決半監督學習的問題。我們討論的幾種演算法都基於預測的標籤在圖上是平滑的，並介紹了一些關於譜圖理論的概念來證明這些方法。在之後的文章中，我們將討論半監督支援向量機。

希望大家多多支援我的公眾號，掃碼關注，我們一起學習，一起進步~